随机游走
在本节中,我们将使用 Python 生成随机漫步的数据,然后使用 Matplotlib 创建该数据的可视化表示。随机行走是由一系列简单的决定所决定的路径,其中每一个决定都完全是偶然的。你可以把随机漫步想象成一只混乱的蚂蚁,如果它每一步都朝着随机的方向走,那么它所走的路径就是随机漫步。
随机行走在自然界、物理学、生物学、化学和经济学中都有实际应用。例如,漂浮在水滴上的花粉粒会在水面上移动,因为它不断受到水分子的推动。水滴中的分子运动是随机的,因此花粉粒在水面上的运动轨迹就是随机行走。我们接下来要编写的代码模拟了现实世界中的许多情况。
创建 RandomWalk 类
为了创建随机行走,我们将创建一个 RandomWalk 类,它将随机决定行走的方向。该类需要三个属性:一个变量用于跟踪行走中的点数,两个列表用于存储行走中每个点的 x 坐标和 y 坐标。
我们只需要 RandomWalk 类的两个方法:__init__() 方法和 fill_walk(),后者将计算行走过程中的点。让我们从 __init__() 方法开始:
from random import choice
class RandomWalk:
"""A class to generate random walks."""
def __init__(self, num_points=5000):
"""Initialize attributes of a walk."""
self.num_points = num_points
# All walks start at (0, 0).
self.x_values = [0]
self.y_values = [0]为了做出随机决定,我们会将可能的移动存储在一个列表中,然后使用 choice() 函数(来自随机模块)来决定每次走一步时要走哪一步❶。我们将行走中的默认点数设置为 5000,这个数字足够大,可以产生一些有趣的模式,但又足够小,可以快速产生行走❷。然后,我们制作两个列表来保存 x 值和 y 值,每次行走都从点 (0, 0) ❸ 开始。
选择方向
我们将使用 fill_walk() 方法来确定行走过程中的完整点序列。将此方法添加到 random_walk.py 中:
def fill_walk(self):
"""Calculate all the points in the walk."""
# Keep taking steps until the walk reaches the desired length.
while len(self.x_values) < self.num_points: (1)
# Decide which direction to go, and how far to go.
x_direction = choice([1, -1]) (2)
x_distance = choice([0, 1, 2, 3, 4])
x_step = x_direction * x_distance (3)
y_direction = choice([1, -1])
y_distance = choice([0, 1, 2, 3, 4])
y_step = y_direction * y_distance (4)
# Reject moves that go nowhere.
if x_step == 0 and y_step == 0: (5)
continue
# Calculate the new position.
x = self.x_values[-1] + x_step (6)
y = self.y_values[-1] + y_step
self.x_values.append(x)
self.y_values.append(y)我们首先建立一个循环,运行直到用正确的点数 ❶ 填充行走。fill_walk() 的主要部分告诉 Python 如何模拟四个随机决定:行走是向右还是向左?会朝那个方向走多远?是向上还是向下?会朝那个方向走多远?
我们使用 choice([1, -1]) 为 x_direction 选择一个值,返回 1 表示向右移动,返回 -1 表示向左❷移动。接下来,choice([0, 1, 2, 3, 4]) 会随机选择一个向该方向移动的距离。我们将这个值赋值给 x_distance。0 的加入允许步长只沿一个轴移动。
我们用移动方向乘以选择的距离❸❹,来确定 x 和 y 方向上每一步的长度。x_step 的正值表示向右移动,负值表示向左移动,0 表示垂直移动。y_step 的正值表示向上移动,负值表示向下移动,0 表示水平移动。如果 x_step 和 y_step 的值都为 0,则行走没有任何进展;出现这种情况时,我们将继续循环 ❺。
为了得到下一个行走的 x 值,我们将 x_step 中的值与 x_values ❻ 中存储的最后一个值相加,并对 y 值做同样的处理。得到新点坐标后,我们将其添加到 x_values 和 y_values 中。
绘制随机游走
以下是绘制行走中所有点的代码:
import matplotlib.pyplot as plt
from random_walk import RandomWalk
# Make a random walk.
rw = RandomWalk() (1)
rw.fill_walk()
# Plot the points in the walk.
plt.style.use('classic')
fig, ax = plt.subplots()
ax.scatter(rw.x_values, rw.y_values, s=15) (2)
ax.set_aspect('equal') (3)
plt.show()首先,我们导入 pyplot 和 RandomWalk。然后,我们创建一个随机行走并将其赋值给 rw ❶,同时确保调用 fill_walk()。为了使行走可视化,我们将行走的 x 值和 y 值输入 scatter() 并选择合适的点尺寸❷。默认情况下,Matplotlib 会独立缩放每个坐标轴。但这种方法会在水平或垂直方向上拉伸大多数行走。在这里,我们使用 set_aspect() 方法指定两个坐标轴的刻度线间距❸ 一致。
图 15-9 显示了 5000 个点的结果图。本节中的图片省略了 Matplotlib 的查看器,但运行 rw_visual.py 时仍可看到。
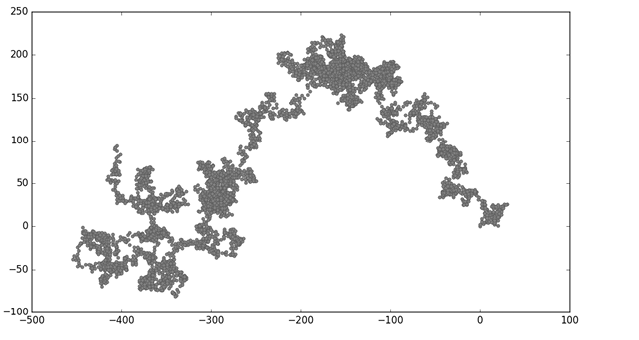
生成多个随机游走
每一次随机行走都是不同的,探索可以生成的各种模式也很有趣。使用前面的代码进行多次随机行走而无需多次运行程序的一种方法是将其封装在一个 while 循环中,就像下面这样:
import matplotlib.pyplot as plt
from random_walk import RandomWalk
# Keep making new walks, as long as the program is active.
while True:
# Make a random walk.
--snip--
plt.show()
keep_running = input("Make another walk? (y/n): ")
if keep_running == 'n':
break这段代码会生成一个随机漫步,将其显示在 Matplotlib 的查看器中,并在查看器打开时暂停。关闭查看器时,系统会询问您是否要生成另一个随机游走。如果您生成了几条漫步线,您应该会看到有的漫步线停留在起点附近,有的漫步线主要朝一个方向游走,有的漫步线有细长的部分连接着较大的点群,还有许多其他类型的漫步线。想结束程序时,按 N。
塑造步行风格
在本节中,我们将定制我们的绘图,以强调每次行走的重要特征,并淡化分散注意力的元素。为此,我们要确定要强调的特征,如步行开始的位置、结束的位置和路径。接下来,我们确定要淡化的特征,如刻度线和标签。这样做的结果应该是一个简单的可视化表示,能够清楚地传达每次随机游走的路径。
为点着色
我们将使用颜色图来显示行走过程中各点的顺序,并移除每个点的黑色轮廓,这样点的颜色就会更加清晰。要根据各点在行走过程中的位置给它们着色,我们需要向 c 参数传递一个包含各点位置的列表。因为点是按顺序绘制的,所以这个列表只包含 0 到 4999 之间的数字:
--snip--
while True:
# Make a random walk.
rw = RandomWalk()
rw.fill_walk()
# Plot the points in the walk.
plt.style.use('classic')
fig, ax = plt.subplots()
point_numbers = range(rw.num_points)
ax.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues,edgecolors='none', s=15)
ax.set_aspect('equal')
plt.show()
--snip--我们使用 range() 生成一个数字列表,该列表中的数字等于行走过程中的点数 ❶。我们将这个列表赋值给 point_numbers,用来设置行走过程中每个点的颜色。我们将 point_numbers 传递给 c 参数,使用 Blues colormap,然后传递 edgecolors='none' 以去除每个点周围的黑色轮廓。结果是一幅从浅蓝到深蓝的曲线图,准确显示了行走从起点到终点的过程。如图 15-10 所示。
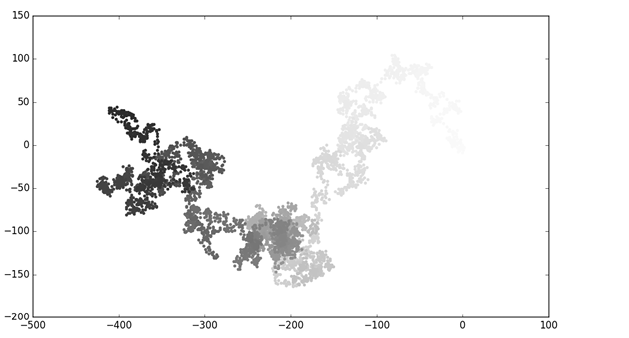
绘制起点和终点图
除了给点着色以显示其在行走过程中的位置外,我们还可以看到每次行走的确切起点和终点。为此,我们可以在绘制完主序列后,单独绘制第一个点和最后一个点。我们将把终点放大,并用不同的颜色来突出它们:
--snip--
while True:
--snip--
ax.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolors='none', s=15)
ax.set_aspect('equal')
# Emphasize the first and last points.
ax.scatter(0, 0, c='green', edgecolors='none', s=100)
ax.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none',s=100)
plt.show()
--snip--为了显示起点,我们将点(0,0)绘制成绿色,且大小(s=100)大于其他点。为了标记终点,我们将最后一个 x 值和 y 值也标为红色,大小为 100。确保在调用 plt.show() 之前插入此代码,这样起点和终点就会绘制在所有其他点的上方。
运行这段代码后,您应该可以准确地找到每条路径的起点和终点。如果这些终点不够突出,可以调整它们的颜色和大小,直到它们足够突出为止。
清理轴
让我们移除图中的坐标轴,这样它们就不会干扰每次行走的路径。下面是隐藏坐标轴的方法:
--snip--
while True:
--snip--
ax.scatter(rw.x_values[-1], rw.y_values[-1], c='red', edgecolors='none', s=100)
# Remove the axes.
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
--snip--为了修改坐标轴,我们使用 ax.get_xaxis() 和 ax.get_yaxis() 方法获取每个坐标轴,然后使用 set_visible() 方法链使每个坐标轴不可见。在继续使用可视化的过程中,你会经常看到这种方法链来定制可视化的不同方面。
现在运行 rw_visual.py,你会看到一系列没有坐标轴的曲线图。
添加绘图点
让我们增加点的数量,以便获得更多数据。为此,我们可以在创建 RandomWalk 实例时增加 num_points 的值,并在绘制曲线图时调整每个点的大小:
--snip--
while True:
# Make a random walk.
rw = RandomWalk(50_000)
rw.fill_walk()
# Plot the points in the walk.
plt.style.use('classic')
fig, ax = plt.subplots()
point_numbers = range(rw.num_points)
ax.scatter(rw.x_values, rw.y_values, c=point_numbers, cmap=plt.cm.Blues, edgecolors='none', s=1)
--snip--本例创建了一个包含 50,000 个点的随机漫步,并以 s=1 的大小绘制每个点。如图 15-11 所示,绘制出的漫步图飘渺如云。我们从简单的散点图中创造出了一件艺术品!
用这段代码做个实验,看看在系统开始明显变慢或曲线图失去视觉吸引力之前,你能增加多少随机游走的点数。

改变尺寸以填充屏幕
如果可视化能很好地显示在屏幕上,就能更有效地传达数据的模式。要使绘图窗口更适合屏幕,可以调整 Matplotlib 输出的大小。这可以通过调用 subplots() 来实现:
fig, ax = plt.subplots(figsize=(15, 9))创建绘图时,可以向 subplots() 传递 figsize 参数,设置图形的大小。figsize 参数包含一个元组,它告诉 Matplotlib 绘图窗口的尺寸(以英寸为单位)。
Matplotlib 假定屏幕分辨率为每英寸 100 像素;如果这段代码不能提供准确的绘图尺寸,请根据需要调整数字。如果您知道系统的分辨率,也可以使用 dpi 参数将分辨率传递给 subplots():
fig, ax = plt.subplots(figsize=(10, 6), dpi=128)这将有助于最有效地利用屏幕上的可用空间。