浮点数

Go 语言提供了两种精度的浮点数，float32 和 float64 。它们的算术规范由IEEE754浮点数国际标准定义，该浮点数规范被所有现代的 CPU 支持。

这些浮点数类型的取值范围可以从很微小到很巨大。浮点数的范围极限值可以在 math 包找到。常量 math.MaxFloat32 表示 float32 能表示的最大数值，大约是 3.4e38；对应的 math.MaxFloat64 常量大约是 1.8e308 。它们分别能表示的最小值近似为 1.4e-45 和 4.9e-324 。

一个 float32 类型的浮点数可以提供大约 6 个十进制数的精度，而 float64 则可以提供约 15 个十进制数的精度；通常应该优先使用 float64 类型，因为 float32 类型的累计计算误差很容易扩散，并且 float32 能精确表示的正整数并不是很大（译注：因为 float32 的有效bit位只有 23 个，其它的bit位用于指数和符号；当整数大于23bit能表达的范围时，float32 的表示将出现误差）：

var f float32 = 16777216 // 1 << 24
fmt.Println(f == f+1)    // "true"!

浮点数的字面值可以直接写小数部分，像这样：

const e = 2.71828 // (approximately)

小数点前面或后面的数字都可能被省略（例如 .707 或 1. ）。很小或很大的数最好用科学计数法书写，通过 e 或 E 来指定指数部分：

const Avogadro = 6.02214129e23  // 阿伏伽德罗常数
const Planck   = 6.62606957e-34 // 普朗克常数

用 Printf 函数的 %g 参数打印浮点数，将采用更紧凑的表示形式打印，并提供足够的精度，但是对应表格的数据，使用 %e（带指数）或 %f 的形式打印可能更合适。所有的这三个打印形式都可以指定打印的宽度和控制打印精度。

for x := 0; x < 8; x++ {
    fmt.Printf("x = %d e^x = %8.3f\n", x, math.Exp(float64(x)))
}

上面代码打印 e 的幂，打印精度是小数点后三个小数精度和 8 个字符宽度：

x = 0       e^x =    1.000
x = 1       e^x =    2.718
x = 2       e^x =    7.389
x = 3       e^x =   20.086
x = 4       e^x =   54.598
x = 5       e^x =  148.413
x = 6       e^x =  403.429
x = 7       e^x = 1096.633

math 包中除了提供大量常用的数学函数外，还提供了 IEEE754 浮点数标准中定义的特殊值的创建和测试：正无穷大和负无穷大，分别用于表示太大溢出的数字和除零的结果；还有 NaN 非数，一般用于表示无效的除法操作结果 0/0 或 Sqrt(-1) 。

var z float64
fmt.Println(z, -z, 1/z, -1/z, z/z) // "0 -0 +Inf -Inf NaN"

函数 math.IsNaN 用于测试一个数是否是非数 NaN ，math.NaN 则返回非数对应的值。虽然可以用 math.NaN 来表示一个非法的结果，但是测试一个结果是否是非数 NaN 则是充满风险的，因为 NaN 和任何数都是不相等的（译注：在浮点数中，NaN、正无穷大和负无穷大都不是唯一的，每个都有非常多种的bit模式表示）：

nan := math.NaN()
fmt.Println(nan == nan, nan < nan, nan > nan) // "false false false"

如果一个函数返回的浮点数结果可能失败，最好的做法是用单独的标志报告失败，像这样：

func compute() (value float64, ok bool) {
    // ...
    if failed {
        return 0, false
    }
    return result, true
}

接下来的程序演示了通过浮点计算生成的图形。它是带有两个参数的 z = f(x, y) 函数的三维形式，使用了可缩放矢量图形（ SVG ）格式输出，SVG 是一个用于矢量线绘制的 XML 标准。图3.1显示了 sin(r)/r 函数的输出图形，其中 r 是 sqrt(x*x+y*y) 。

ch3/surface

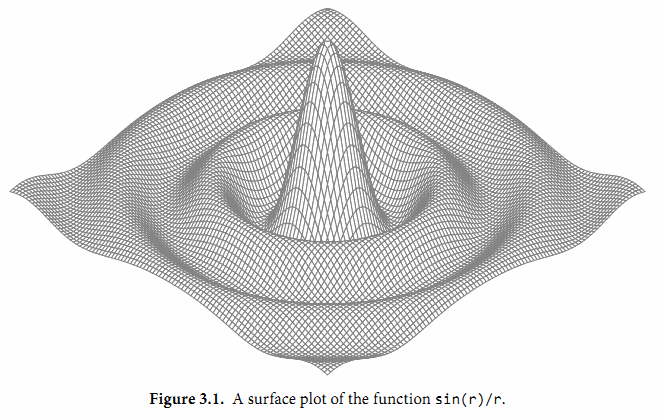
Unresolved include directive in modules/ROOT/pages/ch3/ch3-02.adoc - include::example$/ch3/surface/main.go[]

要注意的是 corner 函数返回了两个结果，分别对应每个网格顶点的坐标参数。

要解释这个程序是如何工作的需要一些基本的几何学知识，但是我们可以跳过几何学原理，因为程序的重点是演示浮点数运算。程序的本质是三个不同的坐标系中映射关系，如图3.2所示。第一个是 100x100 的二维网格，对应整数坐标 (i,j)，从远处的 (0,0) 位置开始。我们从远处向前面绘制，因此远处先绘制的多边形有可能被前面后绘制的多边形覆盖。

第二个坐标系是一个三维的网格浮点坐标 (x,y,z) ，其中 x 和 y 是 i 和 j 的线性函数，通过平移转换为网格单元的中心，然后用 xyrange 系数缩放。高度 z 是函数 f(x,y) 的值。

第三个坐标系是一个二维的画布，起点 (0,0) 在左上角。画布中点的坐标用 (sx,sy) 表示。我们使用等角投影将三维点 (x,y,z) 投影到二维的画布中。

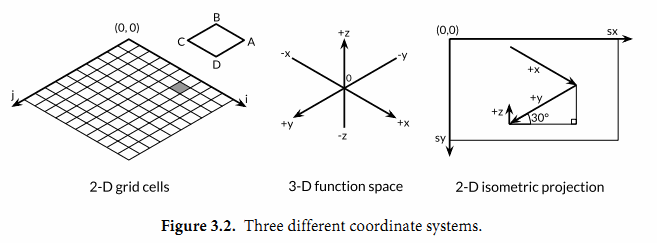
画布中从远处到右边的点对应较大的 x 值和较大的 y 值。并且画布中 x 和 y 值越大，则对应的 z 值越小。 x 和 y 的垂直和水平缩放系数来自 30 度角的正弦和余弦值。z的缩放系数 0.4 ，是一个任意选择的参数。

对于二维网格中的每一个网格单元，main 函数计算单元的四个顶点在画布中对应多边形ABCD 的顶点，其中 B 对应 (i,j) 顶点位置，A、C 和 D 是其它相邻的顶点，然后输出 SVG 的绘制指令。

练习 3.1：如果 f 函数返回的是无限制的 float64 值，那么 SVG 文件可能输出无效的多边形元素（虽然许多 SVG 渲染器会妥善处理这类问题）。修改程序跳过无效的多边形。

练习 3.2：试验 math 包中其他函数的渲染图形。你是否能输出一个 egg box、moguls 或 a saddle 图案?

练习 3.3：根据高度给每个多边形上色，那样峰值部将是红色（#ff0000），谷部将是蓝色（#0000ff）。

练习 3.4：参考1.7节 Lissajous 例子的函数，构造一个 web 服务器，用于计算函数曲面然后返回 SVG 数据给客户端。服务器必须设置 Content-Type 头部：

w.Header().Set("Content-Type", "image/svg+xml")

（这一步在 Lissajous 例子中不是必须的，因为服务器使用标准的 PNG 图像格式，可以根据前面的 512 个字节自动输出对应的头部。）允许客户端通过 HTTP 请求参数设置高度、宽度和颜色等参数。