理解大 O 符号

大 O 符号对于算法分析非常重要。我们需要扎实地理解这个符号，以及今后如何使用它。我们将在本节中讨论大 O 符号。

我们查找图书并放置图书的算法有 n 个项目。对于第一次图书搜索，它将在最坏的情况下比较 n 本图书。如果我们说时间复杂度为 T，那么对于第一本书，时间复杂度将为：

由于我们要从列表中删除已建立的图书，因此列表的大小现在是 n-1。对于第二次图书搜索，在最坏的情况下，它将比较 n-1 本图书。那么对于第二本书，时间复杂度将为 n-1。综合这两个时间复杂度，前两本书的时间复杂度将是：

如果我们继续这样，在 n-1 步之后，最后一本书搜索将只剩下 1 本书可供比较。 因此，总复杂度将如下所示：

现在我们来看看前面的数列，是不是很眼熟？如图所示，它也被称为 n 个数之和的等式：

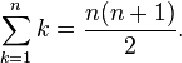
因此，我们可以写道：

或者：

为了进行渐近分析，我们忽略了低阶项和常数乘数。因为我们有 n²，所以可以很容易地忽略这里的 n。此外，1/2 常乘数也可以忽略。现在，我们可以用大 O 符号将时间复杂度表示为 n 的平方阶次：

在整本书中，我们将使用大 O 符号来描述算法或操作的复杂性。下面是一些常用的大 O 符号：