了解合并排序
我们已经知道,合并排序应用了分而治之的方法来解决排序问题,因此我们需要找出两个过程来解决这个问题。第一种是将问题集划分为足够小的问题,以便轻松解决,然后将这些结果合并起来。在这里,我们将采用递归方法来完成分而治之的部分。下图展示了如何采用分而治之的方法。现在,我们将考虑一个由 20、45、93、67、97、52、88、33 组成的较小的数字列表来解释除法与征服部分:
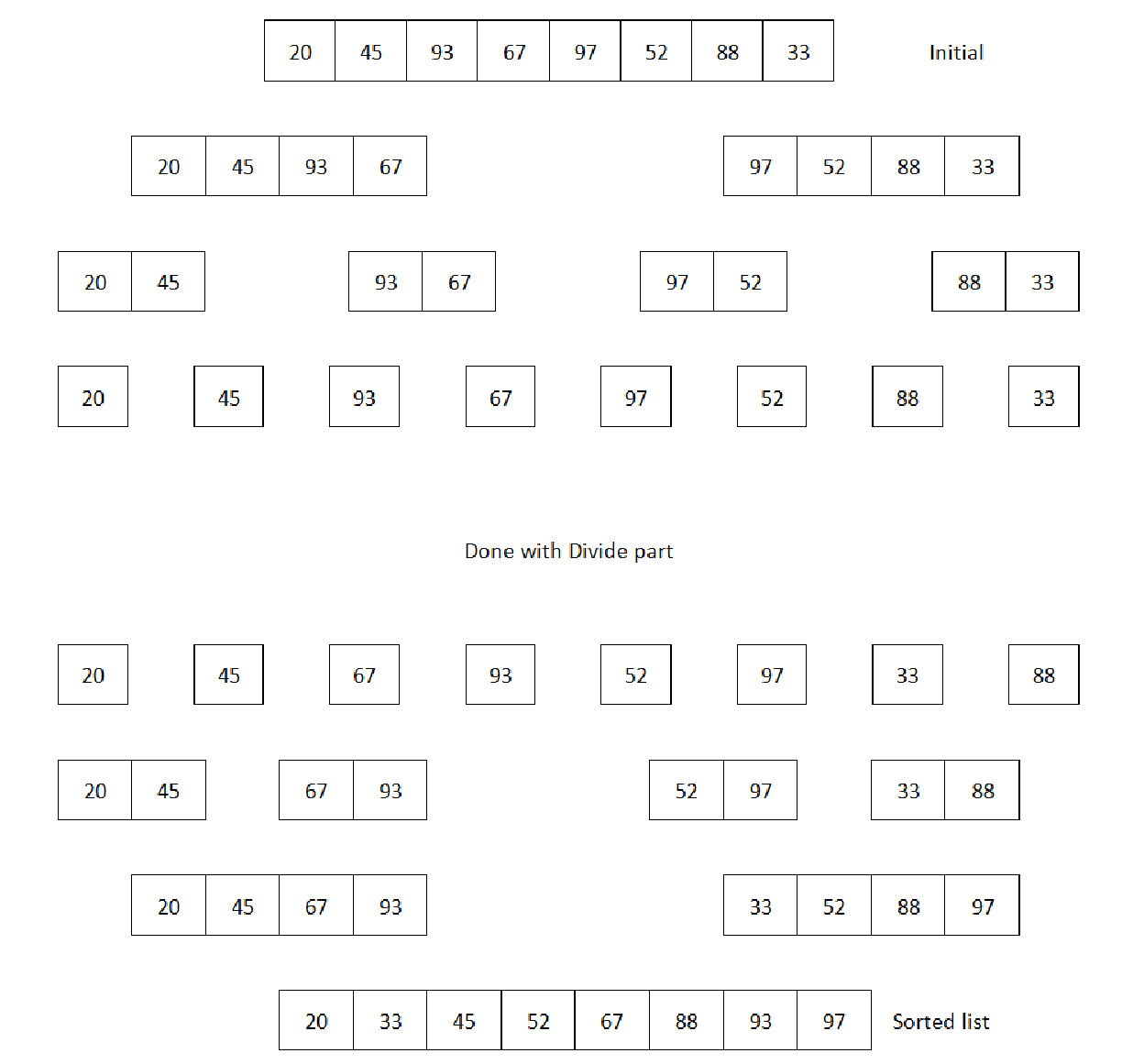
根据前面的图片,我们现在可以开始准备我们的伪代码,它将包括两个部分—分而治之。下面是实现这一目标的伪代码:
func mergesort(A : array of sortable items):
n = length(A)
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )
l2 = mergesort( l2 )
return merge( l1, l2 )
end func
func merge( a: array, b : array )
c = array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
end while
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
end while
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
return c
end while
end func伪代码的第一部分显示了分割过程。我们分割了数组中的条目,直到它的大小达到 1。 然后,我们开始使用 merge 函数合并结果。在合并函数中,我们用一个数组来存储合并后的结果。正因为如此,合并排序的空间复杂度实际上高于我们目前看到的其他算法。现在,让我们开始编码,用 PHP 实现这个伪代码。
实现合并排序
我们将首先编写分割部分,然后编写合并或征服部分。PHP 有一些内置函数来分割数组。我们将使用 array_slice 函数进行分割。代码如下:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-06.adoc - include::example$Chapter07/7.php[]从代码中我们可以看到,我们以递归方式拆分数组,直到数组大小变为 1。当数组大小为 1 时,我们开始向后合并,就像上一张图片一样。下面是合并函数的代码,它将接收两个数组,并按照我们的伪代码将它们合并为一个数组:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-06.adoc - include::example$Chapter07/7.php[]现在代码已经完成,我们合并了提供的两个数组,并将合并结果返回给 mergeSort 函数。我们刚刚以递归方式解决了问题。如果运行以下代码,您将得到一个升序排列的项目列表:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-06.adoc - include::example$Chapter07/7.php[]现在,让我们来探讨一下合并排序的复杂性。
归并排序的复杂度
由于合并排序遵循分而治之的方法,因此我们必须解决这两个复杂问题。对于一个 n 大小的数组,我们首先需要将数组分成两半,然后合并,得到一个 n 大小的数组。这可以用 \$T(n)\$ 来表示,即:
T(n) = T(n/2) + T(n/2) + n , for N>1 with T(1) = 0
= 2 T(n/2)+n
T(n)/n = 2 T(n/2)/n + 1 // divide both side by n
= T(n/2)/(n/2) + 1
= T(n/4)/(n/4) + 1+ 1 // telescoping
= T(n/8)/(n/8) + 1+ 1 + 1 // again telescoping
= ......
= T(n/n)/(n/n) + 1 + 1 + 1 + ....... + 1
= log (n) // since T(1) = 0
So T(n) = n log (n) // multiply both side with n因此,合并排序的复杂度为 \$O(nlog(n))\$。下面是合并排序的复杂度图:
最好时间复杂度 |
\$Ω(nlog(n))\$ |
最坏时间复杂度 |
\$O(nlog(n))\$ |
平均时间复杂度 |
\$Θ(nlog(n))\$ |
空间复杂度(最差情况) |
\$O(n)\$ |