使用 Bellman-Ford 算法查找最短路径
尽管 Dijkstra 算法是用于寻找单源最短路径的最流行、最高效的算法,但它有一个问题没有解决。如果图中存在负循环,Dijkstra 算法就无法检测到负循环,因此也就无法运行。负循环是指循环中所有边的总和为负数的循环。如果图中包含负循环,那么就无法找到最短路径,因此我们在寻找最短路径时必须解决这个问题。这就是我们使用 Bellman-Ford 算法的原因,尽管它比 Dijkstra 算法慢。
下面是最短路径的贝尔曼-福特算法的算法伪码:
function BellmanFord(list vertices, list edges, vertex source)
// This implementation takes a vertex source
// and fills distance array with shortest-path information
// Step 1: initialize graph
for each vertex v in vertices:
if v is source
distance[v] := 0
else
distance[v] := infinity
// Step 2: relax edges repeatedly
for i from 1 to size(vertices)-1:
for each edge (u, v) with weight w in edges:
if distance[u] + w < distance[v]:
distance[v] := distance[u] + w
// Step 3: check for negative-weight cycles
for each edge (u, v) with weight w in edges:
if distance[u] + w < distance[v]:
error "Graph contains a negative-weight cycle"我们可以看到,Bellman-Ford 算法在寻找节点间的最短路径时,也会考虑边沙顶点。这就是所谓的松弛过程,在 Dijkstra 算法中也有使用。图算法中的松弛过程指的是更新与顶点 V 相连的所有顶点的成本,如果这些成本会因为包含经过 V 的路径而得到改善的话。简单地说,松弛过程就是试图降低使用另一个顶点到达一个顶点的成本。现在,我们将在与 Dijkstra 算法相同的图中实现这一算法。唯一不同的是,这里我们将使用数字标签来表示节点和顶点:
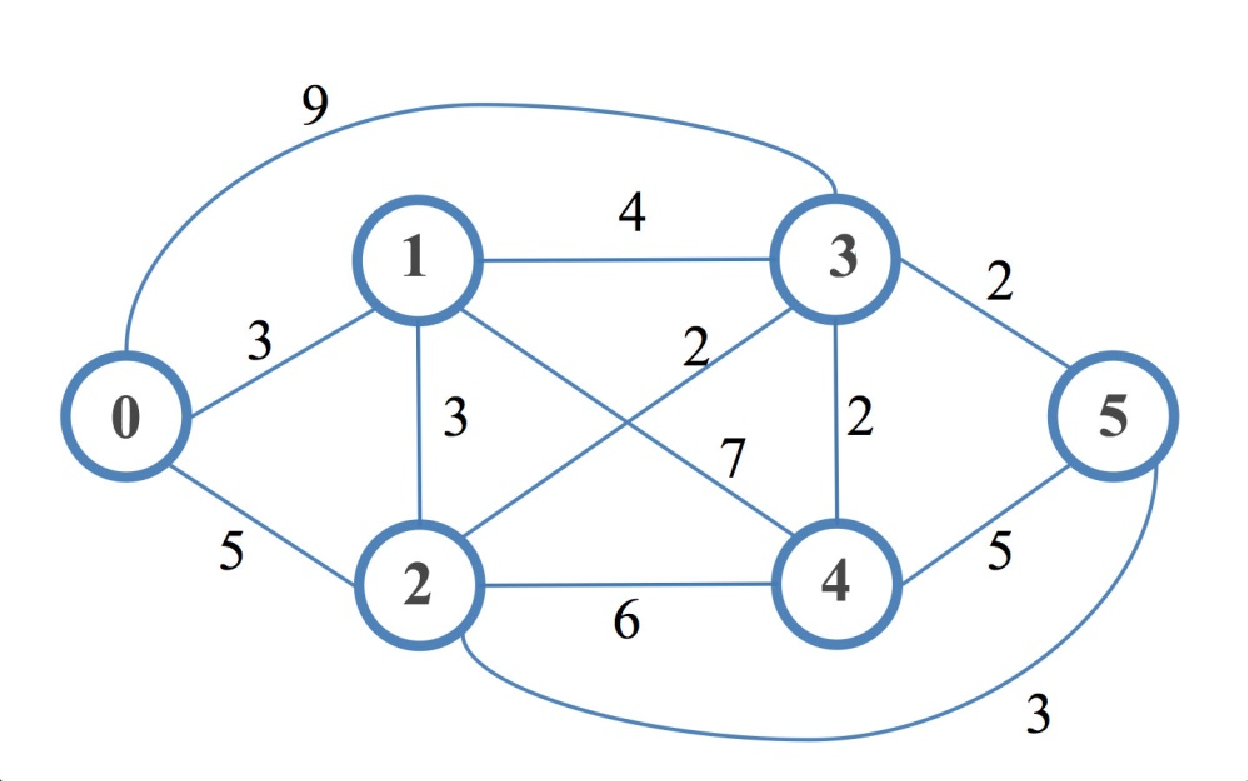
现在该用邻接矩阵格式来表示图了。下面是 PHP 中的矩阵:
$graph = [
0 => [0, 3, 5, 9, 0, 0],
1 => [3, 0, 3, 4, 7, 0],
2 => [5, 3, 0, 2, 6, 3],
3 => [9, 4, 2, 0, 2, 2],
4 => [0, 7, 6, 2, 0, 5],
5 => [0, 0, 3, 2, 5, 0]
];之前,我们用 0 表示两个顶点之间没有边。如果我们在这里也这样做,那么在两条边之间取一个最小值,其中一个代表 0,在松弛过程中将总是得到一个 0,这实际上意味着两个顶点之间没有连接。因此,我们必须选择一个更大的数字来表示不存在的边。我们可以使用 PHP 的 MAX_INT_VALUE 常量来表示这些边,这样就不会考虑这些不存在的边了。这就是我们的新图形表示法:
Unresolved include directive in modules/ROOT/pages/ch09/ch9-07.adoc - include::example$Chapter09/6.php[]现在,让我们来编写 Bellman-Ford 算法的实现。我们将使用在伪代码中定义的相同方法:
Unresolved include directive in modules/ROOT/pages/ch09/ch9-07.adoc - include::example$Chapter09/6.php[]与 Dijkstra 算法不同的是,我们没有跟踪前人。我们在松弛过程中考虑的是距离。由于我们使用的是 PHP 中整数的最大值,因此会自动排除选择一条值为 0 的不存在边作为最小路径的可能性。实现的最后一部分是检测给定图中的任何负循环,并在这种情况下返回一个空数组:
Unresolved include directive in modules/ROOT/pages/ch09/ch9-07.adoc - include::example$Chapter09/6.php[]输出结果如下,显示了从源节点到其他节点的最短路径距离:
distance from 0 to 0 is 0
distance from 0 to 1 is 3
distance from 0 to 2 is 5
distance from 0 to 3 is 7
distance from 0 to 4 is 9
distance from 0 to 5 is 8贝尔曼-福特算法的运行时间复杂度为 \$O (V,E)\$。