不同类型的树结构
编程世界中有许多类型的树形数据结构。我们将在此探讨一些最常用的树形结构。
二叉搜索树
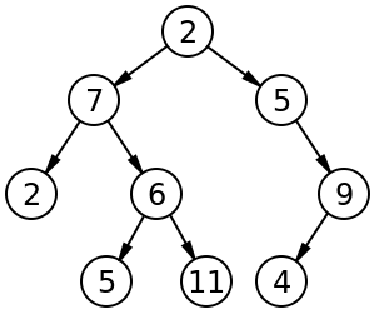
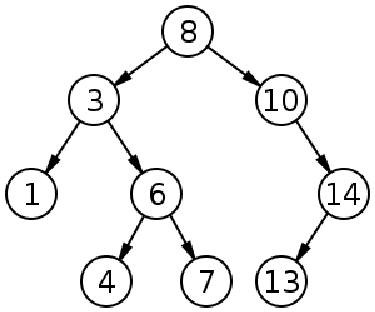
二叉搜索树(BST)是一种特殊的二叉树,其节点以排序方式存储。它的排序方式是,在任何给定的点上,节点值必须大于或等于左侧子节点值,小于右侧子节点值。每个节点都必须满足这一属性,才能将其视为二叉搜索树。由于节点是按特定顺序排列的,因此二进制搜索算法可以在对数时间内搜索 BST 中的项目。它总是优于线性搜索,后者需要 \$O(n)\$ 时间,我们将在下一章探讨它。下面是二叉搜索树的一个示例:
自平衡二叉搜索树
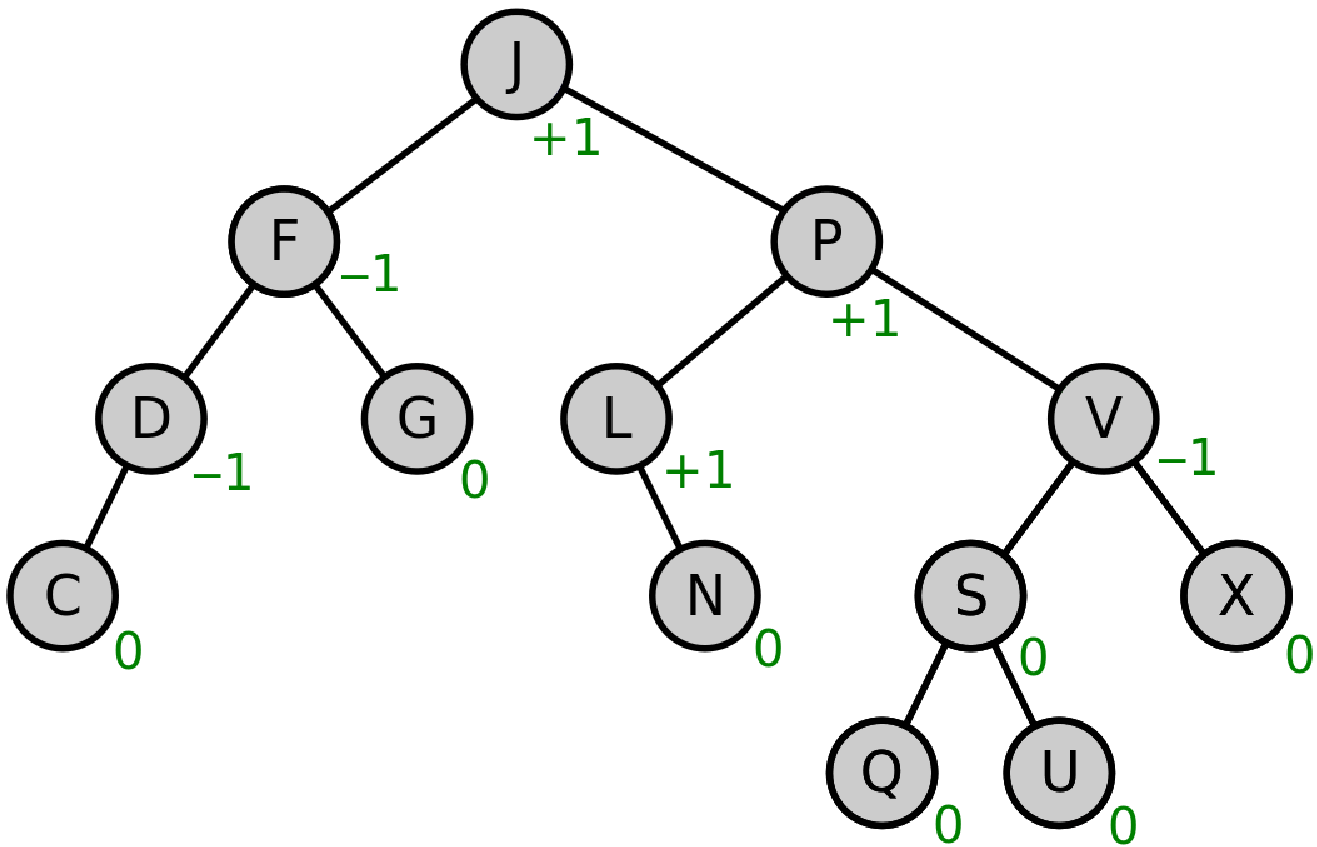
自平衡二叉搜索树或高度平衡二叉搜索树是一种特殊类型的二叉搜索树,它试图通过自动调整来始终保持树的高度或层数尽可能小。例如,下图左边是一棵二叉搜索树,右边是一棵自平衡二叉搜索树:
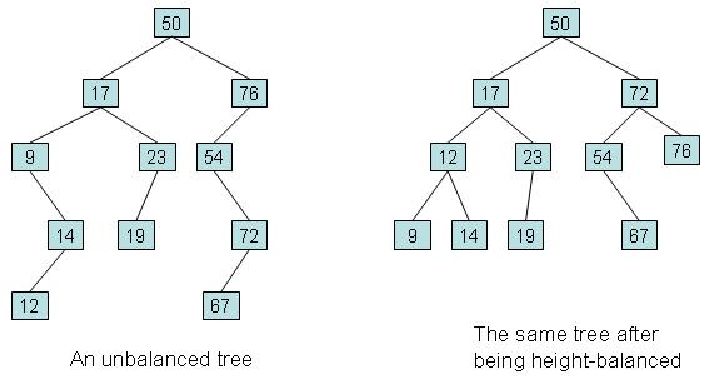
高度平衡二叉树总是更好,因为与普通二叉树相比,它有助于更快地进行搜索操作。自平衡或高度平衡二叉搜索树有不同的实现方式。以下是一些常用的实现方法:
-
AA 树
-
AVL 树
-
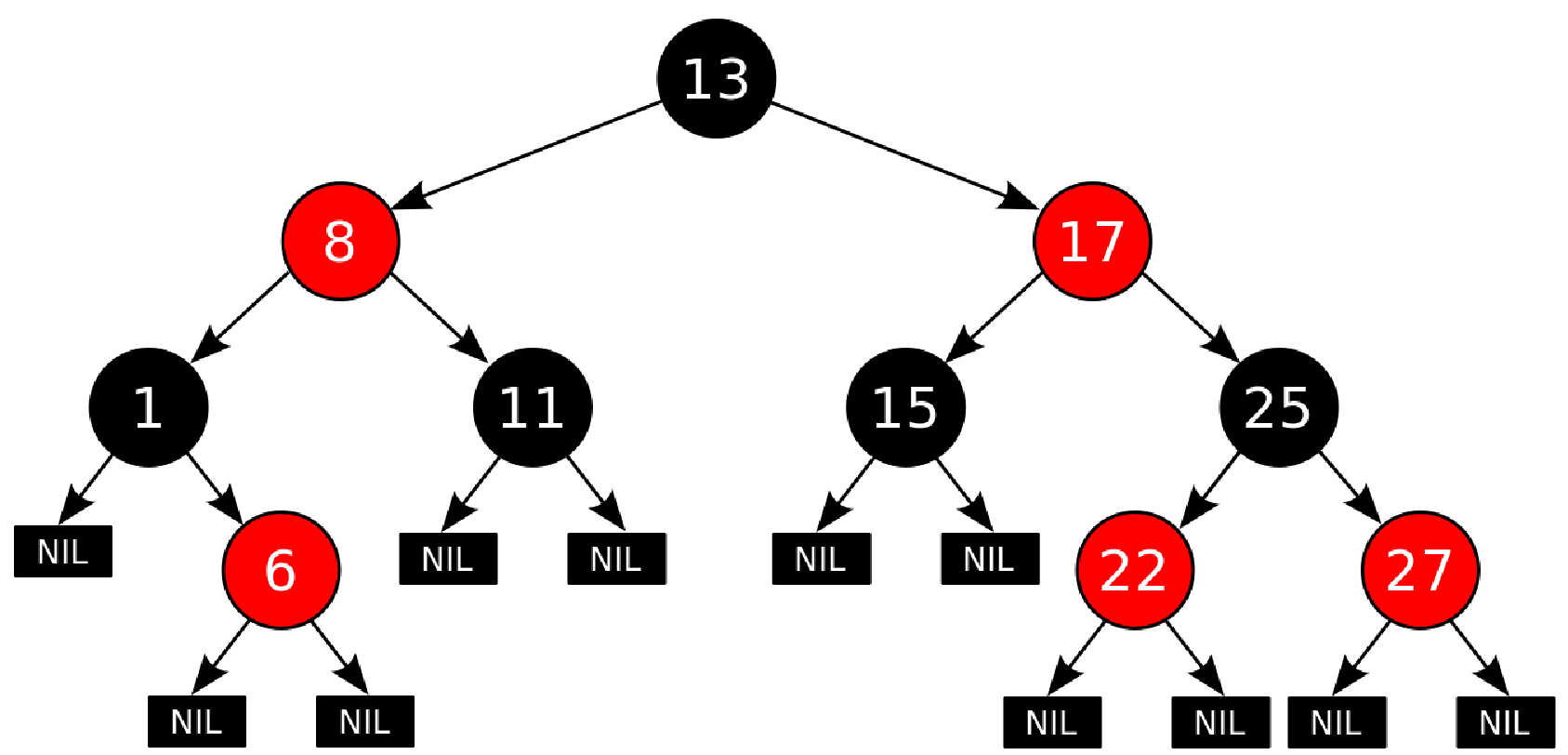
红黑树
-
替罪羊树
-
八字树
-
2-3 树
-
Treap
我们将在下面的部分中讨论一些高度平衡的树。