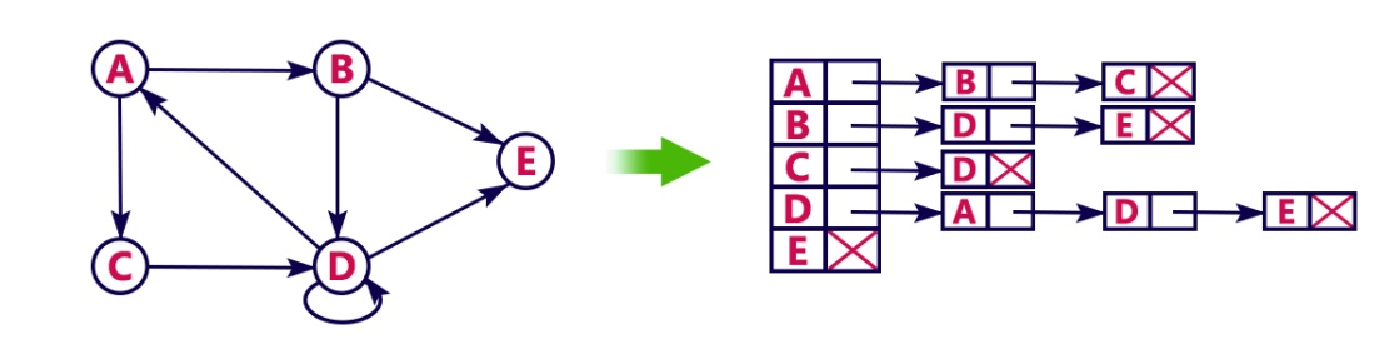
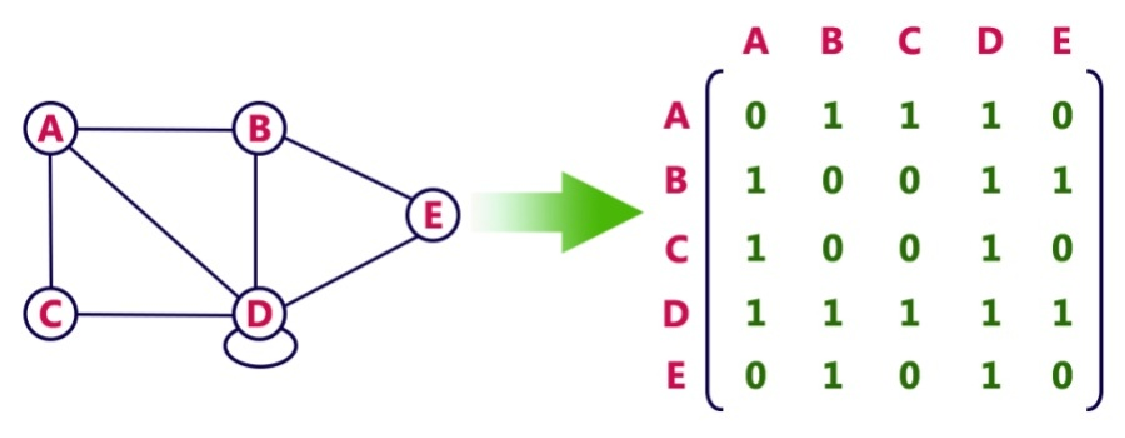
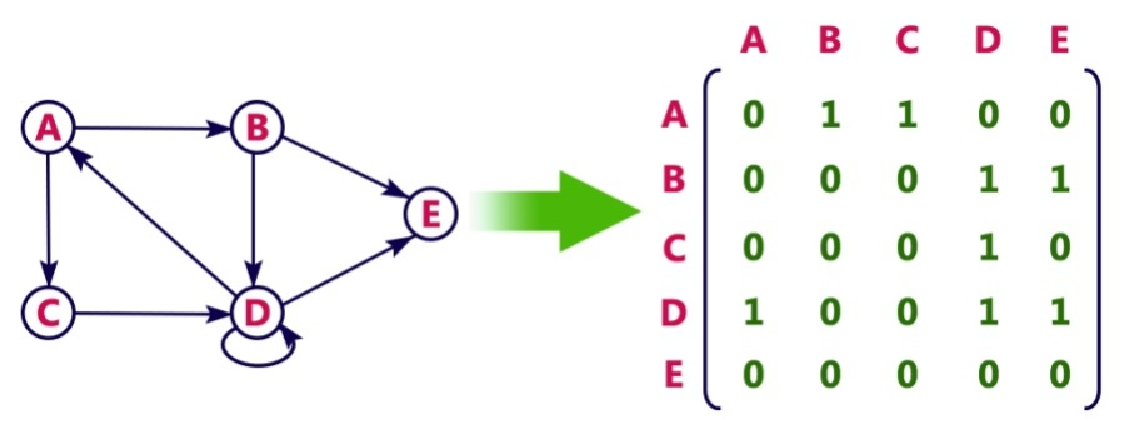
图表类型
根据绘制或表示方式的不同,有不同类型的图表可供选择。每种类型的图形都有不同的行为和用途。我们将重点介绍四种主要的图形类型。
有向图
如果一个图只包含有向边,那么这个图就被称为有向图。有向图也称为数字图或有向网络。下图表示一个有向图。这里,(A,B)、(B,C)、(C,E)、(E,D)、(E,F)和(D,B)边都是有向边。由于这些边都是有向边,因此边 AB 与边 BA 并不相同:
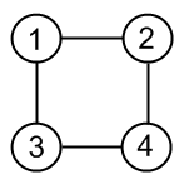
无向图
如果一个图只包含不定向边,那么这个图就是不定向图。换句话说,无向图中的边是双向的。有时,无向图也被称为无向网络。在无向图中,如果顶点 A 与顶点 B 相连,则假定 (A, B) 和 (B, A) 代表同一条边。下图显示了一个无向图的示例,其中所有的边都没有箭头表示方向:
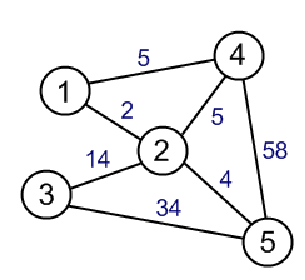
加权图
如果一个图的所有边都是加权边,那么这个图就称为加权图。我们将在接下来的章节中详细讨论加权图。加权图可以是有向图,也可以是无向图。每条边都必须有一个与之相关的值。边的权重通常称为边的代价。下图表示一个有五个顶点和七条边的无向加权图。其中,顶点 1 和 2 之间的边的权重为 2,顶点 1 和 4 之间的边的权重为 5,顶点 4 和 5 之间的边的权重为 58:
有向无环图 (DAG)
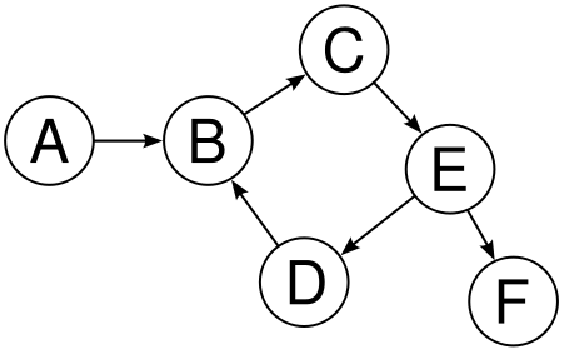
非循环图是指没有循环或环路的图。如果我们想从某个节点访问其他节点,我们不会重复访问任何节点。有向无环图,俗称 DAG,是一种无循环的有向图。有向无环图在图算法中有很多用途。有向无环图具有拓扑排序,即顶点的排序使得每条边的起点端点在排序中都早于终点端点。下图表示一个有向无环图:
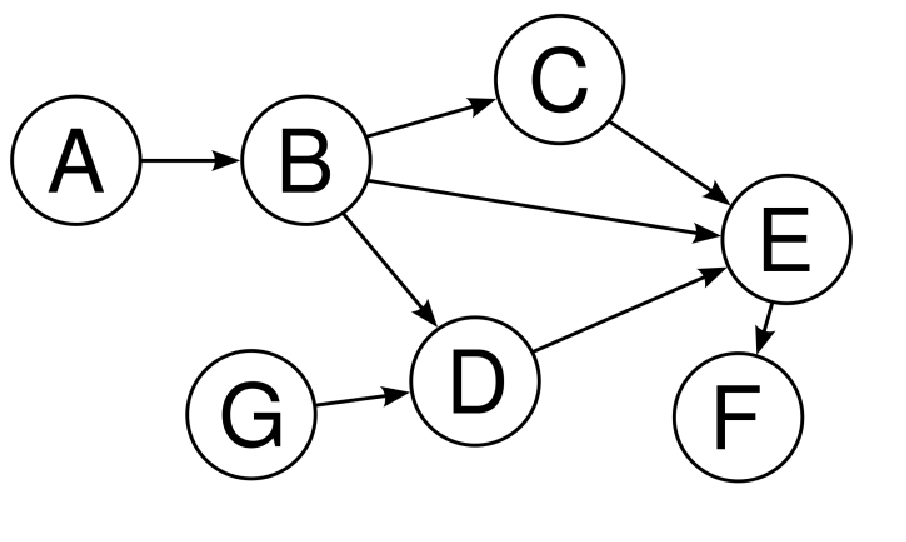
乍一看,B、C、E 和 D 似乎构成了一个循环,但仔细观察就会发现,它们并没有构成一个循环,而我们在有向图部分使用的示例就是一个完美的循环图示例。