使用 Dijkstra 算法的单源最短路径
我们可以使用 Floyd-Warshall 算法轻松找到最短路径,但却无法获得从节点 X 到 Y 的实际路径。这是因为 Floyd-Warshall 算法只计算距离或成本,并不存储最小成本的实际路径。例如,使用谷歌地图,我们总能找到从任何给定地点到达目的地的路线。谷歌地图可以为我们显示距离、旅行时间或其他因素方面的最佳路线。这就是使用单源最短路径算法的一个完美例子。有许多算法可以找到单源最短路径问题的解决方案,但是,Dijkstra 最短路径算法是最流行的算法。实现 Dijkstra 算法的方法有很多,如使用斐波那契堆、最小堆、优先队列等。每种实现方式在性能和改进 Dijkstra 算法方面都有自己的优势。让我们来看看该算法的伪代码:
function Dijkstra(Graph, source):
create vertex set Q
for each vertex v in Graph:
dist[v] := INFINITY
prev[v] := UNDEFINED
add v to Q
dist[source] := 0
while Q is not empty:
u := vertex in Q with min dist[u]
remove u from Q
for each neighbor v of u:
alt := dist[u] + length(u, v)
if alt < dist[v]:
dist[v] := alt
prev[v] := u
return dist[], prev[]现在,我们将使用优先级队列来实现该算法。首先,让我们选择一个图来实现算法。我们可以选择下面这个无向加权图。它有六个节点,节点和顶点之间有许多连接。首先,我们需要用邻接矩阵来表示下图:
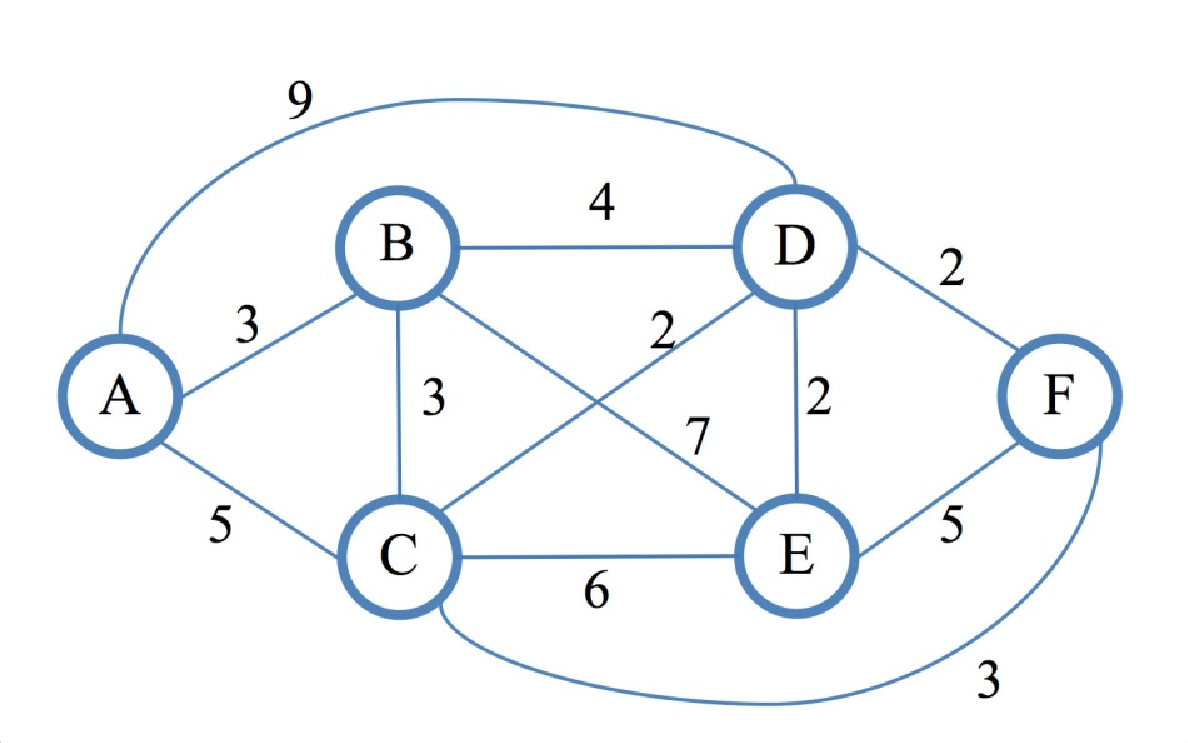
从上图可以看出,我们的顶点是用字母 A 至 F 标记的,因此我们将使用顶点名称作为 PHP 关联数组的键:
Unresolved include directive in modules/ROOT/pages/ch09/ch9-06.adoc - include::example$Chapter09/5.php[]现在,我们将使用优先级队列来实现 Dijkstra 算法。我们将使用上一个图中创建的邻接矩阵,找到一条从源顶点到目标顶点的路径。我们的 Dijkstra 算法将返回一个数组,其中包含两个节点之间的最小距离和所遵循的路径。我们将以堆栈的形式返回路径,这样就能以相反的顺序获得实际路径。下面是实现方法:
Unresolved include directive in modules/ROOT/pages/ch09/ch9-06.adoc - include::example$Chapter09/5.php[]从前面的实现中我们可以看到,首先,我们创建了两个数组来存储距离和前置数,以及优先级队列。然后,我们将每个顶点设置为 PHP 的最大整数(PHP_INT_MAX)值(伪代码中为 INFINITY),将前置节点设置为 NULL。我们还取了所有相邻节点的最小值并将其存储在队列中。循环结束后,我们将源节点距离设为 0。然后,我们检查队列中的每个节点,并检查最近的邻居,以找到一条最小路径。如果使用 if ($dist[$u] + $cost < $dist[$v]) 找到了路径,我们就将其分配给顶点。
然后,我们创建了一个名为 $s 的栈来存储路径。我们从目标顶点出发,访问相邻顶点,最终到达源顶点。当我们通过相邻顶点时,我们也计算了访问这些顶点所覆盖的距离。由于我们的函数同时返回距离和路径,因此我们构建了一个数组,以返回给定图形、源顶点和目标顶点的距离和路径。如果不存在路径,我们将返回 0 作为距离,并返回一个空栈作为输出。现在,我们将编写几行代码,使用图 $graph 和函数 Dijkstra 来检查我们的实现:
Unresolved include directive in modules/ROOT/pages/ch09/ch9-06.adoc - include::example$Chapter09/5.php[]如果运行这段代码,我们的命令行会有如下输出:
Distance from A to F is 8
Path to follow : A C F输出结果看起来完全正确,因为我们可以从图中看到,从 A 到 F 的最短路径是通过 C,最短的距离是 5 + 3 = 8。
Dijkstra 算法的运行复杂度为 \$O (V2)\$。由于我们使用的是最小优先级队列,因此运行复杂度为 \$O (E + V log V)\$。