使用 Floyd-Warshall 算法的最短路径

送披萨的公司经常要做的事情就是尽快送达披萨。在这种情况下，图算法可以帮助我们。Floyd-Warshall 算法是一种非常常见的算法，用于利用所有顶点对（u, v）找到从 u 到 v 的最短路径。最短路径表示相互连接的两个节点之间可能存在的最短距离。计算最短路径的图必须是加权图。在某些情况下，权重也可以是负数。该算法非常简单，是最容易实现的算法之一。如图所示：

for i:= 1 to n do
    for j:= 1 to n do
        dis[i][j] = w[i][j]

for k:= 1 to n do
    for i:= 1 to n do
        for j:= 1 to n do
            sum := dis[i][k] + dis[k][j]
            if (sum < dis[i][j])
                dis[i][j] := sum

首先，我们将每个权重复制到成本或距离矩阵中。如果距离或成本小于顶点 i 和顶点 j 之间的直接路径，我们就选择从 i 到 k 再到 j 的路径，而不是从 i 到 j 的直接路径。

请看下图：

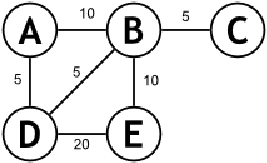
在这里，我们可以看到一个无向图，每条边都有权重。现在，如果我们寻找从 A 到 E 的最短路径，那么我们有以下选项：

A 经 B 到 E 的距离为 20
A 经 D 到 E 的距离为 25
A 经 D 和 B 到 E，距离为 20
A 经 B 和 D 到 E 的距离为 35

因此，我们可以看到最小的距离是 20。现在，让我们用顶点的数字表示来编程实现这一结果。我们将分别用 0、1、2、3 和 4 代替 A、B、C、D 和 E。现在，让我们用邻接矩阵的格式来表示前面的图形：

Unresolved include directive in modules/ROOT/pages/ch09/ch9-05.adoc - include::example$Chapter09/4.php[]

在这里，我们采取了一种不同的方法，将所有边初始化为 PHP 整数的最大值。这样做的原因是为了确保非边的值为 0 不会影响算法逻辑，因为我们正在搜索最小值。现在，我们需要将权重添加到图中，如上图所示：

Unresolved include directive in modules/ROOT/pages/ch09/ch9-05.adoc - include::example$Chapter09/4.php[]

由于这是一个无向图，我们给两条边分配了相同的值。如果这是一个有向图，我们可以只为每个权重设置一个条目。现在，是时候实现 Floyd-Warshall 算法，为任意给定的一对节点找出最短路径了。下面是我们对该函数的实现：

Unresolved include directive in modules/ROOT/pages/ch09/ch9-05.adoc - include::example$Chapter09/4.php[]

正如我们前面提到的，函数的实现非常简单。我们有三个内循环来计算最小距离，并在函数结束时返回距离数组。现在，让我们调用这个函数，检查一下我们的预期结果是否一致：

Unresolved include directive in modules/ROOT/pages/ch09/ch9-05.adoc - include::example$Chapter09/4.php[]

下面是代码的输出结果：

Shortest distance between A to E is:20
Shortest distance between D to C is:10

如果我们检查上一张图，我们可以看到 D 和 C 之间的最短距离实际上是 10，路径是 D → B → C (5+5)，这是所有可能路线中最短的距离 (D → A → B → C (20)，或 D → E → B → C (35))。

Floyd-Warshall 算法的复杂度为 \$O (V3)\$，其中 V 是图中的顶点数。现在我们将探索另一种因寻找单源最短路径而闻名的算法。