实现 Prim 的生成树算法

普里姆寻找最小生成树的算法依赖于一种贪婪的方法。贪心算法被定义为一种算法范式，在这种算法中，我们试图通过考虑每个阶段的局部最优解来找到全局最优解。我们将在第 11 章 "使用高级技术解决问题" 中探讨贪婪算法。在贪婪算法中，算法会创建边的子集，并从边的子集中找出成本最低的一条。这个边子集将包括所有顶点。它从一个任意位置开始，通过选择顶点之间最便宜的连接，每次增加一个顶点，从而形成一棵树。让我们来看看下面的图：

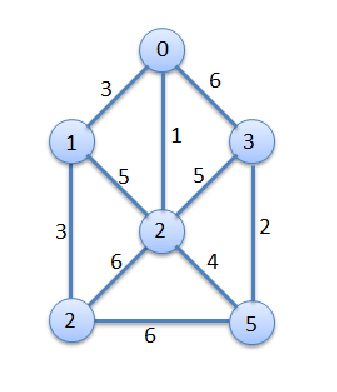
现在，我们将应用普里姆算法的一个非常基本的版本，来得到最小生成树以及边的最小成本或权重。图的邻接矩阵如下所示：

现在，我们将实现 Prim 最小生成树的算法。我们假设要从顶点 0 开始找出整棵生成树，因此只需在函数中传递图的邻接矩阵，它就会显示生成树的连接边和最小成本：

现在，如果我们使用图 $G 调用函数 primMST，算法的输出和构建的 MST 将如下所示：

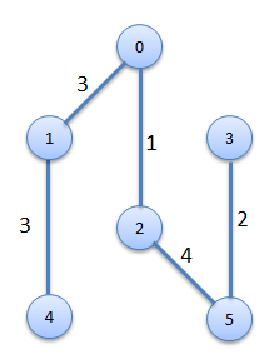
借助斐波那契堆、优先级队列等，还有其他方法来实现普里姆算法。该算法与 Dijkstra 寻找最短路径的算法十分相似。我们实现该算法的时间复杂度为 \$O (V2)\$。利用二进制堆和斐波那契堆，我们可以大大降低复杂度。