了解插入排序
到目前为止,我们已经了解了两种基于比较的排序算法。现在,我们将探讨另一种排序算法,与前两种算法相比,它具有一定的效率。我们现在讨论的是插入排序。与我们刚才看到的其他两种排序算法相比,它的实现最为简单。如果项目数较少,插入排序比冒泡排序和选择排序更有效。如果数据集较大,那么它就会像冒泡排序一样效率低下。由于插入排序的交换几乎是线性的,因此建议使用插入排序而不是冒泡排序和选择排序。
顾名思义,插入排序的工作原理是将数字插入左侧的正确位置。它从数组的第二个项目开始,检查左边的项目是否小于当前值。如果是,它就会移动项目,并将较小的项目存储到正确的位置。然后,它会移动到下一个项目,同样的原则一直持续到整个数组排序完毕。插入排序的伪代码是这样的:
procedure insertionSort( A : list of sortable items )
n = length(A)
for i = 1 to n inclusive do
key = A[i]
j = i - 1
while j >= 0 and A[j] > key do
A[j+1] = A[j]
j--
end while
A[j+1] = key
end for
end procedure如果我们考虑之前用于冒泡排序和选择排序的数字列表,那么就会出现以下情况,我们必须进行插入排序。我们数组中的元素是 20, 45, 93, 67, 10, 97, 52, 88, 33, 92.
让我们从第二个项目开始,即 45。现在,我们从 45 左边的第一项开始,到数组的开头,看看左边是否有大于 45 的值。由于只有 20,所以不需要插入,因为目前的项目已经排序到第二个元素(20,45)。现在,我们将指针移到 93,然后重新开始,从 45 开始比较数组左边的值,并搜索是否有更大的值。由于 45 不比 93 大,它就停止在这里,因为我们之前的结论是前两个项目已经排序。现在,我们对前三个项目(20、45、93)进行了排序。接下来是 67,我们再次从左边的数字开始比较。左边的第一个数字是 93,它的数字较大,因此必须移动一位。我们将 93 移到 67 的位置。然后,我们移动到它左边的下一个数字,即 45。45 比 67 小,不需要进一步比较。现在,我们将在 93 的位置上插入 67,93 必须移动到 67 的位置上。这样一直进行下去,直到整个数组排序完毕。
下图说明了在每个步骤中使用插入排序的完整排序过程:
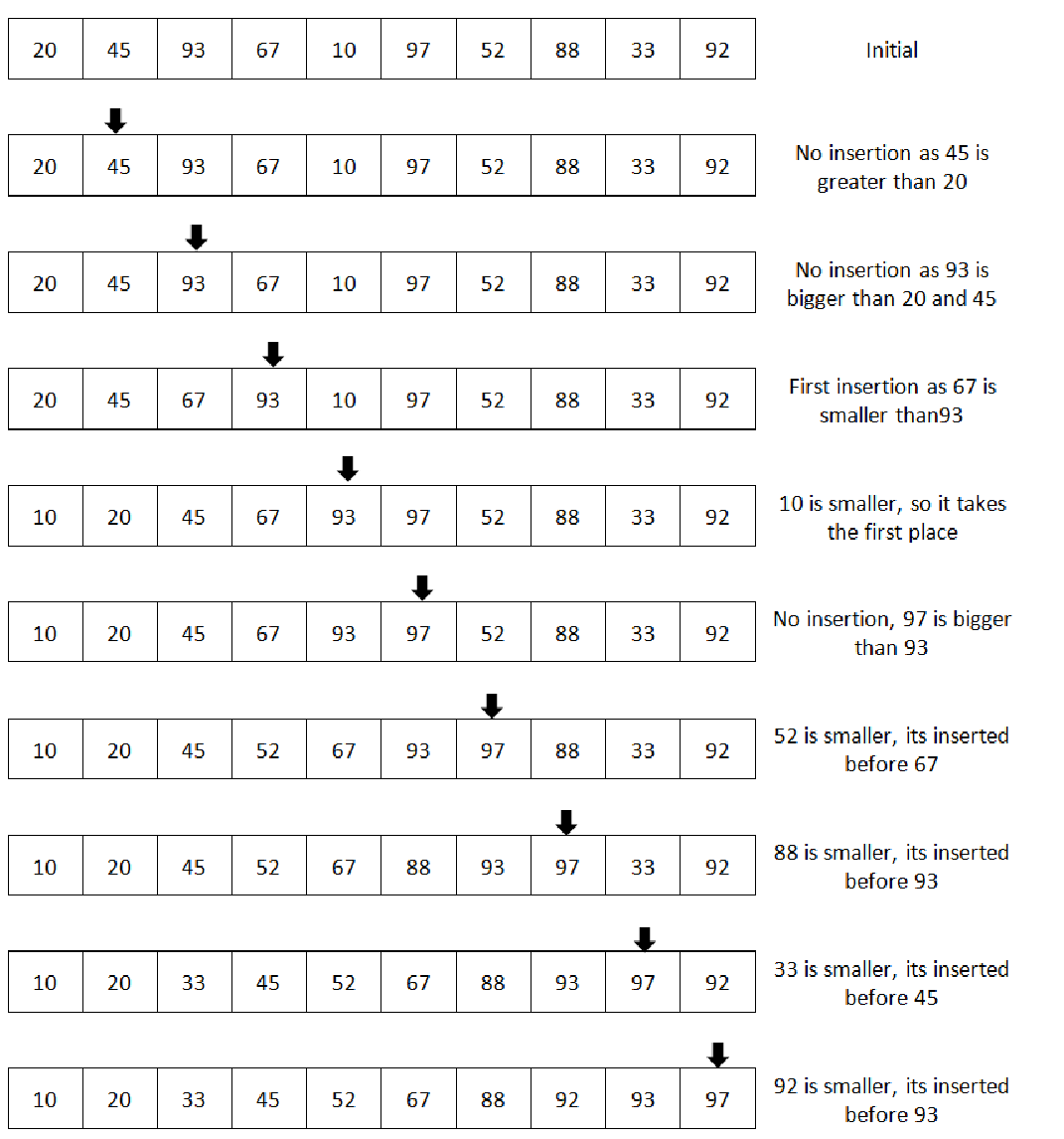
实现插入排序
我们将以与其他两种排序类似的方式实现插入排序,但有一个微妙的区别。这次,我们将以引用的形式传递数组。这样,我们就不需要函数的任何返回值了。如果需要,我们也可以通过值传递参数,并在函数结束时返回数组。下面是相关代码:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-04.adoc - include::example$Chapter07/6.php[]参数数组通过引用 (&$arr) 传递给函数。因此,将直接修改原始数组,而不是其副本。现在,我们要运行代码并检查输出结果。为此,我们必须运行以下代码:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-04.adoc - include::example$Chapter07/6.php[]|
如果我们以引用方式传递数组,则不必返回数组。传递的数组将在函数内部被修改。我们可以选择如何实现排序。 |