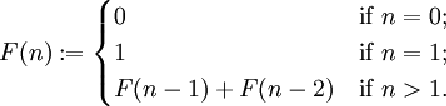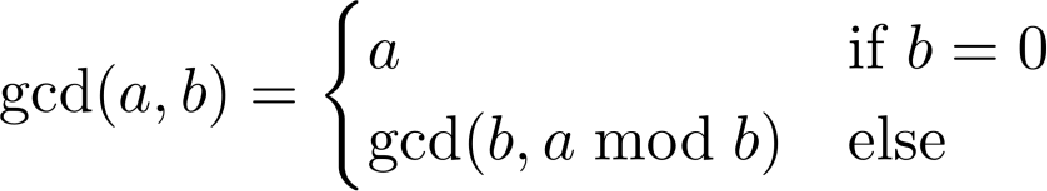理解递归
递归是一种将大问题分成小问题来解决的方法。换句话说,递归就是把大问题分解成更小的类似问题来解决,从而得到实际结果。递归通常被称为函数调用本身。这听起来可能很奇怪,但事实上,函数在递归时必须调用自身。这看起来像什么呢?我们来看一个例子。
在数学中,"阶乘" 一词非常流行。一个数字 N 的阶乘被定义为所有小于等于 N 的正整数的乘法!(感叹号)表示。因此,5 的阶乘可以这样写:
5! = 5 x 4 x 3 x 2 x 1同样,我们可以写出给定数字的以下阶乘:
4! = 4 x 3 x 2 x 1
3! = 3 x 2 x 1
2! = 2 x 1
1! = 1如果仔细观察我们的例子,就会发现我们可以这样用 4 的阶乘来写 5 的阶乘:
5! = 5 x 4!同样,我们可以写道:
4! = 4 x 3!
3! = 3 x 2!
2! = 2 x 1!
1! = 1 x 0!
0! = 1或者,我们可以笼统地简单地说:
n! = n * (n-1)!这就是递归。我们将每个步骤分解成更小的步骤,然后解决实际的大问题。下面的图片展示了如何计算 3 的阶乘:

因此,步骤如下:
-
3! = 3 x 2!
-
2! = 2 x 1!
-
1! = 1 x 0!
-
0! = 1
-
1! = 1 x 1 = 1
-
2! = 2 x 1 = 2
-
3! = 3 x 2 = 6
递归算法的性质
现在,问题可能是:"如果函数调用自身,那么它如何停止或知道何时完成递归调用?" 在编写递归解决方案时,我们必须确保它具有以下属性:
-
每次递归调用都应针对一个较小的子问题。就像阶乘的例子一样,6 的阶乘用 6 和 5 的阶乘相乘来解决,如此类推。
-
必须有基数。当达到基例时,就不会再有进一步的递归,基例必须能够解决问题,而不需要任何进一步的递归调用。在我们的阶乘例子中,我们没有从 0 开始继续往下,所以在这种情况下,0 就是我们的基例。
-
不应该有任何循环。如果每次递归调用都调用同一个问题,那么就会出现永无止境的循环。重复几次后,计算机就会出现堆栈溢出错误。
因此,如果我们现在使用 PHP 7 编写阶乘程序,那么它将如下所示:
function factorial(int $n): int {
if ($n == 0)
return 1;
return $n * factorial($n - 1);
}在前面的示例代码中,我们可以看到一个基本条件,即当 $n 的值为 0 时,我们将返回 1;如果不满足这个条件,我们将返回 $n 的乘法和 $n-1 的阶乘。因此,它满足 1 和 3 这两个数字的属性。我们正在避免循环,并确保每次递归调用都是在创建大问题的子问题。我们将按照下面的算法来编写递归行为:
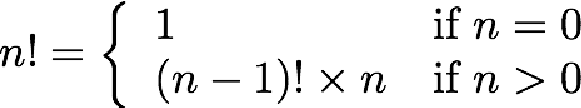
递归与迭代算法
如果我们分析一下阶乘函数,就会发现它可以用 for 或 while 循环的简单迭代法来编写,如图所示:
Unresolved include directive in modules/ROOT/pages/ch05/ch5-01.adoc - include::example$Chapter05/1.php[]如果这可以写成一个简单的迭代,那么我们为什么要使用递归呢?递归用于解决更复杂的问题。并不是所有问题都能这么容易地用递归法解决。例如,我们需要显示某个目录下的所有文件。我们可以简单地通过运行一个循环来列出所有文件。但是,如果目录内还有另一个目录呢?那么,我们就必须运行另一个循环来获取该目录中的所有文件。如果该目录内又有另一个目录,并且一直循环下去呢?在这种情况下,迭代方法可能根本无济于事,或者会产生一个复杂的解决方案。在这种情况下,最好选择递归方法。
递归管理一个调用堆栈,用于管理函数调用。因此,与迭代相比,递归需要更多内存和时间才能完成。此外,在迭代中,每一步都能得到结果,但在递归中,我们必须等到基例执行完毕才能得到任何结果。如果我们同时考虑阶乘的迭代和递归示例,我们可以看到有一个名为 $result 的局部变量用于存储每一步的计算结果。然而,在递归中,不需要本地变量或赋值。