0 - 1 背包

背包是一种有带子的袋子，通常由士兵携带，帮助他们在旅途中携带必要的物品或贵重物品。每件物品都有一定的价值和重量。因此，士兵必须在最大重量限制内挑选最贵重的物品，因为他们不可能把所有东西都放进包里。0/1 这个词的意思是，我们要么拿走它，要么把它留下。我们不能拿走部分物品。这就是著名的 0-1 包问题。我们将采用自下而上的方法来解决 0-1 包问题。下面是解题的伪代码：

Procedure knapsack(n, W, w1,...,wN, v1,...,vN)
    for w = 0 to W
        M[0, w] = 0

    for i = 1 to n
        for w = 0 to W
            if wi > w :
                M[i, w] = M[i-1, w]
            else :
                M[i, w] = max (M[i-1, w], vi + M[i-1, w-wi ])
    return M[n, W]

end procedure

例如，如果我们有五个项目 [1,2,3,4,5]，它们的权重分别为 10、20、30、40、50，那么最大允许权重为 10 的自下而上法将产生下表：

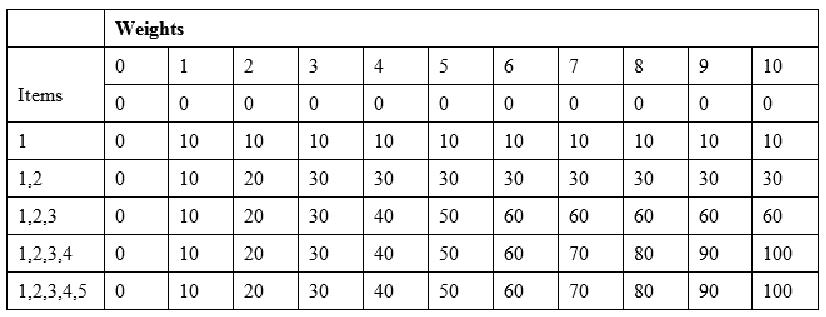
image 2023 11 09 09 18 05 283

正如我们所看到的，我们自下而上地建立表格，从一个项目和一个权重开始，然后增加到我们想要的权重，并通过选择尽可能好的项目来最大化值数。最后，右下角的最后一个单元格就是 0-1 包问题的预期结果。下面是函数的实现和运行代码：

Unresolved include directive in modules/ROOT/pages/ch11/ch11-07.adoc - include::example$Chapter11/6.php[]