回溯解决难题

回溯是一种递归算法策略，当没有找到结果时，我们会回溯，并继续用其他可能的方法寻找解决方案。回溯是解决许多著名问题的常用方法，尤其是国际象棋、数独、填字游戏等。由于递归是反向追踪的关键组成部分，我们需要确保我们的问题可以划分为若干子问题，并在这些子问题中应用递归。在本节中，我们将使用反向追踪来解决最流行的游戏之一—​数独。

在数独游戏中，我们有一个部分填满的盒子，里面有大小为 3X3 的漂亮盒子。游戏规则是在每个单元格中填入 1 到 9 的数字，同一数字不能出现在同一行或同一列中。因此，在 9X9 单元格中，每个数字 1 到 9 在每一行和每一列中只能出现一次：

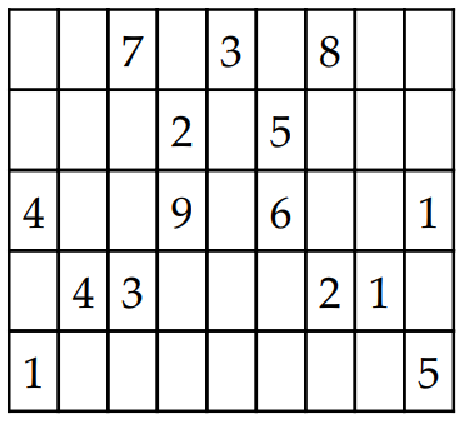
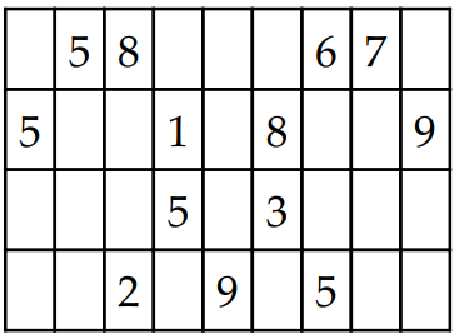
例如，在前面的数独棋盘中，第一列有 4、1、5，第一行有 7、3、8。因此，我们不能在左上角的第一个空格中使用这六个数字中的任何一个。因此，可能的数字是 2、6 和 9。我们不知道哪一个数字能满足解题要求。我们可以选择两个数字填入第一个单元格，然后开始为其余的空单元格寻找数值。这样一直进行下去，直到所有的单元格都被填满，或者仍然有办法在不违反博弈原则的情况下在空单元格中填入一个数字。如果无解，我们就会回到 2，用下一个可能的选项 6 取而代之，然后用同样的递归方法为其他空格寻找数字。这个过程一直持续到棋盘解出为止。让我们编写一些递归代码来解数独：

在这里，我们可以看到实现数独函数所需的所有辅助函数。首先，我们定义了网格的最大尺寸和未分配单元格指示符，在本例中指示符为 0。我们的第一个函数是在 9 X 9 的网格中找到任何未分配的位置，从左上角的单元格开始，按行搜索空单元格。然后，我们有三个函数来检查某个数字是否在特定行、列或 3 X 3 方格中使用。如果该行、列或方框中没有使用该数字，我们可以将其作为单元格中的一个可能值，这就是我们在 isSafe 函数检查中返回 true 的原因。如果在上述任何一处使用，函数将返回 false。现在，我们准备好实现用于解数独的递归函数了：

SolveSudoku 函数的功能不言自明。在这里，我们访问一个单元格，如果该单元格为空，则在该单元格中放入一个临时数字，从 1 到 9 的任意数字。然后，我们检查该数字在行中、列中或 3 X 3 矩阵中是否多余。如果不冲突，我们就将数字保留在单元格中，然后移动到下一个空单元格。我们通过递归的方式来完成这项工作，这样如果有需要，我们就可以在出现冲突时回溯并更改数值。这个过程一直持续到找到解决方案为止。我们还添加了一个 printGrid 函数，用于在命令行中打印给定的网格。现在，让我们用本示例中使用的数独矩阵示例运行代码：

我们使用二维数组来表示数独矩阵。如果我们运行代码，它将在命令行中产生以下输出：

或者，如果我们将其呈现在一个漂亮的数独矩阵中，它将如下所示：

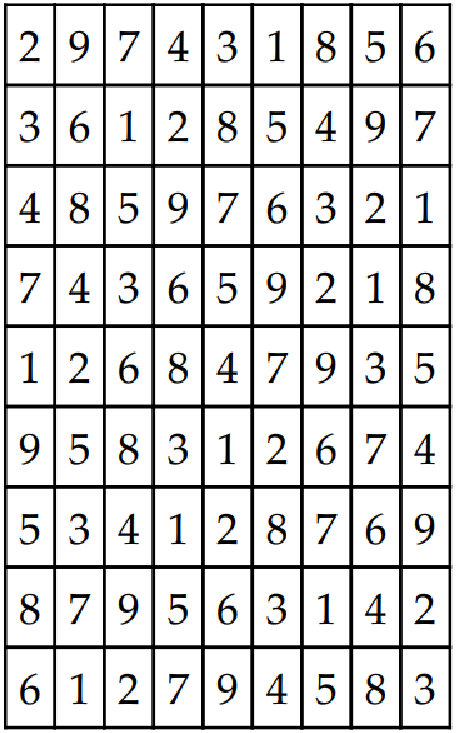
回溯法对于寻找路径或解决游戏问题非常有用。网上有很多关于回溯的参考资料，对我们非常有用。