了解图属性
图是通过边相互连接的顶点或节点的集合。这些边可以是有序的,也可以是无序的,这意味着边可以是有方向的,也可以是无方向的,这也被称为双向边。我们用顶点 V 和边 E 组成的集合 G 来表示图,如下所示:
G = (V, E)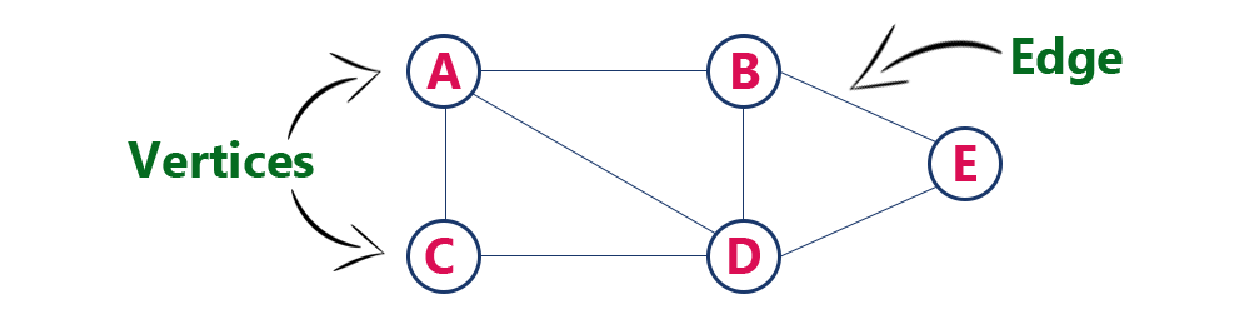
在上图中,我们有五个顶点和六个边:
V = {A, B, C, D, E}
E = {AB, AC, AD, BD, BE, CD, DE}如果我们看前面的图,A 和 B 之间的连通性可以表示为 AB 或 BA,因为我们还没有定义连通性的方向。图数据结构与树数据结构的一个显著区别是,图数据结构可以形成循环或环路,而树数据结构则不能。与树形数据结构不同,我们可以从图形数据结构中的任意顶点开始。此外,我们可以在任意两个顶点之间建立直接边,而在树形数据结构中,只有当子节点是父节点的直系后代时,两个节点才能相连。
与图有关的属性和关键词多种多样。在进一步讨论图及其应用之前,我们将探讨这些术语。
边缘
边是两个顶点之间的连接。通常,它由两个顶点之间的一条线表示。在上一幅图中,A 和 B、A 和 C、A 和 D、B 和 D、C 和 D、B 和 E 以及 D 和 E 之间都有边。边有三种类型:
-
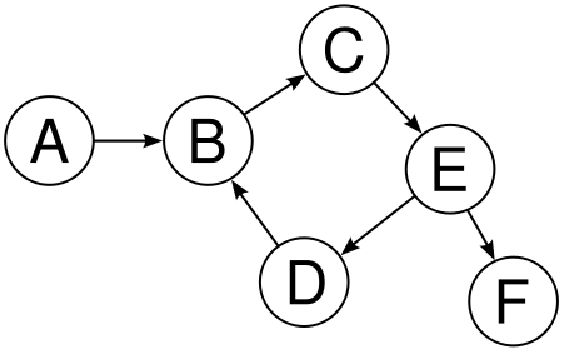
定向边:如果一条边上标有箭头,则表示它是一条有向边。有向边是单向的。箭头的头部是结束顶点,箭头的尾部是开始顶点:
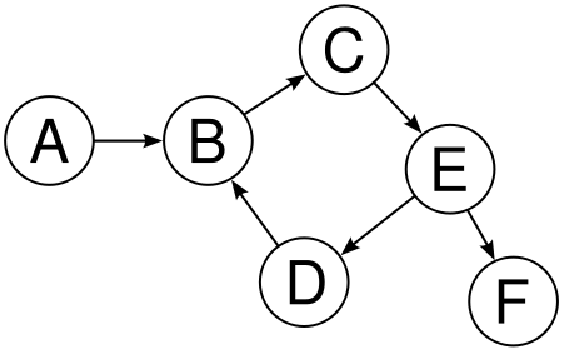
在上图中,我们可以看到 A 有一条指向 B 的有向边,这意味着 A、B 是一条边,反之则不是(B、A)。因此,这是一个单向边或有向边的例子。
-
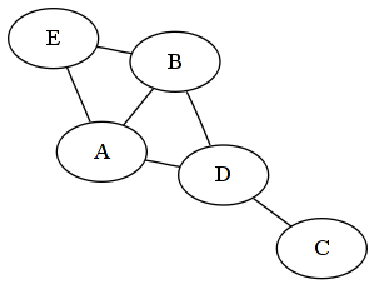
无向边:无向边是两个顶点之间没有任何方向的连接。这意味着该边满足双向关系。下图是一个无向图的示例,其中 A 与 B 的连接方式使得两条边 (A, B) 和 (B, A) 相同:
-
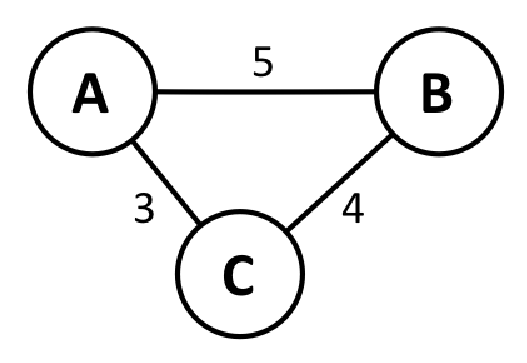
加权边:当一条边携带附加信息(例如成本、距离或其他信息)时,我们将该边称为加权边。 这用于许多图算法。 在下图中,边 (A, B) 的权重为 5。根据图的定义,这可以是距离、成本或任何内容:
邻近的
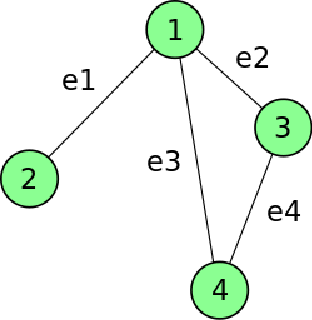
如果两个顶点之间有一条边,它们就是相邻的。如果两个顶点 A 和 B 之间有一条直接边,那么这两个顶点就是相邻的。在下图中,我们可以看到顶点 1 和顶点 2 通过边 e1 相连,因此它们被称为相邻。由于顶点 2 在顶点 3 和顶点 4 之间没有边,因此顶点 2 与顶点 3 和顶点 4 不相邻。
事件
如果一条边的顶点是该边的端点之一,那么这条边就是该顶点的入射边。此外,如果两条边共享一个顶点,那么这两条边也是入射的。如果我们看下图,我们可以看到入射边 (e1,e2)、(e2,e3) 和 (e1,e3) 共享顶点 1。此外,还有共用顶点 4 的入射边 (e3,e4) 和共用顶点 3 的入射边 (e2,e4)。同样,我们可以说顶点 1 在边 e1、e2 和 e3 上有附点,顶点 2 在边 e1 上有附点,顶点 3 在边 e2 和 e4 上有附点,顶点 4 在边 e3 和 e4 上有附点: