重新审视图的 BFS 和 DFS

我们现在要实现一个图的 BFS。首先，我们需要用矩阵或列表来表示下面的无向图。为简单起见，我们将使用邻接矩阵来表示图：

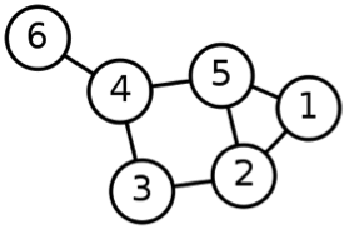
前面的邻接图有六个顶点，顶点的标号从 1 到 6（没有 0）。由于顶点是有编号的，因此我们可以使用这些顶点作为数组索引，以加快访问速度。我们可以这样构建图：

在这里，我们有两个数组，一个用于表示实际图形，另一个用于记录访问过的节点。我们要确保不会多次访问一个节点，因为这可能会导致无限循环。由于我们的图形有 6 个顶点，因此我们将 $vertexCount 保持为 6。 然后，我们将图形数组初始化为初始值为 0 的二维数组。我们还将 $visited 数组中的每个顶点赋值为 0，从而将每个顶点设置为未访问。现在，我们将在图中添加边。由于图是不定向的，我们需要为每条边设置两个属性。换句话说，我们需要为标有 1 和 2 的顶点之间的边设置双向边值，因为这两个顶点之间共享一条边。以下是完整表示先前图形的代码：

因此，我们使用邻接矩阵来表示图。现在，我们来定义矩阵的 BFS 算法：

我们实现的 BFS 函数需要三个参数：实际图形、起始顶点和空访问数组。我们本可以避免第三个参数，而将初始化写入 BFS 函数内部。最后，我们可以选择其中任何一种方法来实现这一目标。在我们的函数实现中，我们有两个队列：一个用于保存需要访问的节点，另一个用于保存已访问节点的顺序或搜索路径。函数结束时，我们将返回路径队列。

在函数内部，我们首先将起始节点添加到队列中。然后，我们从该节点开始访问其相邻节点。如果该节点未被访问，且与当前节点有连接，我们就将其添加到队列中进行访问。我们还会将当前节点标记为已访问节点，并将其添加到我们的路径中。现在，我们将使用构建的图矩阵和访问节点调用 BFS 函数。下面是执行 BFS 功能的程序：

从前面的代码片段可以看出，我们从节点 1 开始搜索。输出结果如下：

如果我们将 BFS 函数调用的第二个参数从 1 改为 5，将 5 作为起始节点，那么输出结果就会如下：

正如我们在 BFS 中看到的那样，我们也可以为 DFS 定义任何起始顶点。不同之处在于，对于访问节点列表，我们将使用堆栈而不是队列。代码的其他部分与 BFS 代码类似。我们还将使用与 BFS 实现相同的图。我们要实现的 DFS 是迭代式的。下面是它的代码：

如前所述，对于 DFS，我们必须使用堆栈而不是队列，因为我们需要堆栈中的最后一个顶点，而不是第一个顶点（如果我们使用队列的话）。对于路径部分，我们使用队列，以便在显示过程中按顺序显示路径。下面是调用图形 $graph 的代码：

代码的输出结果如下：

在前面的例子中，我们从顶点 1 开始，在顶点 1 标签为 5 和 2 的两个相邻顶点中，我们将首先访问顶点 5。现在，顶点 5 有两个标签为 4 和 2 的顶点。顶点 4 将首先被访问，因为它是顶点 5 的第一条边（请注意我们从左到右的节点访问方向）。接下来，我们将从顶点 4 开始访问顶点 6。由于我们无法从顶点 6 继续前进，因此它将返回顶点 4，并访问未访问的相邻顶点，标签为 3。当我们位于顶点 3 时，从 3 开始有两个相邻顶点，它们分别被标记为顶点 4 和顶点 2。我们之前已经访问过顶点 4，因此不能再访问它，只能从顶点 3 访问顶点 2。由于顶点 2 有三个顶点，分别是顶点 3、5 和 1，而且它们都已被访问过，因此我们实际上已经完成了 DFS 实现。