使用卡恩算法的拓扑排序

假设我们有一些任务要做，而每个任务都有一些依赖关系，这意味着在做实际任务之前，应先完成依赖任务。当任务和依赖关系之间存在相互关系时，问题就出现了。现在，我们需要为完成任务制定一个适当的顺序。我们需要一种特殊的排序方式，以便在不违反完成任务规则的情况下对这些相互关联的任务进行排序。拓扑排序是解决此类问题的正确选择。在拓扑排序中，从顶点 A 到 B 的有向边 AB 的排序方式是，在排序中 A 总是排在 B 之前。这适用于所有顶点和边。应用拓扑排序的另一个重要因素是图必须是 DAG。任何 DAG 都至少有一种拓扑排序。大多数情况下，一个给定的图可能有多种拓扑排序。目前有两种流行的拓扑排序算法：卡恩算法和 DFS 方法。我们将在此讨论 Kahn 算法，因为我们已经在本书中多次讨论过 DFS。

Kahn 算法有以下步骤来从 DAG 中找到拓扑排序：

计算每个顶点的indegree（传入边），并将所有顶点放入 indegree 为 0 的队列中，同时将已访问节点的计数初始化为 0。
从队列中移除一个顶点，并对其执行以下操作：
- 将已访问节点数增加 1。
- 将所有相邻顶点的 indegree 减少 1。
- 如果相邻顶点的 indegree 为 0，则将其添加到队列中。
重复步骤 2，直到队列为空。
如果被访问节点的计数与节点的计数不相同，则给定的 DAG 无法进行拓扑排序。

让我们来看看下面的图。这是一个完美的 DAG 例子。现在，我们想使用拓扑排序和卡恩算法对它进行排序：

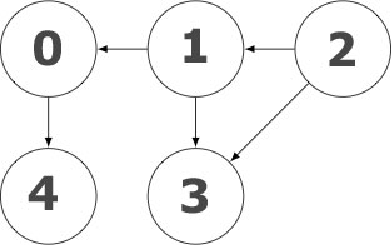
现在，让我们用邻接矩阵来表示这个图，就像之前对其他图所做的那样。矩阵如下：

$graph = [
    [0, 0, 0, 0, 1],
    [1, 0, 0, 1, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0],
];

现在，我们将按照规定的步骤实现卡恩算法。下面是其实现过程：

Unresolved include directive in modules/ROOT/pages/ch09/ch9-04.adoc - include::example$Chapter09/1.php[]

从前面的实现中我们可以看到，我们实际上已经考虑到了卡恩算法的每一个步骤。首先，我们找到了顶点的 indegree，并将 indegree 为 0 的顶点放入一个队列中。然后，我们检查队列中的每个节点，减少相邻顶点的指数，并再次将指数为 0 的相邻顶点加入队列。最后，我们返回排序后的队列，如果有序顶点数与实际顶点数不符，则返回空队列。现在我们可以调用函数，将已排序的顶点列表作为队列返回。代码如下：

Unresolved include directive in modules/ROOT/pages/ch09/ch9-04.adoc - include::example$Chapter09/1.php[]

现在，将逐一查看队列元素并打印出来。输出结果如下：

2 1 0 3 4

输出结果符合我们的预期。从前面的图中我们可以看到，顶点 2 与顶点 1 和顶点 3 有一条直接边，而顶点 1 与顶点 0 和顶点 3 有一条直接边。由于顶点 2 没有进入的边，我们将从顶点 2 开始进行拓扑排序。顶点 1 有一条进入边，顶点 3 有两条进入边，因此，在顶点 2 之后，我们将按照算法访问顶点 1。按照同样的原则，我们将访问顶点 0，然后是顶点 3，最后是顶点 4。我们还必须记住，一个给定的图可能有多种拓扑排序。卡恩算法的复杂度为 \$O (V+E)\$，其中 V 是顶点数，E 是边数。