寻找最长公共子序列-LCS

另一种非常流行的动态编程算法是寻找两个字符串之间的最长公共子序列（或 LCS）。这个过程与 "knapsack" 解法非常相似，在 "knapsack" 解法中，我们有一个二维表，从一个权重开始，移动到目标权重。在这里，我们将从第一个字符串的第一个字符开始，在整个字符串中移动以匹配第二个字符串的字符。我们将继续这样做，直到第一个字符串的所有字符都与第二个字符串的单个字符匹配。因此，当我们找到匹配时，我们会考虑匹配单元格的左上角单元格或对角线左侧单元格。让我们看看下面两张表格，以了解匹配是如何发生的：

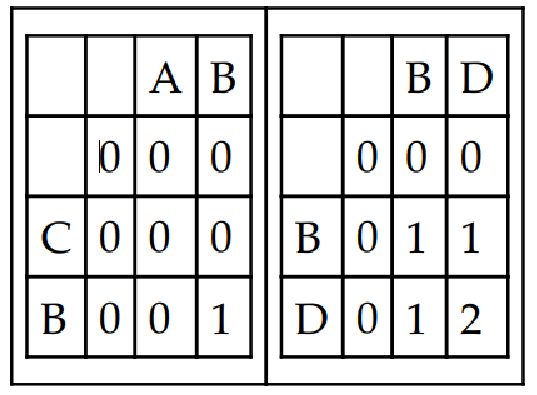
image 2023 11 09 09 22 34 197

在左边的表格中，我们有两个字符串 AB 和 CB。当 B 与表格中的 B 相匹配时，匹配单元格的值将是其对角线单元格的值加 1。这就是为什么第一个表格的深色背景单元格的值为 1，因为对角线左侧单元格的值为 0。出于同样的原因，右边表格的右侧最低单元格的值为 2，因为对角线单元格的值为 1。以下是查找 LCS 长度的伪代码：

function LCSLength(X[1..m], Y[1..n])
    C = array[m][n]
    for i := 0..m
        C[i,0] = 0
    for j := 0..n
        C[0,j] = 0
    for i := 1..m
        for j := 1..n
            if(i = 0 or j = 0)
                C[i,j] := 0
            else if X[i] = Y[j]
                C[i,j] := C[i-1,j-1] + 1
            else
                C[i,j] := max(C[i,j-1], C[i-1,j])
    return C[m,n]

以下是查找 LCS 长度的伪代码的实现：

Unresolved include directive in modules/ROOT/pages/ch11/ch11-08.adoc - include::example$Chapter11/7.php[]

现在，让我们用两个字符串运行 LCS 函数，看看能否找到最长公共子序列：

Unresolved include directive in modules/ROOT/pages/ch11/ch11-08.adoc - include::example$Chapter11/7.php[]

这将在命令行中输出 LCS Length:5。这似乎是正确的，因为两个字符串的共同子序列都是 GGTAB。