树搜索
搜索分层数据的最佳方法之一是创建搜索树。在第 6 章 "理解并实现树" 中,我们了解了如何构建二叉搜索树并提高搜索效率。我们还发现了遍历树的不同方法。现在,我们将探讨搜索树结构最常用的两种方法,即广度优先搜索 (BFS) 和深度优先搜索 (DFS)。
广度优先搜索
在树形结构中,根节点与其子节点相连,每个子节点都可以表示为一棵树。我们在第 6 章 "理解和实现树" 中已经看到了这一点。在广度优先搜索(俗称 BFS)中,我们从一个节点(多为根节点)开始,首先访问所有相邻节点或邻居节点,然后再访问其他邻居节点。换句话说,在应用 BFS 时,我们必须逐级移动。由于我们是逐级搜索,因此这种技术被称为广度优先搜索。在下面的树形结构中,我们可以使用 BFS:
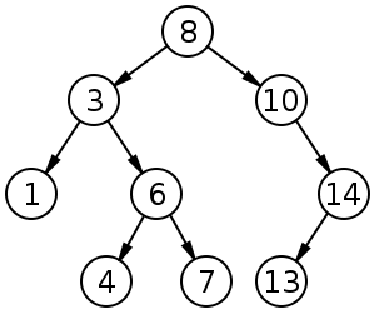
对于这棵树,BFS 将遵循这样的节点:8→3→10→1→6→14→4→7→13
BFS 的伪代码如下所示:
procedure BFS(Node root)
Q := empty queue
Q.enqueue(root);
while(Q != empty)
u := Q.dequeue()
for each node w that is childnode of u
Q.enqueue(w)
end for each
end while
end procedure我们可以看到,我们保留了一个队列,用于跟踪需要访问的节点。我们可以保留另一个队列来保存访问序列,并返回它以显示访问序列。现在,我们将使用 PHP 7 实现 BFS。
实现广度优先搜索
由于到目前为止我们还没有详细介绍图形,因此我们将严格按照树结构来实现 BFS 和 DFS。此外,我们将使用在第 6 章 "理解和实现树" 中看到的通用树结构(甚至不是二叉树)。我们将使用相同的 TreeNode 类来定义节点和与子节点的关系。现在,让我们定义具有 BFS 功能的树类:
Unresolved include directive in modules/ROOT/pages/ch08/ch8-06.adoc - include::example$Chapter08/8.php[]我们在树类中实现了 BFS 方法。我们将根节点作为广度优先搜索的起点。在这里,我们有两个队列:一个用于保存我们需要访问的节点,另一个用于保存我们已经访问过的节点。我们还将在方法结束时返回已访问队列。现在让我们模仿本节开始时看到的树。我们要把数据放到如图所示的树中,同时检查 BFS 是否真的返回了我们预期的模式;8→3→10→1→6→14→4→7→13:
Unresolved include directive in modules/ROOT/pages/ch08/ch8-06.adoc - include::example$Chapter08/8.php[]在这里,我们通过创建节点并将它们连接到根节点和其他节点来构建整个树形结构。树建好后,我们将调用 BFS 方法来查找完整的遍历序列。最后的 while 循环将打印我们访问过的节点序列。下面是前面代码的输出结果:
8
3
10
1
6
14
4
7
13我们得到了预期结果。现在,如果我们想搜索某个节点是否存在,可以为 $current 节点值添加一个简单的条件检查。如果匹配,我们就可以返回访问过的队列。
BFS 的最坏复杂度为 \$O (|V| + |E|)\$,其中 V 是顶点或节点的数量,E 是节点之间的边或连接的数量。就空间复杂度而言,最坏情况为 \$O (|V|)\$。
图 BFS 与此类似,但略有不同。由于图可能是循环的(可以形成循环),我们需要确保不会重复访问同一个节点,从而形成无限循环。为了避免重复访问图节点,我们必须跟踪已访问过的节点。为了标记已访问的节点,我们可以使用队列或图形着色算法。我们将在下一章对此进行探讨。
深度优先搜索
深度优先搜索(Depth first search,简称 DFS)是一种搜索技术,我们从一个节点开始搜索,从目标节点通过分支尽可能深入到节点。DFS 与 BFS 不同,我们会尽量深入挖掘,而不是先分散开。DFS 会垂直生长,到达分支末端时会回溯,并移动下一个可用的相邻节点,直到搜索结束。我们可以将上一节中的树形图复制如下:
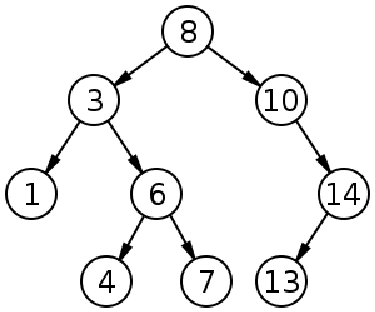
如果我们在这里应用 DFS,遍历结果将是 8→3→1→6→4→7→10→14→13。我们从根节点开始,然后访问第一个子节点,也就是 3。不过,我们不会像 BFS 那样访问到 10,而是会探索 3 的子节点,如此反复进行,直到到达分支的底部。在 BFS 中,我们采用了迭代法。对于 DFS,我们将采用递归方法。现在让我们编写 DFS 的伪代码:
procedure DFS(Node current)
for each node v that is childnode of current
DFS(v)
end for each
end procedure实施深度优先搜索
DFS 的伪代码看起来很简单。为了跟踪节点的访问顺序,我们需要使用一个队列,它将跟踪树类中的节点。下面是我们使用递归 DFS 实现的 Tree 类:
Unresolved include directive in modules/ROOT/pages/ch08/ch8-06.adoc - include::example$Chapter08/9.php[]我们可以看到,我们在树类中添加了一个额外的属性 $visited 来跟踪已访问的节点。在调用 DFS 方法时,我们将节点添加到队列中。现在,如果我们使用上一节中的相同树结构,并添加 DFS 调用并获取已访问的部分,它将看起来像这样:
Unresolved include directive in modules/ROOT/pages/ch08/ch8-06.adoc - include::example$Chapter08/9.php[]由于 DFS 不会返回任何内容,因此我们使用类属性 visited 来获取队列,以便显示已访问节点的序列。如果我们在控制台中运行这个程序,会有如下输出:
8
3
1
6
4
7
10
14
13结果与预期相符。如果我们需要 DFS 的迭代解决方案,我们必须记住,我们需要使用堆栈而不是队列来跟踪下一个要访问的节点。然而,由于栈遵循后进先出原则,对于我们提到的图象,输出结果将与我们最初的想法不同。下面是使用迭代方法的实现过程:
Unresolved include directive in modules/ROOT/pages/ch08/ch8-06.adoc - include::example$Chapter08/10.php[]它看起来与我们的迭代 BFS 算法非常相似。主要区别在于使用堆栈数据结构而不是队列数据结构来存储访问的节点。这也会对输出产生影响。前面的代码会产生 8 → 10 → 14 → 13 → 3 → 6 → 7 → 4 → 1 的输出。这与上一节的输出结果不同。由于我们使用了栈,因此输出结果实际上是正确的。我们使用堆栈来推送特定节点的子节点。对于值为 8 的根节点,第一个子节点的值为 3,它被推入堆栈,然后,根节点的第二个子节点的值为 10,也被推入堆栈。由于值 10 是最后推送的,因此它将遵循堆栈的后进先出原则排在前面。因此,如果我们使用堆栈,排序总是从最后一个分支开始到第一个分支。但是,如果我们想保持从左到右的节点排序,那么就需要对 DFS 代码稍作调整。下面是做了修改的代码块:
Unresolved include directive in modules/ROOT/pages/ch08/ch8-06.adoc - include::example$Chapter08/10.php[]与之前代码块的唯一区别是,我们在访问某个节点的子节点之前添加了下面一行:
$current->children = array_reverse($current->children);由于堆栈采用的是后进先出(LIFO)方式,因此通过逆转,我们可以确保第一个节点先被访问,因为我们逆转了顺序。事实上,它只是作为一个队列运行。这将产生所需的序列,如 DFS 部分所示。如果我们有一棵二叉树,那么不需要颠倒顺序也能轻松完成,因为我们可以选择先推右边的子节点,然后再推左边的子节点,这样就能先弹出左边的子节点。
DFS 的最坏复杂度为 \$O (|V| + |E|)\$,其中 V 是顶点或节点数,E 是节点间的边或连接数。就空间复杂度而言,最坏情况为 \$O (|V|)\$,与 BFS 相似。