了解冒泡排序
气泡排序是编程世界中最常用的排序算法。大多数程序员都是从这种算法开始学习排序的。它是一种基于比较的排序算法,一直被称为最低效的排序算法之一。它需要的比较次数最多,平均复杂度和最坏情况下的复杂度相同。
在冒泡排序中,列表中的每个条目都要与其他条目进行比较,并在需要时进行交换。列表中的每个条目都要这样做。我们可以按升序或降序排序。下面是冒泡排序的伪算法:
procedure bubbleSort( A : list of sortable items )
n = length(A)
for i = 0 to n inclusive do
for j = 0 to n-1 inclusive do
if A[j] > A[j+1] then
swap( A[j], A[j+1] )
end if
end for
end for
end procedure从前面的伪代码中可以看出,我们正在运行一个循环,以确保遍历列表中的每个项目。内循环确保一旦我们指向一个项目,就会将该项目与列表中的其他项目进行比较。根据我们的偏好,我们可以交换两个项目。下图显示了对列表中一个项目进行排序的单次迭代。假设我们的列表中有以下项目: 20, 45, 93, 67, 10, 97, 52, 88, 33, 92. 在对第一个条目进行第一次排序(迭代)时,将采取以下步骤:
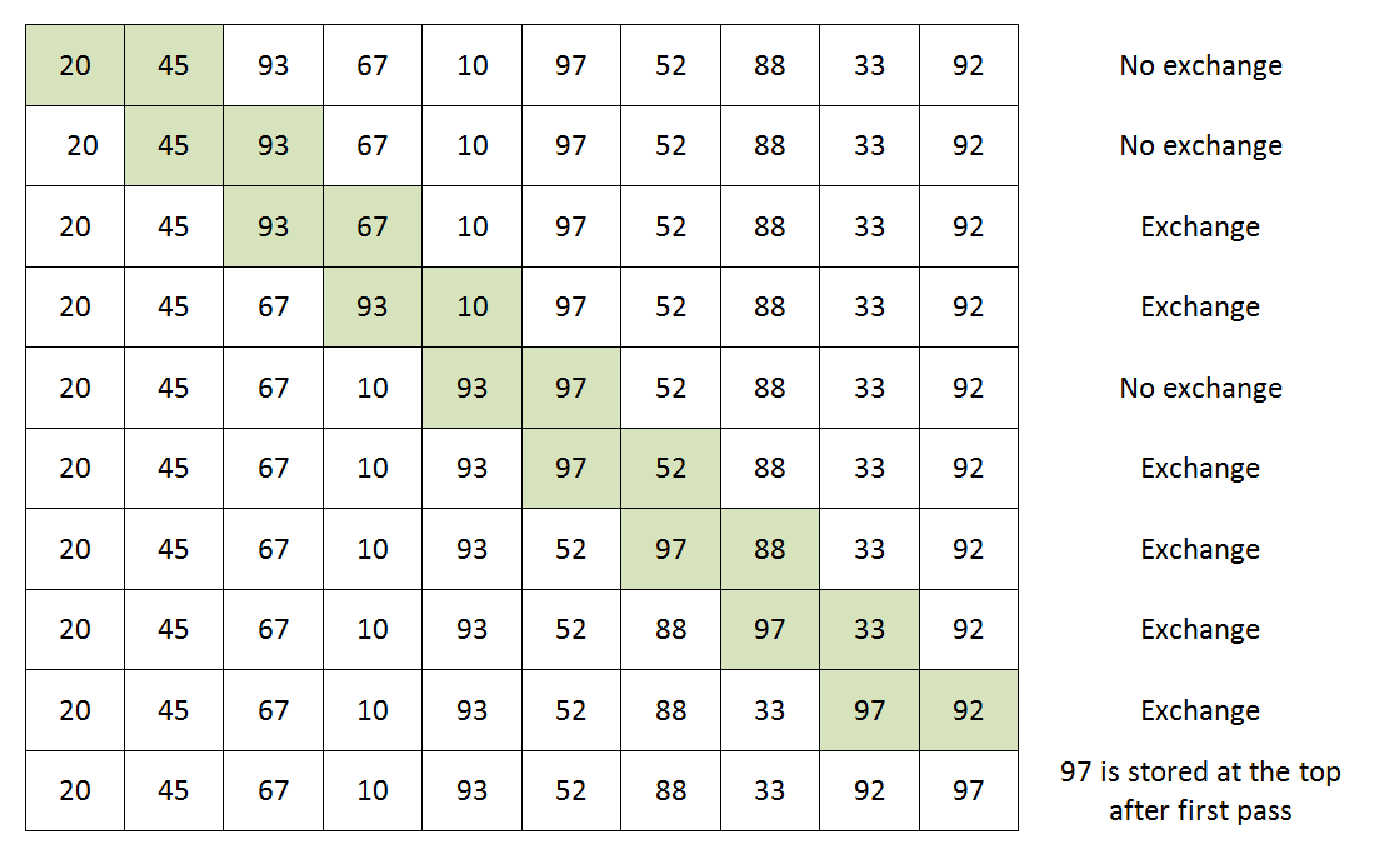
如果我们查看一下前面的图片,就会发现我们正在比较两个数字,然后决定是否交换/互换项目。带背景色的项目表示我们正在比较的两个项目。我们可以看到,外循环的第一次迭代会将最上面的项目存储在列表的最上面。这种情况将持续到我们遍历列表中的每个项目为止。
现在让我们用 PHP 实现冒泡排序算法。
使用 PHP 实现冒泡排序
由于我们假定未排序的数字是在一个列表中,因此我们可以使用 PHP 数组来表示未排序数字的列表。由于数组既有索引又有值,我们可以利用数组轻松地根据位置遍历每个项目,并在适当的地方交换它们。根据我们的伪代码,代码将如下所示:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-02.adoc - include::example$Chapter07/1.php[]我们可以看到,我们使用两个 for 循环遍历每个项目,并与其他项目进行比较。交换是在行中完成的:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-02.adoc - include::example$Chapter07/1.php[]首先,我们将第二个值赋值给一个名为 $tmp 的临时变量。然后,我们将第一个值赋值给第二个值,再将临时值重新赋值给第一个值。这就是所谓的使用第三个变量或临时变量交换两个变量。
只有当第一个值大于第二个值时,我们才进行交换。否则,我们只是忽略。图片右侧的注释显示了交换是否发生。如果我们想按降序排序(较大的数字在前),则只需修改 if 条件如下:
if ($arr[$j] < $arr[$j + 1]) {
}现在,让我们运行代码如下:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-02.adoc - include::example$Chapter07/1.php[]输出结果如下:
10,20,33,45,52,67,88,92,93,97因此,我们可以看到数组是使用冒泡排序算法进行排序的。现在,让我们来讨论一下该算法的复杂性。
冒泡排序的复杂性
在最坏的情况下,第一遍需要进行 n-1 次比较和交换。对于第 n-1 次,在最坏的情况下,我们只需进行一次比较和交换。因此,如果我们一步一步地写,就会发现:
Complexity = n - 1 + n - 2 + ………. + 2 + 1 = n * ( n - 1)/2 = \$O(n^2)\$
因此,冒泡排序的复杂度为 \$O(n^2)\$。不过,在分配临时变量、交换、通过内循环等过程中需要一些恒定时间。我们可以忽略它们,因为它们是常数。
下面是冒泡排序在最佳、平均和最差情况下的时间复杂度表:
最好时间复杂度 |
\$Ω(n)\$ |
最坏时间复杂度 |
\$O(n^2)\$ |
平均时间复杂度 |
\$Θ(n^2)\$ |
空间复杂度(最差情况) |
\$O(1)\$ |
虽然冒泡排序的时间复杂度为 \$O(n^2)\$,但我们仍然可以进行一些改进,以减少比较和交换的次数。现在让我们来探讨一下这些方案。最佳时间为 \$Ω(n)\$,因为我们至少需要运行一个内循环才能发现数组已经排序。
改进冒泡排序算法
冒泡排序最重要的一点是,在外层循环的每次迭代中,至少会有一次交换。如果没有交换,那么列表已经排序完毕。我们可以在伪代码中利用这一改进,并将其重新定义如下:
procedure bubbleSort( A : list of sortable items )
n = length(A)
for i = 1 to n inclusive do
swapped = false
for j = 1 to n-1 inclusive do
if A[j] > A[j+1] then
swap( A[j], A[j+1] )
swapped = true
end if
end for
if swapped is false
break
end if
end for
end procedure我们可以看到,现在我们为每次迭代设置了一个 false 标志,我们希望在内部迭代中,该标志将被设置为 true。如果内循环结束后标志仍为 false,那么我们就可以中断循环,从而将列表标记为已排序。下面是改进版算法的实现:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-02.adoc - include::example$/Chapter07/2.php[]另一个观察结果是,在第一次迭代中,顶层项被置于数组的右侧。在第二个循环中,第二个顶层项将被放在数组右边的第二个单元格中。如果我们能直观地看到,每次迭代后,第 i 个单元格已经存储了排序后的项目,那么就没有必要访问该索引并进行比较。因此,我们可以从内部迭代中减少外部迭代次数,并大大减少比较次数。下面是我们提出的第二种改进方法的伪代码:
procedure bubbleSort( A : list of sortable items )
n = length(A)
for i = 1 to n inclusive do
swapped = false
for j = 1 to n-i-1 inclusive do
if A[j] > A[j+1] then
swap( A[j], A[j+1] )
swapped = true
end if
end for
if swapped is false
break
end if
end for
end procedure现在,让我们用 PHP 来实现最终的改进版本:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-02.adoc - include::example$Chapter07/3.php[]如果我们看一下前面代码中的内循环,唯一的区别是 $j < $len - $i - 1;其他部分与第一次改进相同。因此,基本上,对于我们的 20、45、93、67、10、97、52、88、33、92 列表,我们可以轻松地说,经过第一次迭代后,在第二次迭代比较中将不考虑最前面的数字 97。同样,93 也不会在第三次迭代中被考虑,如下图所示:
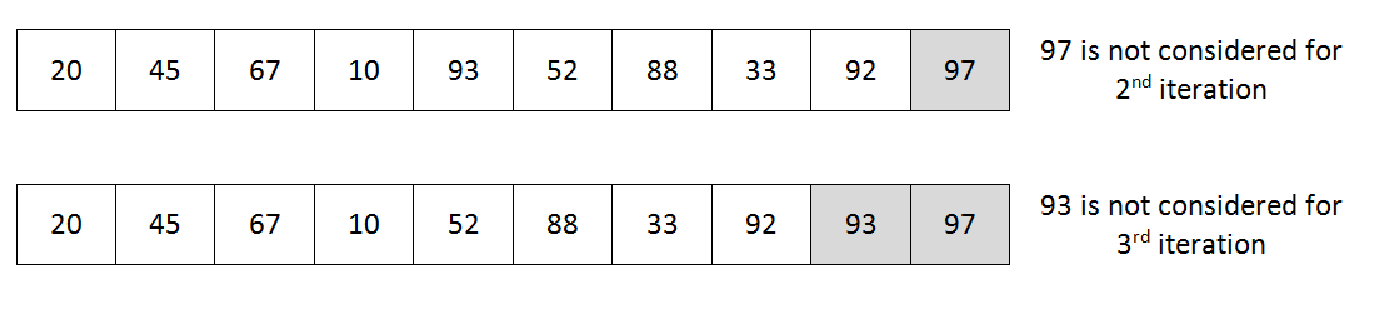
如果我们看一下前面的图片,我们马上会想到一个问题:"92 不是已经排序了吗?难道我们还需要再次比较所有的数字,并在其位置上标出 92 已经排序了吗?是的,我们是对的。这是一个合理的问题。这意味着我们可以知道在内层循环中最后一次交换是在哪个位置进行的;在那之后,数组就已经排序了。因此,我们可以为下一个循环设置一个边界,在此之前,只在我们设置的边界之前进行比较。下面是相关的伪代码:
procedure bubbleSort( A : list of sortable items )
n = length(A)
bound = n -1
for i = 1 to n inclusive do
swapped = false
newbound = 0
for j = 1 to bound inclusive do
if A[j] > A[j+1] then
swap( A[j], A[j+1] )
swapped = true
newbound = j
end if
end for
bound = newbound
if swapped is false
break
end if
end for
end procedure在这里,我们在完成每个内循环后设置绑定,确保不会进行不必要的迭代。下面是使用前面的伪代码编写的实际 PHP 代码:
Unresolved include directive in modules/ROOT/pages/ch07/ch7-02.adoc - include::example$Chapter07/4.php[]我们看到过不同的冒泡排序实现,但输出结果总是一样的:10、20、33、45、52、67、88、92、93、97。如果是这样的话,我们怎么能确定我们的改进确实对算法产生了一些影响呢?下面是我们对初始列表 20、45、93、67、10、97、52、88、33、92 的所有四种实现进行比较的次数统计:
| 解决 | 比较次数 |
|---|---|
正常冒泡排序 |
90 |
第一次提升 |
63 |
第二次提升 |
42 |
第三次提升 |
38 |
我们可以看到,通过我们的改进,比较次数从 90 次减少到了 38 次。因此,我们当然可以通过一些改进来提高算法的性能,从而减少所需的比较次数。