树的定义和属性

树是由节点或顶点组成的、由边连接的层次集合。树不能循环，节点与其下级节点或子节点之间只存在边。同一父节点的两个子节点之间不能有任何边。每个节点都可以有一个父节点，但顶层节点除外，顶层节点也称为根节点。每棵树只能有一个根节点。每个节点可以有零个或多个子节点。在下图中，A 是根节点，B、C 和 D 是 A 的子节点。我们也可以说 A 是 B、C 和 D 的父节点：

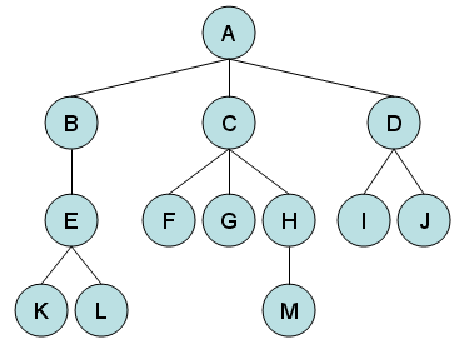
image 2023 11 08 08 32 43 670

没有任何子节点的节点称为叶节点。在上图中，K、L、F、G、M、I 和 J 是叶节点。叶节点也称为外部节点或终端节点。除根节点外，至少有一个子节点的节点称为内部节点。这里，B、C、D、E 和 H 是内部节点。下面是我们在描述树形数据结构时使用的其他一些常用术语：

  • 子节点(Descendent)：这是一个可以从父节点通过重复过程到达的节点。例如，上图中的 M 是 C 的后代。

  • 祖节点(Ancestor)：这是从子节点到父节点可以通过重复方式到达的节点。例如，B 是 L 的祖先。

  • 度数(Degree)：某个父节点的子节点总数称为其度。在我们的例子中，A 的阶数为 3，B 的阶数为 1，C 的阶数为 3，D 的阶数为 2。

  • 路径(Path)：从源节点到目标节点的节点和边的序列称为两个节点之间的路径。路径的长度就是路径中节点的数量。在我们的例子中，A 到 M 之间的路径为 A-C-H-M，路径长度为 4：

    image 2023 11 08 08 36 54 683

  • 节点高度(Height of node)：节点的高度由节点与下级节点最深层级之间的边数定义。例如，节点 B 的高度为 2。

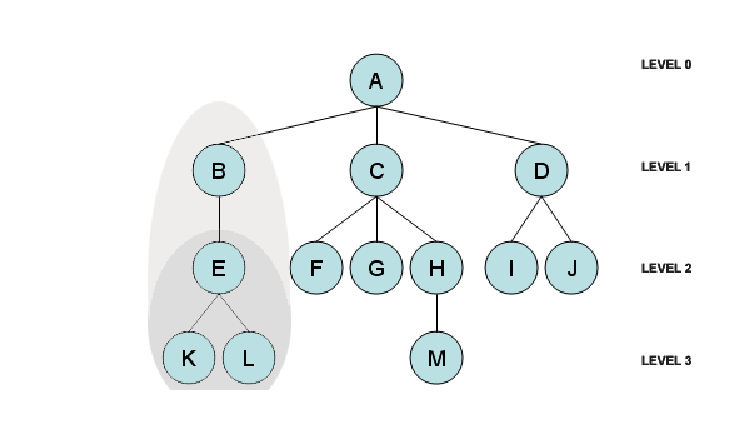
  • 级别(Level)：级别代表节点的生成。如果父节点处于第 n 层，其子节点将处于第 n+1 层。因此，级别是由节点和根节点之间的边数 1+ 来定义的。这里：

    • 根 A 处于级别 0

    • B、C 和 D 属于 1 级

    • E、F、G、H、I 和 J 处于 2 级

    • K、L 和 M 处于 3 级

  • 树的高度(Height of tree)：树的高度由根节点的高度决定。这里，树的高度是 3。

  • 子树(Subtree)：在树形结构中，每个子节点都会递归形成一个子树。换句话说，一棵树由许多子树组成。例如，B 与 E、K 和 L 组成子树，而 E 与 K 和 L 组成子树。我们也可以对 C 和 D 及其子树做同样的处理。

  • 深度(Depth)：节点的深度由节点与根节点之间的边数决定。例如，在我们的树图像中，H 的深度为 2，L 的深度为 3。

  • 森林(Forest)：森林是由零棵或多棵不相交的树组成的集合。

  • 遍历(Traverse)：这表示按照特定顺序访问节点的过程。我们将在接下来的章节中经常使用这个术语。

  • 键(Keys)：键是节点中的一个值，用于搜索目的。