二分查找

二进制搜索是编程界非常流行的一种搜索算法。在顺序搜索中，我们从头开始，逐项扫描，以找到所需的项目。但是，如果列表已经排序，那么我们就不需要从列表的开头或结尾开始搜索。在二进制搜索算法中，我们从列表的中间开始，检查中间的项目是小于还是大于我们要找的项目，然后决定走哪条路。这样，我们就会将列表分成两半，并完全丢弃其中的一半，就像下图一样：

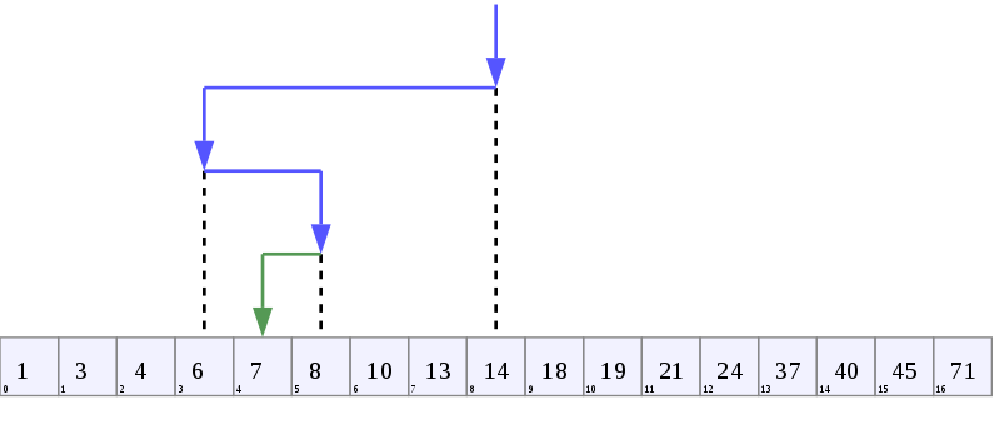
请看上图，数组中有一个已排序（升序）的数字列表。我们想知道第 7 项是否在数组中。由于数组有 17 个项目（0 至 16 索引），我们将首先查找中间的索引，也就是本例中的第 8 个索引。现在，第八索引的值是 14，大于我们要查找的值 7。这意味着如果数组中存在 7，那么它就在 14 的左边，因为数字已经排序。因此，我们放弃从第 8 个索引到第 16 个索引的数组，因为数字不可能出现在数组的这一部分。现在，我们重复同样的过程，取数组剩余部分的中间值，即剩余部分的第三个元素。现在，第三个元素的值是 6，小于 7。因此，我们要查找的项目位于第三个元素的右侧，而不是左侧。

现在，我们将检查数组的第四个元素到第七个元素，中间的元素现在指向第五个元素。第五个元素的值是 8，大于我们要找的 7。因此，我们必须考虑第五元素的左侧，才能找到我们要找的项目。这一次，数组只剩下两个要检查的项目，分别是第四和第五元素。当我们向左移动时，我们将检查第四个元素，我们看到值与我们正在寻找的 7 相匹配。如果第四个索引值不是 7，函数将返回 false，因为已经没有元素需要检查了。如果我们看一下上图中的箭头标记，就会发现只用了四步，我们就找到了我们要找的值，而在最坏的情况下，我们不得不用线性搜索函数走 17 步来检查所有 17 个数字。这就是所谓的二进制搜索，或半区间搜索，或对数搜索。

正如我们在上一张图片中看到的，我们必须将初始列表分成两半，然后继续下去，直到我们无法再进行任何分割来找到我们的项目为止。我们可以使用迭代法或递归法来执行分割部分。实际上，我们两种方式都会用到。因此，让我们先用迭代方式定义二进制搜索的伪代码：

BinarySearch(A : list of sorted items, value) {
    low = 0
    high = N
    while (low <= high) {
        // lowest int value, no fraction
        mid = (low + high) / 2
        if (A[mid] > value)
          high = mid - 1
        else if (A[mid] < value)
          low = mid + 1
        else
          return true
    }
    return false
}

如果我们看一下伪代码，就会发现我们是根据中间值来调整下限和上限的。如果我们寻找的值大于中间值，我们就会将下限调整为 mid+1。如果小于中间值，那么我们就会将较高值设为 mid-1。这个过程一直持续到下限值大于上限值或找到项目为止。如果未找到项目，则在函数结束时返回 false。现在，让我们用 PHP 来实现这个伪代码：

Unresolved include directive in modules/ROOT/pages/ch08/ch8-02.adoc - include::example$Chapter08/2.php[]

在实现过程中，我们遵循了前一页中的大部分伪代码。现在，让我们用两次搜索来运行代码，我们知道一个值在列表中，另一个不在列表中：

Unresolved include directive in modules/ROOT/pages/ch08/ch8-02.adoc - include::example$Chapter08/2.php[]

我们从之前的线性搜索代码中得知，31 在列表中，应该显示 Found。但是，500 不在列表中，应该显示 Not found。如果我们运行代码，我们将在控制台看到以下输出：

31 Found
500 Not found

现在我们将编写二进制搜索的递归算法，这对我们来说也很方便。伪代码要求我们每次调用函数时都发送额外的参数。我们需要在每次递归调用时发送低值和高值，而在迭代调用时我们并没有这样做：

BinarySearch(A : list of sorted items, value, low, high) {
    if (high < low)
        return false

        // lowest int value, no fraction
        mid = (low + high) / 2

        if (A[mid] > value)
            return BinarySearch(A, value, low, mid - 1)
        else if (A[mid] < value)
            return BinarySearch(A, value, mid + 1, high)
    else
        return TRUE;
}

从前面的伪代码中我们可以看到，现在我们将 low 和 high 作为参数，在每次调用中，新值都会作为参数发送。我们还有一个边界条件，即检查低值是否大于高值。与迭代代码相比，该代码看起来更小更简洁。现在，让我们用 PHP 7 来实现它：

Unresolved include directive in modules/ROOT/pages/ch08/ch8-02.adoc - include::example$Chapter08/3.php[]

现在，让我们使用以下代码递归地运行此搜索：

Unresolved include directive in modules/ROOT/pages/ch08/ch8-02.adoc - include::example$Chapter08/3.php[]

从前面的代码中我们可以看到，在递归二进制搜索的每次调用中，我们都会首次发送 0 和 count($numbers)-1。然后，每次递归调用都会根据中间值自动调整高低值。因此，我们看到了二进制搜索的迭代和递归实现。根据需要，我们可以在程序中使用其中任何一种。现在，让我们分析一下二进制搜索算法，看看它比线性或顺序搜索算法好在哪里。

二分查找算法分析

到目前为止，我们已经看到，每次迭代时，我们都会将列表除以一半，并完全丢弃一半进行搜索。这样，经过 1 次、2 次和 3 次迭代后，我们的列表看起来分别是 n/2、n/4、n/8，以此类推。因此，我们可以说，经过 K 次迭代后，将剩下 n/2^k 个条目。我们可以很容易地说，最后一次迭代发生在 n/2^k = 1 时，或者我们可以说，2^K = n。因此，对两边取对数得出 k = \$log(n)\$，这是二进制搜索算法最坏情况下的运行时间。下面是二进制搜索算法的复杂度：

最好时间复杂度

\$O(1)\$

最坏时间复杂度

\$O(logn)\$

平均时间复杂度

\$O(logn)\$

空间复杂度（最差情况）

\$O(1)\$

如果我们的数组或列表已经排序，则最好使用二进制搜索以获得更好的性能。现在，无论列表是按升序还是降序排序，都会对我们计算低值和高值产生一些影响。我们目前看到的逻辑是升序排序。如果数组按降序排序，逻辑将发生变化，大于将变为小于，反之亦然。这里需要注意的一点是，二进制搜索算法会为我们提供搜索项的索引。但是，在某些情况下，我们不仅需要知道数字是否存在，还需要找到它在列表中的第一次出现或最后一次出现。如果我们使用二进制搜索算法，那么它将返回 "true" 或最大索引号，即搜索算法在其中找到的数字。但是，这可能不是第一次出现或最后一次出现。为此，我们将对二进制搜索算法稍作修改，称之为重复二进制搜索树算法。

重复二叉搜索树算法

请看下图。我们有一个包含重复项的数组。如果我们试图从数组中找出第一次出现的 2，上一节的二进制搜索算法会给出第五个元素。然而，从下图中我们可以清楚地看到，它不是第五个元素，而是第二个元素，这才是正确答案。因此，我们需要修改二进制搜索算法。这种修改就是重复搜索，直到找到第一个出现的元素：

这是使用迭代方法的修改后的解决方案：

Unresolved include directive in modules/ROOT/pages/ch08/ch8-02.adoc - include::example$Chapter08/4.php[]

正如我们所看到的，首先我们要检查中间是否有我们要查找的值。如果为真，那么我们就将中间的索引指定为首次出现的索引，然后搜索中间元素的左侧，检查是否有我们要找的数字出现。然后继续迭代，直到搜索完每个索引（$low 大于 $high）。如果没有找到其他出现的数字，那么变量 first occurrence 的值将是我们找到该项的第一个索引的值。如果没有，我们将像往常一样返回 -1。让我们运行下面的代码来检查结果是否正确：

Unresolved include directive in modules/ROOT/pages/ch08/ch8-02.adoc - include::example$Chapter08/4.php[]

现在，我们有一个重复值为 2、3、4 和 5 的数组。我们想搜索数组，找到数值首次出现的位置或索引。例如，如果我们在一个普通的二进制搜索函数中搜索 2，它将返回第八个作为找到值 2 的位置。而在我们的例子中，我们实际上是在查找第二个索引，它实际上是项目 2 第一次出现的位置。我们的函数 repetitiveBinarySearch 正是这样做的，我们将返回位置存储到一个名为 $pos 的变量中。如果找到了数字和位置，我们就会显示输出结果。现在，如果我们在控制台中运行前面的代码，就会得到以下输出结果：

2 Found at position 1
5 Found at position 16

这符合我们的预期结果。因此，我们可以说，我们现在有了一种重复的二进制搜索算法，可以从给定的排序列表中找到项目的首次和最后一次出现。这可能是一个非常方便的函数，可以解决很多问题。

到目前为止，从我们的示例和分析中，我们可以得出结论：二进制搜索肯定比线性搜索快。不过，应用二进制搜索的主要前提是先对列表进行排序。在未排序的数组中应用二进制搜索会导致我们得到不准确的结果。在某些情况下，我们会收到一个数组，但不确定该数组是否已排序。现在的问题是："在这种情况下，我们是否应该先对数组进行排序，然后再应用二进制搜索算法？还是应该直接运行线性搜索算法来查找项目？让我们来讨论一下这个问题，以便知道如何处理这种情况。

搜索未排序的数组 - 我们应该先排序吗？

因此，我们现在的情况是，数组中有 n 个项目，而且没有排序。由于我们知道二进制搜索的速度更快，所以我们决定先排序，然后使用二进制搜索查找项。如果这样做，我们必须记住，最好的排序算法的最坏时间复杂度为 \$O(nlog n)\$，而二进制搜索的最坏复杂度为 \$O(log n)\$。因此，如果我们先进行排序，然后再应用二进制搜索，复杂度将是 \$O(n log n)\$，因为与 \$O(log n)\$ 相比，二进制搜索的复杂度最大。不过，我们也知道，对于任何线性或顺序搜索（已排序或未排序），最坏情况下的时间复杂度都是 \$O(n)\$，比 \$O(n log n)\$ 要好得多。

根据 \$O(n)\$ 和 \$O(n log n)\$ 的复杂度比较，我们可以明确地说，如果数组没有排序，执行线性搜索是更好的选择。

让我们考虑另一种情况，即我们需要对给定数组进行多次搜索。我们用 k 表示搜索数组的次数。如果 k 为 1，那么我们可以很容易地应用上一段讨论的线性方法。如果 k 的值小于数组的大小（用 n 表示），那就没问题。但是，如果 k 的值接近或大于 n，那么我们在这里应用线性方法就会遇到一些问题。

假设 k = n，那么在 n 时间内，线性搜索的复杂度为 \$O(n^2)\$。现在，如果我们采用先排序后搜索的方法，那么即使 k 再大，一次性排序也需要 \$O(n log n)\$ 的时间复杂度。然后，每次搜索将耗时 \$O(log n)\$，n 次搜索的最坏情况复杂度为 \$O(n log n)\$。如果从最坏的运行情况出发，我们对 k 个项目进行排序和搜索的复杂度为 \$O(n log n)\$，这比顺序搜索要好。

因此，我们可以得出这样的结论：如果搜索操作的次数与数组的大小相比较少，那么最好不要对数组进行排序，而是执行顺序搜索。但是，如果搜索操作的次数与数组的大小相比较多，则最好先对数组进行排序，然后再应用二进制搜索。

多年来，二进制搜索算法不断发展，出现了不同的变体。与其每次都选择中间索引，我们可以通过计算来决定下一步应该使用哪个索引。这就是这些变体能高效工作的原因。下面我们将讨论二进制搜索算法的两种变体：插值搜索和指数搜索。