使用布隆过滤器和稀疏矩阵
稀疏矩阵是一种高效的数据结构。稀疏矩阵的 0 值比实际值多。例如,一个 100 X 100 的矩阵可能有 10,000 个单元格。现在,在这 10,000 个单元格中,只有 100 个单元格有数值,其余的都是 0。除了这 100 个数值外,其余的单元格都被默认值 0 占用,而且它们需要相同大小的字节来存储表示空单元格的数值 0。这极大地浪费了空间,我们可以使用稀疏矩阵来减少空间。我们可以使用不同的技术,将稀疏矩阵的值存储在一个单独的矩阵中,这样会非常精简,不会占用任何不必要的空间。我们也可以使用链接列表来表示稀疏矩阵。下面是稀疏矩阵的一个示例:
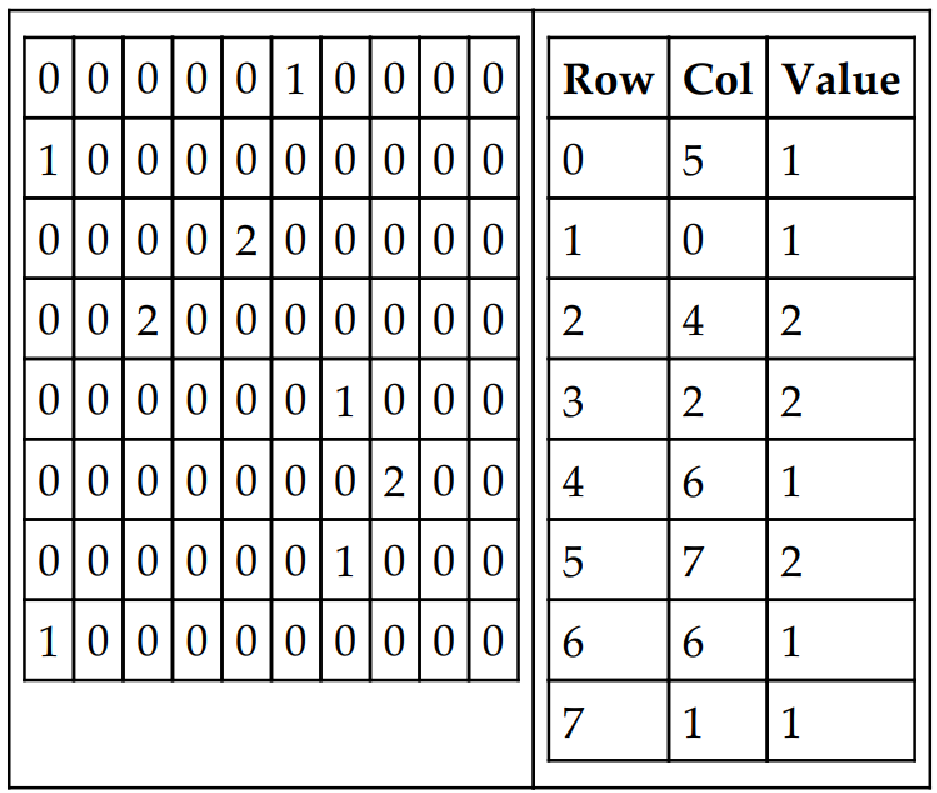
由于 PHP 数组的性质是动态的,因此在 PHP 中处理稀疏矩阵的最佳方法是只使用有值的索引,而不使用其他索引。在使用单元格时,我们可以检查该单元格是否有值,否则就使用默认值 0,如下例所示:
Unresolved include directive in modules/ROOT/pages/ch11/ch11-12.adoc - include::example$Chapter11/11.php[]这将在命令行中产生以下输出:
0
1
0当我们拥有一个庞大的数据集时,在数据集中进行查找可能会非常耗时和昂贵。假设我们有一个包含 1 000 万个电话号码的数据集,我们想搜索某个电话号码。这可以通过数据库查询轻松完成。但是,如果是 10 亿个电话号码呢?从数据库中查找还会更快吗?如此庞大的数据库会造成查找速度缓慢。为了解决这个问题,一种有效的方法是使用 Bloom 过滤器。
bloom 过滤器是一种空间效率高的概率数据结构,它能确定特定项目是否属于一个集合。它返回两个值: "可能在集合中 "和 "肯定不在集合中"。如果某个项目不属于某个集合,则 bloom 过滤器返回 false。但是,如果返回值为 true,则该项目可能在集合中,也可能不在集合中。这里将介绍其中的原因。
一般来说,bloom 过滤器是一个大小为 m 的比特数组,其中所有的初始值都为 0。哈希值可以在 0 到 m 之间,因为 m 是比特数组的最大大小。哈希函数类似于 md5、sha1、crc32 等,但它们非常快速高效。通常,在 bloom filter fnv、murmur、Siphash 等程序中都会使用哈希函数。以初始值为 0 的 16(16+1 个单元)比特 bloom 过滤器为例:

假设我们有两个哈希函数 k1 和 k2,用于将项目转换为 0 到 16 之间的整数值。让我们在 Bloom 过滤器中存储的第一个项目是 "PHP"。那么,我们的哈希函数将返回以下结果:
k1("PHP") = 5
k2("PHP") = 9两个哈希函数返回了两个不同的值。现在我们可以在位数组中放 1 来标记。比特数组现在看起来是这样的:

现在,让我们在列表中添加另一个项目,例如 "算法"。假设我们的哈希函数将返回以下值:
k1("algorithm") = 2
k2("algorithm") = 5由于我们可以看到 5 已被另一个项目标记,因此无需再次标记。现在,比特数组看起来是这样的:

例如,现在我们要检查名为 "error" 的项目,它的散列值如下:
k1("error") = 2
k2("error") = 9我们可以看到,我们的哈希函数 k1 和 k2 返回了字符串 "error" 的哈希值,而这个字符串在数组中并不存在。因此,这肯定是一个错误,如果我们的哈希函数数量很少,就会出现这样的错误。散列函数越多,错误就越少,因为不同的散列函数会返回不同的值。错误率、哈希函数的数量和 Bloom 过滤器的大小之间存在一定的关系。例如,一个包含 5000 个项目、错误率为 0.0001 的 Bloom 过滤器大约需要 14 个散列函数和 96000 个比特。我们可以从在线 bloomfilter 计算器(如 https://krisives.github.io/bloom-calculator/ )中获得这些数据。