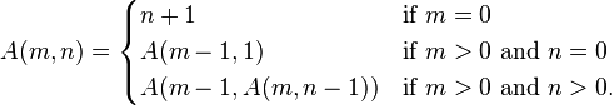不同类型的递归

线性递归是编程世界中最常用的递归之一。当函数每次运行都调用自身一次时，我们称之为线性递归。就像我们的阶乘例子一样，当我们将大计算分解成小计算，直到达到基本条件时，我们称之为缠绕(winding)。当我们从基本条件返回到第一次递归调用时，我们称之为解卷。我们将在本章接下来的章节中学习不同的线性递归。

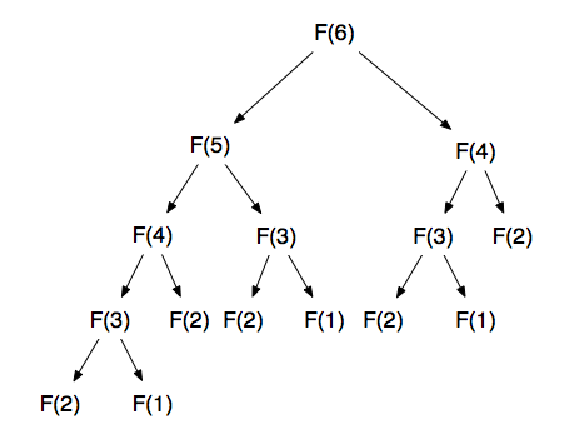
在二进制递归中，函数每次运行都会调用自身两次。因此，计算结果取决于对自身的两次不同递归调用的两个结果。如果我们看一下斐波那契数列生成递归函数，就不难发现这是一个二进制递归函数。除此之外，我们在编程世界中还有许多常用的二进制递归，如二进制搜索、分而治之、合并排序等。下图显示的就是二进制递归：

当返回时没有待执行操作时，递归方法就是尾递归。例如，在我们的阶乘代码中，返回值用于与前一个值相乘来计算阶乘。因此，这不是尾递归。斐波那契数列递归也是如此。如果我们看一下 GCD 递归，就会发现在返回值之后没有任何操作。因此，最终返回或基例返回实际上就是答案。因此，GCD 就是尾递归的一个例子。尾递归也是线性递归的一种形式。

我们可能需要以另一种方式从两个不同的方法递归调用两个不同的方法。例如，函数 A() 在每次调用时都会调用函数 B()，而函数 B() 在每次调用时都会调用函数 A()。这就是所谓的相互递归。

如果递归函数调用的参数是自身，则称为嵌套递归。嵌套递归的常见例子之一是阿克曼函数。请看下面的公式：

如果我们看最后一行，就会发现函数 A() 是递归调用的，但第二个参数本身又是另一个递归调用。因此，这就是嵌套递归的例子之一。

虽然递归类型多种多样，但我们只会根据需要使用其中的一种。现在，我们来看看递归在项目中的实际应用。