何谓算法分析
刚接触计算机科学的同学常常拿自己的程序和别人的做比较。你可能已经注意到了,计算机程序看起来很相似,尤其是简单的程序。这就产生了一个有趣的问题:当两个看上去不同的程序解决同一个问题时,会有优劣之分么?
要回答这个问题,需要记住,程序和它所代表的算法是不同的。第 1 章说过,算法是为逐步解决问题而设计的一系列通用指令。给定某个输入,算法能得到对应的结果——算法就是解决问题的方法。程序则是用某种编程语言对算法编码。同一个算法可以对应许多程序,这取决于程序员和编程语言。
为了进一步说明算法和程序的区别,来看看代码清单 2-1 中的函数。该函数解决了一个常见的问题,即计算前 n 个整数之和。算法的思路是使用一个初始值为 0 的累加器变量,然后遍历 n 个整数,并将值加到累加器上。
def sumOfN(n):
theSum = 0
for i in range(1,n+1):
theSum = theSum + i
return theSum
print(sumOfN(10))下面看看代码清单2-2。乍看会觉得有些奇怪,但是仔细观察后,你会发现这个函数所做的工作在本质上和前一个相同。之所以不能一眼看出来,是因为代码写得太差。没有用好的变量名提高可读性,而且在累加时还使用了一条多余的赋值语句。
def foo(tom):
fred = 0
for bill in range(1,tom+1):
barney = bill
fred = fred + barney
return fred
print(foo(10))前面提出过一个问题:程序是否有优劣之分?答案取决于你的标准。如果你关心的是可读性,那么 sumOfN 当然比 foo 更好。实际上,你可能已经在编程入门课上看过很多例子,毕竟入门课的一个目标就是帮你写出易读的程序。不过,除了可读性,本书还对描述算法感兴趣。(我们当然希望你继续向着写出易读代码的目标努力。)
算法分析关心的是基于所使用的计算资源比较算法。我们说甲算法比乙算法好,依据是甲算法有更高的资源利用率或使用更少的资源。从这个角度来看,上面两个函数其实差不多,它们本质上都利用同一个算法解决累加问题。
计算资源究竟指什么?思考这个问题很重要。有两种思考方式。一是考虑算法在解决问题时要占用的空间或内存。解决方案所需的空间总量一般由问题实例本身决定,但算法往往也会有特定的空间需求,后文会详细介绍。
另一种思考方式是根据算法执行所需的时间进行分析和比较。这个指标有时称作算法的执行时间或运行时间。要衡量 sumOfN 函数的执行时间,一个方法就是做基准分析。也就是说,我们会记录程序计算出结果所消耗的实际时间。在 Python 中,我们记录下函数就所处系统而言的开始时间和结束时间。time 模块中有一个 time 函数,它会以秒为单位返回自指定时间点起到当前的系统时钟时间。在首尾各调用一次这个函数,计算差值,就可以得到以秒为单位的执行时间(多数情况下非常短)。
在代码清单2-3 中,sumOfN 函数在累加前后调用 time。函数返回一个元组,由结果与计算时间(单位为秒)构成。如果调用 5 次,每次计算前 10000 个整数之和,会得到如下结果。
>>> for i in range(5):
print("Sum is %d required %10.7f seconds" % sumOfN(10000))
Sum is 50005000 required 0.0018950 seconds
Sum is 50005000 required 0.0018620 seconds
Sum is 50005000 required 0.0019171 seconds
Sum is 50005000 required 0.0019162 seconds
Sum is 50005000 required 0.0019360 seconds
>>>import time
def sumOfN2(n):
start = time.time()
theSum = 0
for i in range(1,n+1):
theSum = theSum + i
end = time.time()
return theSum,end-start可以看出,执行时间基本上是一致的,平均约为0.0019秒。如果计算前 100000 个整数之和,又会如何呢?
>>> for i in range(5):
print("Sum is %d required %10.7f seconds" % sumOfN(100000))
Sum is 5000050000 required 0.0199420 seconds
Sum is 5000050000 required 0.0180972 seconds
Sum is 5000050000 required 0.0194821 seconds
Sum is 5000050000 required 0.0178988 seconds
Sum is 5000050000 required 0.0188949 seconds
>>>执行时间都变长了,但还是很一致,差不多都是之前的 10 倍。如果 n 取 1000000,结果如下。
>>> for i in range(5):
print("Sum is %d required %10.7f seconds" % sumOfN(1000000))
Sum is 500000500000 required 0.1948988 seconds
Sum is 500000500000 required 0.1850290 seconds
Sum is 500000500000 required 0.1809771 seconds
Sum is 500000500000 required 0.1729250 seconds
Sum is 500000500000 required 0.1646299 seconds
>>>这次的平均执行时间差不多是前一个例子的 10 倍。
现在来看看代码清单2-4,其中给出了解决累加问题的新方法。函数 sumOfN3 使用以下公式计算前 n 个整数之和,不必使用循环。
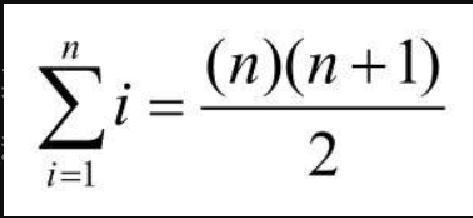
def sumOfN3(n):
return (n*(n+1))/2
print(sumOfN3(10))对 sumOfN3 做同样的基准测试,n 取 5 个值(10000、100000、1000000、10000000 和 100000000),会得到以下结果。
Sum is 50005000 required 0.00000095 seconds
Sum is 5000050000 required 0.00000191 seconds
Sum is 500000500000 required 0.00000095 seconds
Sum is 50000005000000 required 0.00000095 seconds
Sum is 5000000050000000 required 0.00000119 seconds关于这个结果,有两点要注意。首先,记录的耗时比之前的例子都要短。其次,不管 n 取什么值,耗时都很稳定。看起来 sumOfN3 不太受整数数目的影响。
不过,以上基准测试结果的意义到底是什么呢?直觉上,循环方案看上去工作量更大,因为有些步骤重复。这好像是耗时更久的原因。而且,循环方案的耗时会随着n一起增长。然而,这里有个问题。如果在另一台计算机上运行这个函数,或用另一种编程语言来实现,很可能会得到不同的结果。如果计算机再旧些, sumOfN3 的执行时间甚至更长。
所以,我们需要更好的方式来描述算法的执行时间。基准测试计算的是执行算法的实际时间。这不是一个有用的指标,因为它依赖于特定的计算机、程序、时间、编译器与编程语言。我们希望找到一个独立于程序或计算机的指标。这样的指标在评价算法方面会更有用,可以用来比较不同实现下的算法。
大\$O\$记法
试图摆脱程序或计算机的影响而描述算法的效率时,量化算法的操作或步骤很重要。如果将每一步看成基本计算单位,那么可以将算法的执行时间描述成解决问题所需的步骤数。确定合适的基本计算单位很复杂,也依赖于算法的实现。
对于累加算法,计算总和所用的赋值语句的数目就是一个很好的基本计算单位。在 sumOfN 函数中,赋值语句数是 1(theSum = 0)加上 n(theSum = theSum + i 的运行次数)。可以将其定义成函数 T,令 \$T(n)\$=1+n。参数 n 常被称作问题规模,可以将函数解读为 “当问题规模为 n 时,解决问题所需的时间是 \$T(n)\$,即需要 1+n 步”。
在前面给出的累加函数中,用累加次数定义问题规模是合理的。这样一来,就可以说处理前 100000 个整数的问题规模比处理前 1000 个整数的大。鉴于此,前者花的时间要比后者长。接下来的目标就是揭示算法的执行时间如何随问题规模而变化。
计算机科学家将分析向前推进了一步。精确的步骤数并没有 \$T(n)\$ 函数中起决定性作用的部分重要。也就是说,随着问题规模的增长,\$T(n)\$ 函数的某一部分会比其余部分增长得更快。最后比较的其实就是这一起决定性作用的部分。数量级函数描述的就是,当 n 增长时,\$T(n)\$ 增长最快的部分。数量级(order of magnitude)常被称作大 \$O\$ 记法( \$O\$ 指 order),记作 \$O(f(n))\$。它提供了步骤数的一个有用的近似方法。\$f(n)\$ 函数为 \$T(n)\$ 函数中起决定性作用的部分提供了简单的表示。
对于 \$T(n)\$=1+n,随着 n 越来越大,常数 1 对最终结果的影响越来越小。如果要给出 \$T(n)\$ 的近似值,可以舍去 1,直接说执行时间是 \$O(n)\$。注意,1 对于 \$T(n)\$ 来说是重要的。但是随着 n 的增长,没有 1 也不会太影响近似值。
再举个例子,假设某算法的步骤数是 \$T(n)=5n^2+27n+1005\$。当 n 很小时,比如说 1 或 2,常数 1005 看起来是这个函数中起决定性作用的部分。然而,随着 n 增长,n2 变得更重要。实际上,当 n 很大时,另两项的作用对于最终结果来说就不显著了,因此可以忽略这两项,只关注5n2。另外,当 n 变大时,系数 5 的作用也不显著了。因此可以说,函数 \$T(n)\$ 的数量级是 \$f(n)=n^2\$,或者直接说是 \$O(n^2)\$。
累加的例子没有体现的一点是,算法的性能有时不仅依赖于问题规模,还依赖于数据值。对于这种算法,要用最坏情况、最好情况和普通情况来描述性能。最坏情况指的是某一个数据集会让算法的性能极差;另一个数据集可能会让同一个算法的性能极好(最好情况)。大部分情况下,算法的性能介于两个极端之间(普通情况)。计算机科学家要理解这些区别,以免被某个特例误导。
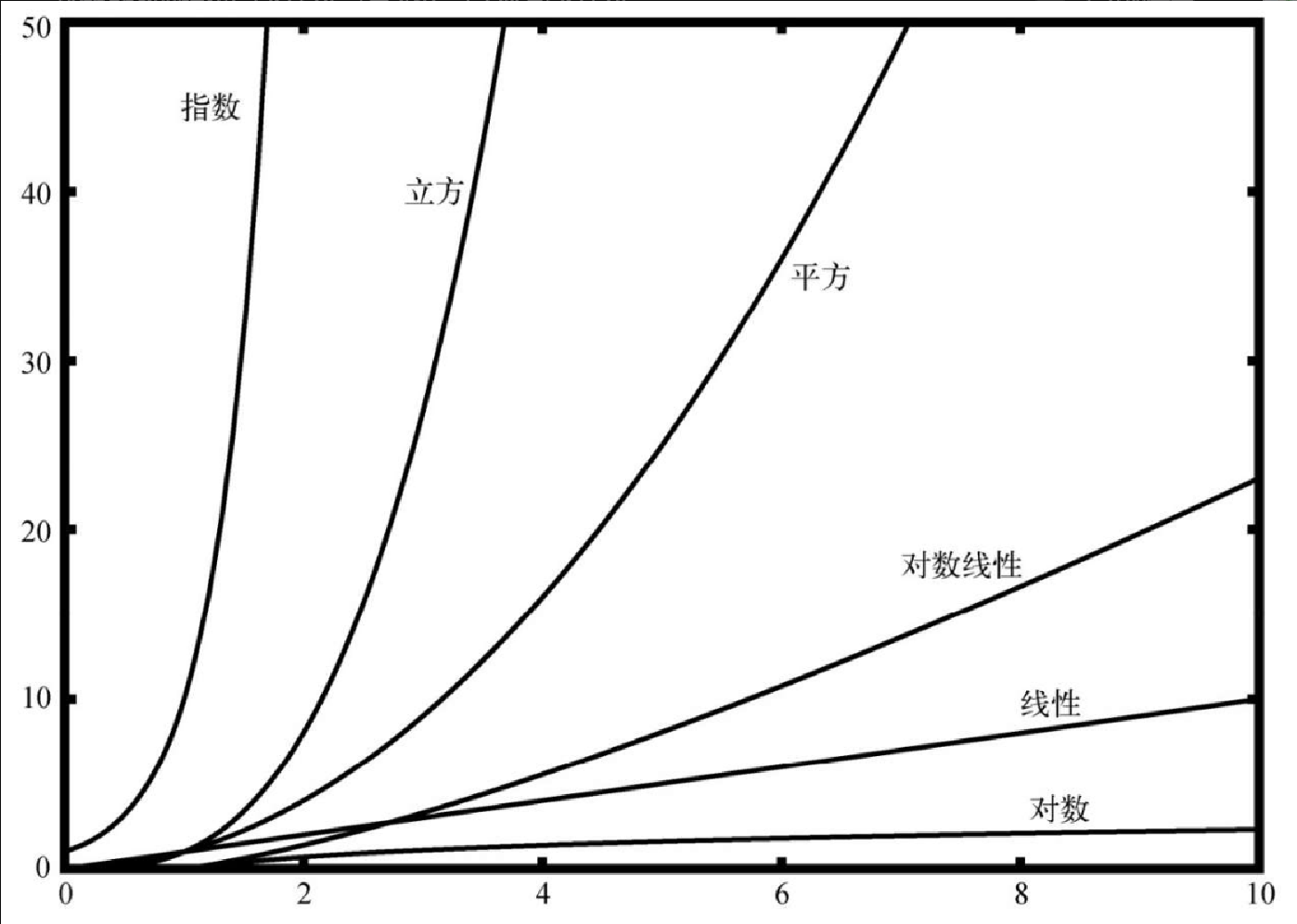
在学习算法的路上,常见的函数会反复出现,如表2-1所示。要判断哪一个才是 \$T(n)\$ 的决定性部分,必须了解它们在 n 变大时彼此有多大差别。图2-1展示了表2-1 中的各个函数。注意,当 n 较小时,这些函数之间的界限不是很明确,很难看出哪个起主导作用。随着 n 的增长,它们之间的差别就很明显了。

最后来看一个例子,假设有如代码清单2-5 所示的一段 Python 代码。尽管这个程序没有做什么实际工作,但它对分析性能有一定的指导意义。
a=5
b=6
c=10
for i in range(n):
for j in range(n):
x = i * i
y = j * j
z = i * j
for k in range(n):
w = a*k + 45
v = b*b
d = 33赋值操作的数量是 4 项之和:\$T(n)=3+3n^2+2n+1\$。第 1 项是常数 3,对应起始部分的 3 条赋值语句。第 2 项是3n2,因为有 3 条语句要在嵌套循环中重复 n2 次。第 3 项是 2n,因为两条语句要循环 n 遍。第 4 项是常数 1,代表最后那条赋值语句。
\$T(n)=3+3n^2+2n+1=3n^2+2n+4\$
很容易看出来,n2 起主导作用,所以这段代码的时间复杂度是 \$O(n^2)\$。当 n 变大时,其他项以及主导项的系数都可以忽略。
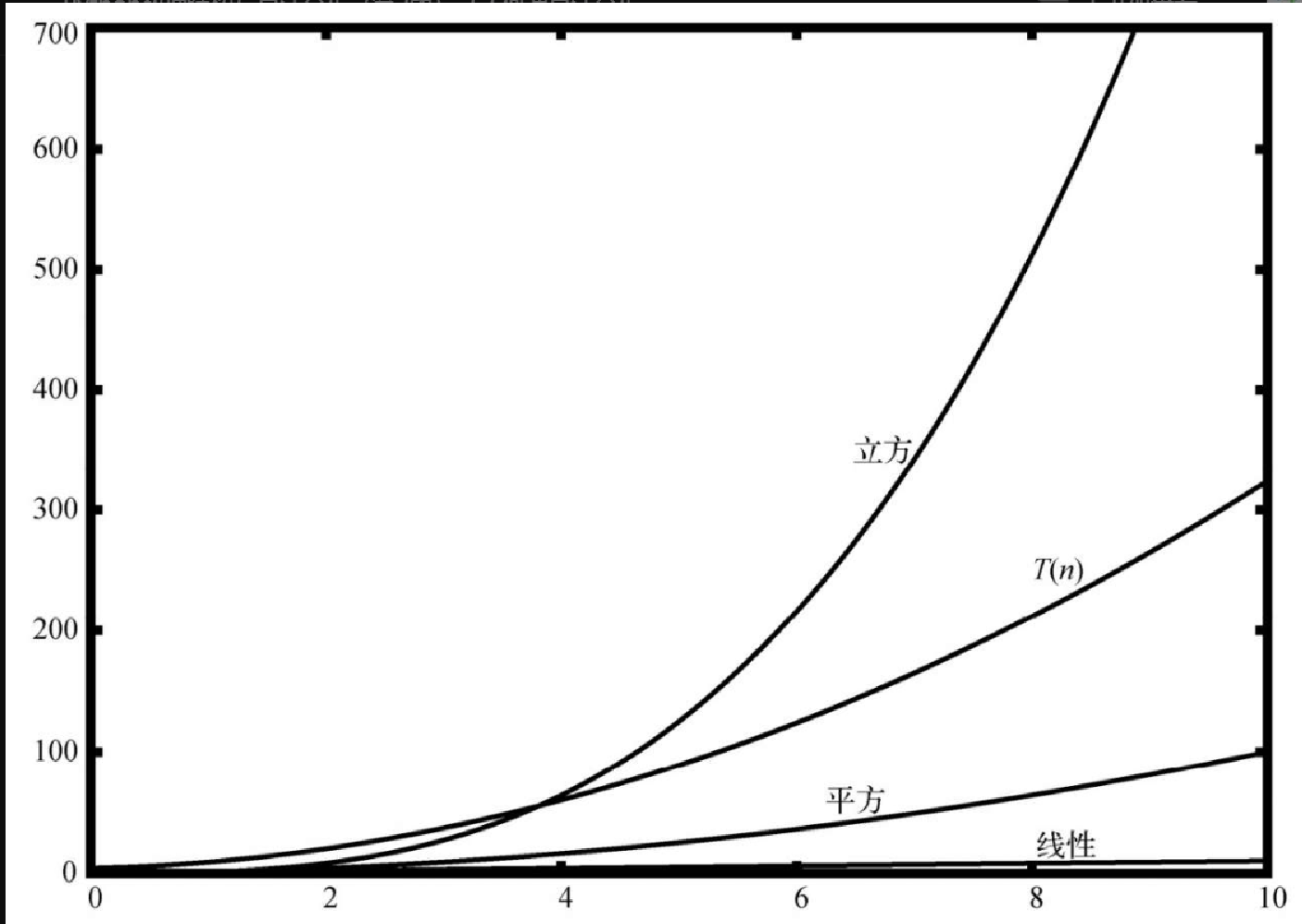
图2-2展示了一部分常见的大 \$O\$ 函数与前面讨论的 \$T(n)\$ 函数的对比情况。注意,\$T(n)\$ 一开始比立方函数大。然而,随着 n 的增长,立方函数很快就超越了 \$T(n)\$。
异序词检测示例
要展示不同数量级的算法,一个好例子就是经典的异序词检测问题。如果一个字符串只是重排了另一个字符串的字符,那么这个字符串就是另一个的异序词,比如 heart 与 earth,以及 python 与 typhon。为了简化问题,假设要检查的两个字符串长度相同,并且都是由 26 个英文字母的小写形式组成的。我们的目标是编写一个布尔函数,它接受两个字符串,并能判断它们是否为异序词。
方案1:清点法
清点第 1 个字符串的每个字符,看看它们是否都出现在第 2 个字符串中。如果是,那么两个字符串必然是异序词。清点是通过用 Python 中的特殊值 None 取代字符来实现的。但是,因为 Python 中的字符串是不可修改的,所以先要将第 2 个字符串转换成列表。在字符列表中检查第 1 个字符串中的每个字符,如果找到了,就替换掉。代码清单 2-6 给出了这个函数。
def anagramSolution1(s1,s2):
stillOK = True
if len(s1) != len(s2):
stillOK = False
alist = list(s2)
pos1 = 0
while pos1 < len(s1) and stillOK:
pos2 = 0
found = False
while pos2 < len(alist) and not found:
if s1[pos1] == alist[pos2]:
found = True
else:
pos2 = pos2 + 1
if found:
alist[pos2] = None
else:
stillOK = False
pos1 = pos1 + 1
return stillOK
print(anagramSolution1('abcd','dcba'))来分析这个算法。注意,对于 s1 中的 n 个字符,检查每一个时都要遍历 s2 中的 n 个字符。要匹配 s1 中的一个字符,列表中的 n 个位置都要被访问一次。因此,访问次数就成了从 1 到 n 的整数之和。这可以用以下公式来表示。
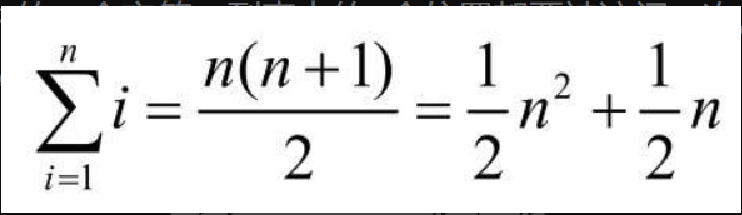
当 n 变大时,起决定性作用的是 n2,而其它可以忽略。所以,这个方案的时间复杂度是 \$O(n^2)\$。
方案2:排序法
尽管 s1 与 s2 是不同的字符串,但只要由相同的字符构成,它们就是异序词。基于这一点,可以采用另一个方案。如果按照字母表顺序给字符排序,异序词得到的结果将是同一个字符串。代码清单2-7 给出了这个方案的实现代码。在 Python 中,可以先将字符串转换为列表,然后使用内建的 sort 方法对列表排序。
def anagramSolution2(s1,s2):
alist1 = list(s1)
alist2 = list(s2)
alist1.sort()
alist2.sort()
pos = 0
matches = True
while pos < len(s1) and matches:
if alist1[pos]==alist2[pos]:
pos = pos + 1
else:
matches = False
return matches
print(anagramSolution2('abcde','edcba'))乍看之下,你可能会认为这个算法的时间复杂度是 \$O(n)\$,因为在排序之后只需要遍历一次就可以比较 n 个字符。但是,调用两次 sort 方法不是没有代价。我们在后面会看到,排序的时间复杂度基本上是 \$O(n^2)\$或 \$O(nlogn)\$,所以排序操作起主导作用。也就是说,该算法和排序过程的数量级相同。
方案3:蛮力法
用蛮力解决问题的方法基本上就是穷尽所有的可能。就异序词检测问题而言,可以用 s1 中的字符生成所有可能的字符串,看看 s2 是否在其中。但这个方法有个难处。用 s1 中的字符生成所有可能的字符串时,第 1 个字符有 n 种可能,第 2 个字符有 n-1 种可能,第 3 个字符有 n-2 种可能,依此类推。字符串的总数是 n*(n-1)*(n-2)*…*3*2*1,即 n!。也许有些字符串会重复,但程序无法预见,所以肯定会生成 n! 个字符串。
当 n 较大时,n! 增长得比 2n 还要快。实际上,如果 s1 有 20 个字符,那么字符串的个数就是 20!=2432902008176640000。假设每秒处理一个,处理完整个列表要花 77146816596 年。这可不是个好方案。
方案4:计数法
最后一个方案基于这样一个事实:两个异序词有同样数目的 a、同样数目的 b、同样数目的 c,等等。要判断两个字符串是否为异序词,先数一下每个字符出现的次数。因为字符可能有 26 种,所以使用 26 个计数器,对应每个字符。每遇到一个字符,就将对应的计数器加 1。最后,如果两个计数器列表相同,那么两个字符串肯定是异序词。代码清单2-8 给出了这个方案的实现代码。
def anagramSolution4(s1,s2):
c1 = [0]*26
c2 = [0]*26
for i in range(len(s1)):
pos = ord(s1[i])-ord('a')
c1[pos] = c1[pos] + 1
for i in range(len(s2)):
pos = ord(s2[i])-ord('a')
c2[pos] = c2[pos] + 1
j = 0
stillOK = True
while j<26 and stillOK:
if c1[j]==c2[j]:
j = j + 1
else:
stillOK = False
return stillOK
print(anagramSolution4('apple','pleap'))这个方案也有循环。但不同于方案 1,这个方案的循环没有嵌套。前两个计数循环都是 n 阶的。第 3 个循环比较两个列表,由于可能有 26 种字符,因此会循环 26 次。全部加起来,得到总步骤数 \$T(n)=2n+26\$,即 \$O(n)\$。我们找到了解决异序词检测问题的线性阶算法。
结束这个例子的讲解之前,需要聊聊空间需求。尽管方案4的执行时间是线性的,它还是要用额外的空间来存储计数器。也就是说,这个算法用空间换来了时间。
这种情形很常见。很多时候,都需要在时间和空间之间进行权衡。本例中,额外使用的空间并不大。不过,如果有数以百万计的字符,那就有问题了。面对多种算法和具体的问题,计算机科学家需要决定如何利用好计算资源。