队列

接下来学习另一个线性数据结构：队列。与栈类似，队列本身十分简单，却能用来解决众多重要问题。

何谓队列

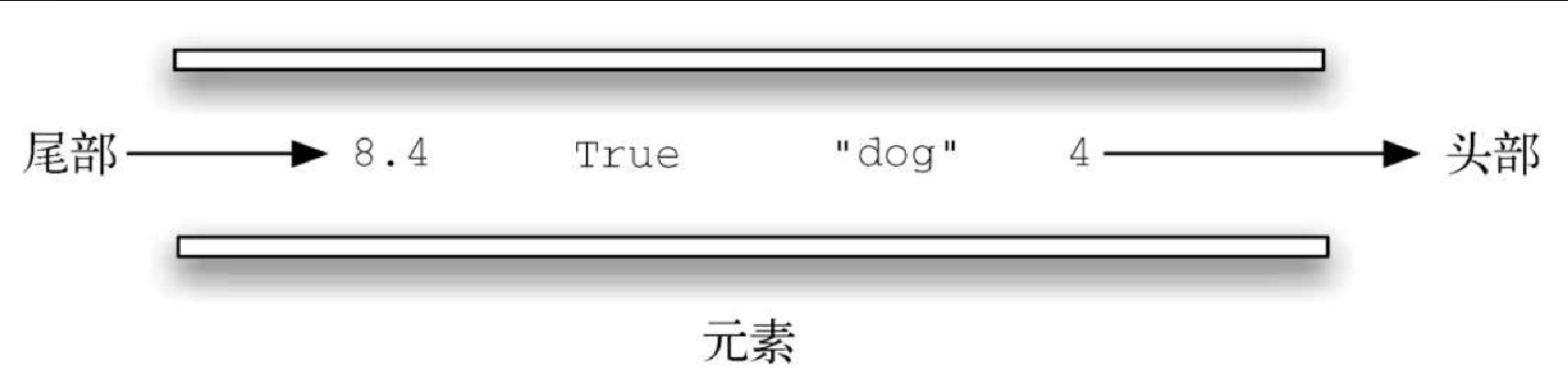
队列是有序集合，添加操作发生在 “尾部”，移除操作则发生在 “头部”。新元素从尾部进入队列，然后一直向前移动到头部，直到成为下一个被移除的元素。

最新添加的元素必须在队列的尾部等待，在队列中时间最长的元素则排在最前面。这种排序原则被称作 FIFO（first-in first-out），即先进先出，也称先到先得。

在日常生活中，我们经常排队，这便是最简单的队列例子。进电影院要排队，在超市结账要排队，买咖啡也要排队（等着从盘子栈中取盘子）。好的队列只允许一头进，另一头出，不可能发生插队或者中途离开的情况。图3-12 展示了一个由 Python 数据对象组成的简单队列。

image 2023 12 12 20 56 15 666
Figure 1. 图3-12 由Python数据对象组成的队列

计算机科学中也有众多的队列例子。我的计算机实验室有30台计算机，它们都与同一台打印机相连。当学生需要打印的时候，他们的打印任务会进入一个队列。该队列中的第一个任务就是即将执行的打印任务。如果一个任务排在队列的最后面，那么它必须等到前面的任务都执行完毕后才能执行。我们稍后会更深入地探讨这个有趣的例子。

操作系统使用一些队列来控制计算机进程。调度机制往往基于一个队列算法，其目标是尽可能快地执行程序，同时服务尽可能多的用户。在打字时，我们有时会发现字符出现的速度比击键速度慢。这是由于计算机正在做其他的工作。击键操作被放入一个类似于队列的缓冲区，以便对应的字符按正确的顺序显示。

队列抽象数据类型

队列抽象数据类型由下面的结构和操作定义。如前所述，队列是元素的有序集合，添加操作发生在其尾部，移除操作则发生在头部。队列的操作顺序是 FIFO，它支持以下操作。

  • Queue() 创建一个空队列。它不需要参数，且会返回一个空队列。

  • enqueue(item) 在队列的尾部添加一个元素。它需要一个元素作为参数，不返回任何值。

  • dequeue() 从队列的头部移除一个元素。它不需要参数，且会返回一个元素，并修改队列的内容。

  • isEmpty() 检查队列是否为空。它不需要参数，且会返回一个布尔值。

  • size() 返回队列中元素的数目。它不需要参数，且会返回一个整数。

假设 q 是一个新创建的空队列。表3-5 展示了对 q 进行一系列操作的结果。在 “队列内容” 一列中，队列的头部位于右端。4 是第一个被添加到队列中的元素，因此它也是第一个被移除的元素。

image 2023 12 12 20 58 21 104
Figure 2. 表3-5 队列操作示例

用Python实现队列

创建一个新类来实现队列抽象数据类型是十分合理的。像之前一样，我们利用简洁强大的列表来实现队列。

需要确定列表的哪一端是队列的尾部，哪一端是头部。代码清单3-9 中的实现假设队列的尾部在列表的位置 0 处。如此一来，便可以使用 insert 函数向队列的尾部添加新元素。pop 则可用于移除队列头部的元素（列表中的最后一个元素）。这意味着添加操作的时间复杂度是 \$O(n)\$，移除操作则是 \$O(1)\$。

代码清单3-9 用Python实现队列
class Queue:
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []

    def enqueue(self, item):
        self.items.insert(0,item)

    def dequeue(self):
        return self.items.pop()

    def size(self):
        return len(self.items)

以下展示了表3-5 中的队列操作及其返回结果。

>>> q = Queue()
>>> q.isEmpty()
True
>>> q.enqueue('dog')
>>> q.enqueue(4)
>>> q = Queue()
>>> q.isEmpty()
True
>>> q.enqueue(4)
>>> q.enqueue('dog')
>>> q.enqueue(True)
>>> q.size()
3
>>> q.isEmpty()
False
>>> q.enqueue(8.4)
>>> q.dequeue()
4
>>> q.dequeue()
'dog'
>>> q.size()
2

模拟：传土豆

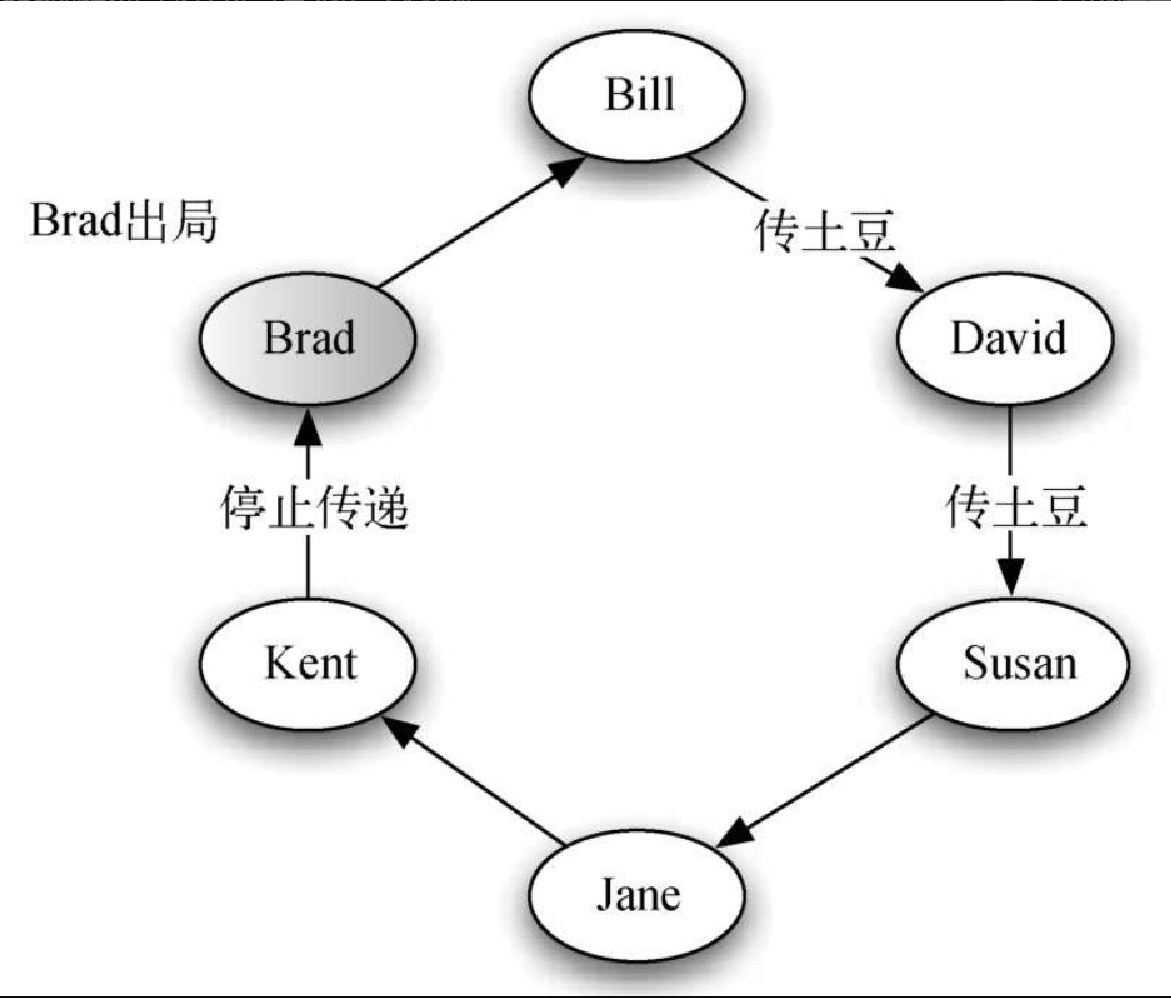
展示队列用法的一个典型方法是模拟需要以 FIFO 方式管理数据的真实场景。考虑这样一个儿童游戏：传土豆。在这个游戏中，孩子们围成一圈，并依次尽可能快地传递一个土豆，如图3-13 所示。在某个时刻，大家停止传递，此时手里有土豆的孩子就得退出游戏。重复上述过程，直到只剩下一个孩子。

image 2023 12 12 21 05 28 799
Figure 3. 图3-13 六人传土豆游戏

这个游戏其实等价于著名的约瑟夫斯问题。弗拉维奥·约瑟夫斯是公元1世纪著名的历史学家。相传，约瑟夫斯当年和39个战友在山洞中对抗罗马军队。眼看着即将失败，他们决定舍生取义。于是，他们围成一圈，从某个人开始，按顺时针方向杀掉第7人。约瑟夫斯同时也是卓有成就的数学家。据说，他立刻找到了自己应该站的位置，从而使自己活到了最后。当只剩下他时，约瑟夫斯加入了罗马军队，而不是自杀。这个故事有很多版本，有的说是每隔两个人，有的说最后一个人可以骑马逃跑。不管如何，问题都是一样的。

我们将针对传土豆游戏实现通用的模拟程序。该程序接受一个名字列表和一个用于计数的常量 num，并且返回最后一人的名字。至于这个人之后如何，就由你来决定吧。

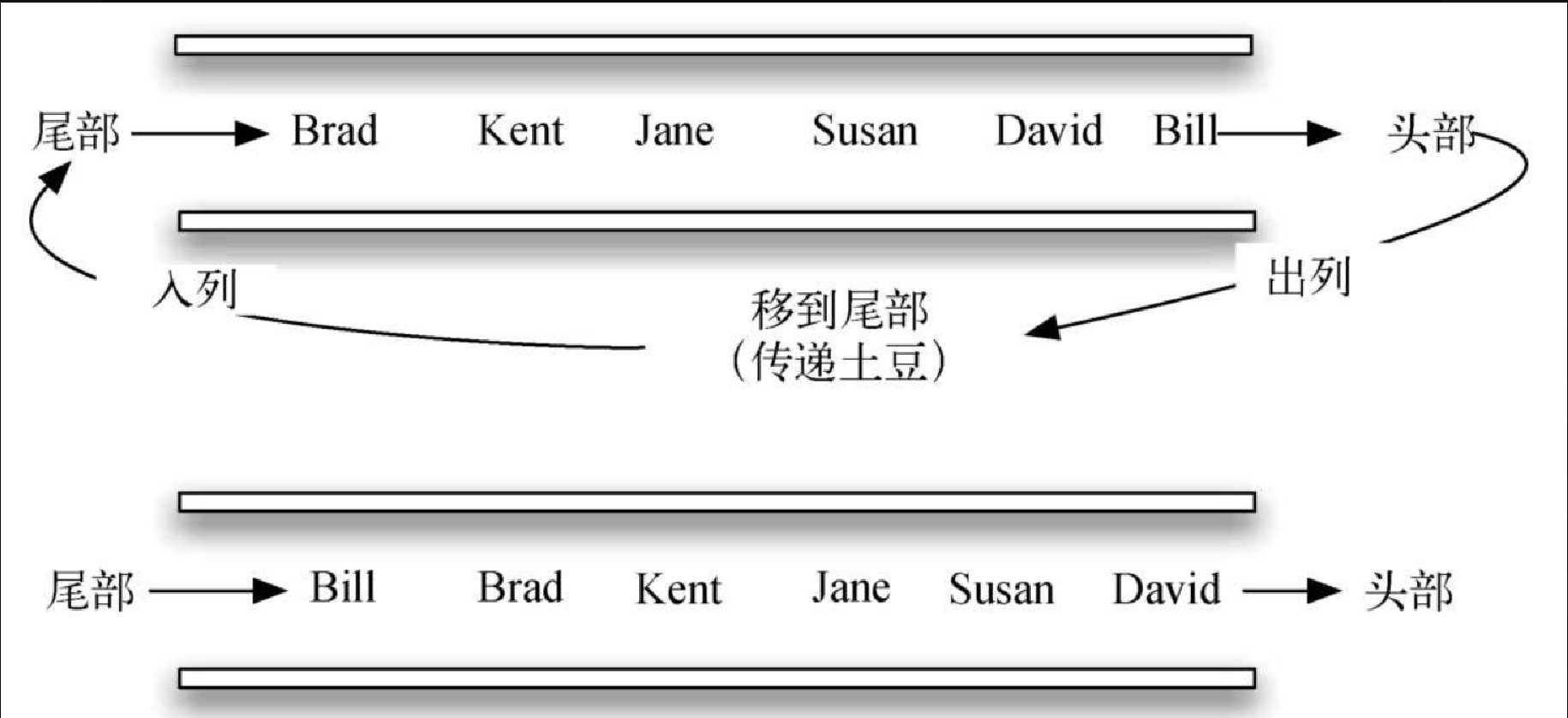
我们使用队列来模拟一个环，如图3-14 所示。假设握着土豆的孩子位于队列的头部。在模拟传土豆的过程中，程序将这个孩子的名字移出队列，然后立刻将其插入队列的尾部。随后，这个孩子会一直等待，直到再次到达队列的头部。在出列和入列 num 次之后，此时位于队列头部的孩子出局，新一轮游戏开始。如此反复，直到队列中只剩下一个名字（队列的大小为 1）。

image 2023 12 12 22 28 55 807
Figure 4. 图3-14 使用队列模拟传土豆游戏
代码清单3-10 传土豆模拟程序
from pythonds.basic import Queue

def hotPotato(namelist, num):
    simqueue = Queue()
    for name in namelist:
        simqueue.enqueue(name)

    while simqueue.size() > 1:
        for i in range(num):
            simqueue.enqueue(simqueue.dequeue())

        simqueue.dequeue()

    return simqueue.dequeue()

print(hotPotato(["Bill","David","Susan","Jane","Kent","Brad"],7))

调用 hotPotato 函数，使用 7 作为计数常量，将得到以下结果。

>>> hotPotato(["Bill", "David", "Susan", "Jane", "Kent", "Brad"], 7)
'Susan'

注意，在上例中，计数常量大于列表中的名字个数。这不会造成问题，因为队列模拟了一个环。同时需要注意，当名字列表载入队列时，列表中的第一个名字出现在队列的头部。在上例中，Bill是列表中的第一个元素，因此处在队列的最前端。在章末的编程练习中，你将修改这一实现，使程序允许随机计数

模拟：打印任务

一个更有趣的例子是模拟前文提到的打印任务队列。学生向共享打印机发送打印请求，这些打印任务被存在一个队列中，并且按照先到先得的顺序执行。这样的设定可能导致很多问题。其中最重要的是，打印机能否处理一定量的工作。如果不能，学生可能会由于等待过长时间而错过要上的课。

考虑计算机科学实验室里的这样一个场景：在任何给定的一小时内，实验室里都有约 10 个学生。他们在这一小时内最多打印 2 次，并且打印的页数从 1 到 20 不等。实验室的打印机比较老旧，每分钟只能以低质量打印 10 页。可以将打印质量调高，但是这样做会导致打印机每分钟只能打印 5 页。降低打印速度可能导致学生等待过长时间。那么，应该如何设置打印速度呢？

可以通过构建一个实验室模型来解决该问题。我们需要为学生、打印任务和打印机构建对象，如图3-15 所示。当学生提交打印任务时，我们需要将它们加入等待列表中，该列表是打印机上的打印任务队列。当打印机执行完一个任务后，它会检查该队列，看看其中是否还有需要处理的任务。我们感兴趣的是学生平均需要等待多久才能拿到打印好的文章。这个时间等于打印任务在队列中的平均等待时间。

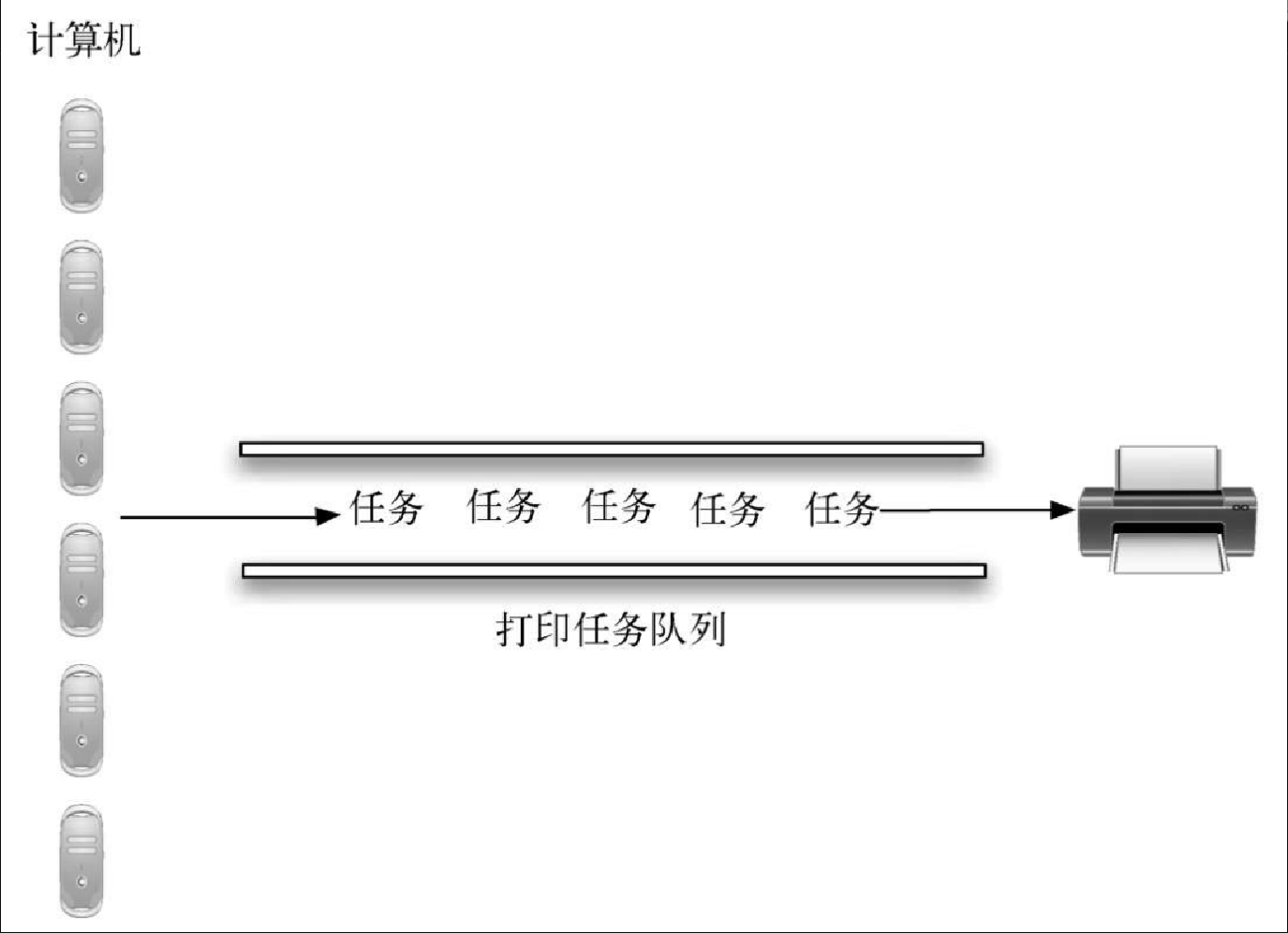
image 2023 12 12 22 32 24 395
Figure 5. 图3-15 模拟打印任务队列

在模拟时，需要应用一些概率学知识。举例来说，学生打印的文章可能有 1～20 页。如果各页数出现的概率相等，那么打印任务的实际时长可以通过 1～20 的一个随机数来模拟。

如果实验室里有 10 个学生，并且在一小时内每个人都打印两次，那么每小时平均就有 20 个打印任务。在任意一秒，创建一个打印任务的概率是多少？回答这个问题需要考虑任务与时间的比值。每小时 20 个任务相当于每 180 秒 1 个任务。

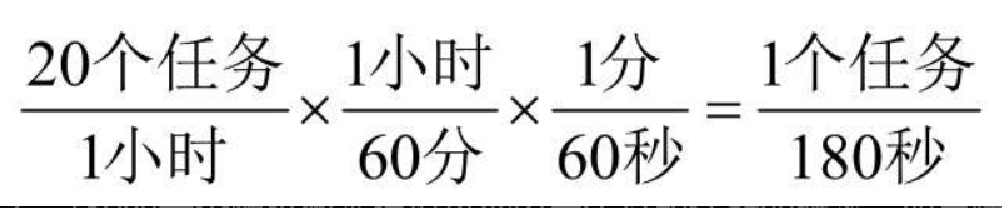
image 2023 12 12 22 33 23 949

可以通过 1～180 的一个随机数来模拟每秒内产生打印任务的概率。如果随机数正好是 180，那么就认为有一个打印任务被创建。注意，可能会出现多个任务接连被创建的情况，也可能很长一段时间内都没有任务。这就是模拟的本质。我们希望在常用参数已知的情况下尽可能准确地模拟。

  1. 主要模拟步骤

    下面是主要的模拟步骤。

    (1) 创建一个打印任务队列。每一个任务到来时都会有一个时间戳。一开始，队列是空的。

    (2) 针对每一秒（currentSecond），执行以下操作。

    • 是否有新创建的打印任务？如果是，以 currentSecond 作为其时间戳并将该任务加入到队列中。

    • 如果打印机空闲，并且有正在等待执行的任务，执行以下操作：

      • 从队列中取出第一个任务并提交给打印机；

      • 用 currentSecond 减去该任务的时间戳，以此计算其等待时间；

      • 将该任务的等待时间存入一个列表，以备后用；

      • 根据该任务的页数，计算执行时间。

    • 打印机进行一秒的打印，同时从该任务的执行时间中减去一秒。

    • 如果打印任务执行完毕，或者说任务需要的时间减为 0，则说明打印机回到空闲状态。

    (3) 当模拟完成之后，根据等待时间列表中的值计算平均等待时间。

  2. Python实现

    我们创建 3 个类：Printer、Task 和 PrintQueue。它们分别模拟打印机、打印任务和队列。Printer 类（代码清单3-11）需要检查当前是否有待完成的任务。如果有，那么打印机就处于工作状态（第13～17行），并且其工作所需的时间可以通过要打印的页数来计算。其构造方法会初始化打印速度，即每分钟打印多少页。tick 方法会减量计时，并且在执行完任务之后将打印机设置成空闲状态（第 11 行）。

    class Printer:
    def __init__(self, ppm):
        self.pagerate = ppm
        self.currentTask = None
        self.timeRemaining = 0

    def tick(self):
        if self.currentTask != None:
            self.timeRemaining = self.timeRemaining - 1
            if self.timeRemaining <= 0:
                self.currentTask = None

    def busy(self):
        if self.currentTask != None:
            return True
        else:
            return False

    def startNext(self,newtask):
        self.currentTask = newtask
        self.timeRemaining = newtask.getPages() * 60/self.pagerate

    Task 类（代码清单 3-12）代表单个打印任务。当任务被创建时，随机数生成器会随机提供页数，取值范围是 1～20。我们使用 random 模块中的 randrange 函数来生成随机数。

    >>> import random
>>> random.randrange(1, 21)
18
>>> random.randrange(1, 21)
8
    代码清单3-12 Task类
    import random

class Task:
    def __init__(self,time):
        self.timestamp = time
        self.pages = random.randrange(1,21)

    def getStamp(self):
        return self.timestamp

    def getPages(self):
        return self.pages

    def waitTime(self, currenttime):
        return currenttime - self.timestamp

    每一个任务都需要保存一个时间戳，用于计算等待时间。这个时间戳代表任务被创建并放入打印任务队列的时间。waitTime 方法可以获得任务在队列中等待的时间。

    主模拟程序（代码清单 3-13）实现了之前描述的算法。printQueue 对象是队列抽象数据类型的实例。布尔辅助函数 newPrintTask 判断是否有新创建的打印任务。我们再一次使用 random 模块中的 randrange 函数来生成随机数，不过这一次的取值范围是 1～180。平均每 180 秒有一个打印任务。通过从随机数中选取 180（第 34 行），可以模拟这个随机事件。该模拟程序允许设置总时间和打印机每分钟打印多少页。

    代码清单3-13 打印任务模拟程序
    from pythonds.basic.queue Queue

import random

def simulation(numSeconds, pagesPerMinute):

    labprinter = Printer(pagesPerMinute)
    printQueue = Queue()
    waitingtimes = []

    for currentSecond in range(numSeconds):

      if newPrintTask():
         task = Task(currentSecond)
         printQueue.enqueue(task)

      if (not labprinter.busy()) and (not printQueue.isEmpty()):
        nexttask = printQueue.dequeue()
        waitingtimes.append(nexttask.waitTime(currentSecond))
        labprinter.startNext(nexttask)

      labprinter.tick()

    averageWait=sum(waitingtimes)/len(waitingtimes)
    print("Average Wait %6.2f secs %3d tasks remaining."%(averageWait,printQueue.size()))

def newPrintTask():
    num = random.randrange(1,181)
    if num == 180:
        return True
    else:
        return False

for i in range(10):
    simulation(3600,5)

    每次模拟的结果不一定相同。对此，我们不需要在意。这是由于随机数的本质导致的。我们感兴趣的是当参数改变时结果出现的趋势。下面是一些结果。

    >>>for i in range(10):
      simulation(3600, 5)


Average Wait 165.38 secs 2 tasks remaining.
Average Wait   95.07 secs 1 tasks remaining.
Average Wait   65.05 secs 2 tasks remaining.
Average Wait   99.74 secs 1 tasks remaining.
Average Wait   17.27 secs 0 tasks remaining.
Average Wait 239.61 secs 5 tasks remaining.
Average Wait   75.11 secs 1 tasks remaining.
Average Wait   48.33 secs 0 tasks remaining.
Average Wait   39.31 secs 3 tasks remaining.
Average Wait 376.05 secs 1 tasks remaining.

    首先，模拟 60 分钟（3600 秒）内打印速度为每分钟 5 页。并且，我们进行 10 次这样的模拟。由于模拟中使用了随机数，因此每次返回的结果都不同。

    在模拟 10 次之后，可以看到平均等待时间是 122.092 秒，并且等待时间的差异较大，从最短的 17.27 秒到最长的 376.05 秒。此外，只有 2 次在给定时间内完成了所有任务。

    现在把打印速度改成每分钟 10 页，然后再模拟 10 次。由于加快了打印速度，因此我们希望一小时内能完成更多打印任务。

    >>>for i in range(10):
      simulation(3600, 10)


Average Wait    1.29 secs 0 tasks remaining.
Average Wait    7.00 secs 0 tasks remaining.
Average Wait   28.96 secs 1 tasks remaining.
Average Wait   13.55 secs 0 tasks remaining.
Average Wait   12.67 secs 0 tasks remaining.
Average Wait    6.46 secs 0 tasks remaining.
Average Wait   22.33 secs 0 tasks remaining.
Average Wait   12.39 secs 0 tasks remaining.
Average Wait    7.27 secs 0 tasks remaining.
Average Wait   18.17 secs 0 tasks remaining.
    from pythonds.basic import Queue

import random

class Printer:
    def __init__(self, ppm):
        self.pagerate = ppm
        self.currentTask = None
        self.timeRemaining = 0

    def tick(self):
        if self.currentTask != None:
            self.timeRemaining = self.timeRemaining - 1
            if self.timeRemaining <= 0:
                self.currentTask = None

    def busy(self):
        if self.currentTask != None:
            return True
        else:
            return False

    def startNext(self,newtask):
        self.currentTask = newtask
        self.timeRemaining = newtask.getPages() * 60/self.pagerate

class Task:
    def __init__(self,time):
        self.timestamp = time
        self.pages = random.randrange(1,21)

    def getStamp(self):
        return self.timestamp

    def getPages(self):
        return self.pages

    def waitTime(self, currenttime):
        return currenttime - self.timestamp


def simulation(numSeconds, pagesPerMinute):

    labprinter = Printer(pagesPerMinute)
    printQueue = Queue()
    waitingtimes = []

    for currentSecond in range(numSeconds):

      if newPrintTask():
         task = Task(currentSecond)
         printQueue.enqueue(task)

      if (not labprinter.busy()) and (not printQueue.isEmpty()):
        nexttask = printQueue.dequeue()
        waitingtimes.append( nexttask.waitTime(currentSecond))
        labprinter.startNext(nexttask)

      labprinter.tick()

    averageWait=sum(waitingtimes)/len(waitingtimes)
    print("Average Wait %6.2f secs %3d tasks remaining."%(averageWait,printQueue.size()))

def newPrintTask():
    num = random.randrange(1,181)
    if num == 180:
        return True
    else:
        return False

for i in range(10):
    simulation(3600,5)

  3. 讨论

    在之前的内容中，我们试图解答这样一个问题：如果提高打印质量并降低打印速度，打印机能否及时完成所有任务？我们编写了一个程序来模拟随机提交的打印任务，待打印的页数也是随机的。

    上面的输出结果显示，按每分钟 5 页的打印速度，任务的等待时间在 17.27 秒和 376.05 秒之间，相差约 6 分钟。提高打印速度之后，等待时间在 1.29 秒和 28.96 秒之间。此外，在每分钟 5 页的速度下，10 次模拟中有 8 次没有按时完成所有任务。

    可见，降低打印速度以提高打印质量，并不是明智的做法。学生不能等待太长时间，当他们要赶去上课时尤其如此。6分钟的等待时间实在是太长了。

    这种模拟分析能帮助我们回答很多 “如果” 问题。只需改变参数，就可以模拟感兴趣的任意行为。以下是几个例子。

    • 如果实验室里的学生增加到 20 个，会怎么样？

    • 如果是周六，学生不需要上课，他们是否愿意等待？

    • 如果每个任务的页数变少了，会怎么样？（因为 Python 既强大又简洁，所以学生不必写太多行代码。）

    这些问题都能通过修改本例中的模拟程序来解答。但是，模拟的准确度取决于它所基于的假设和参数。真实的打印任务数量和学生数目是准确构建模拟程序必不可缺的数据。