复习图:模式匹配

尽管计算机图形学越来越受重视，但是文字信息处理依然是重要的研究领域，特别是在长字符串中寻找模式。这种模式常被称作子串。为了找到模式，会进行某种搜索，至少要能找到模式首次出现的位置。我们也可以想想这个问题的扩展版本，即如何找到模式出现的所有位置。

Python 有一个内置的 find 方法，可用于在给定字符串的情况下返回模式首次出现的位置，如下所示。

>>> "ccabababcab".find("ab")
2
>>> "ccabababcab".find("xyz")
-1

子串 ab 第一次出现在字符串 ccabababcab 的位置 2 处。如果模式没有出现，会返回 -1。

生物学字符串

生物信息学领域正在孕育一些激动人心的算法，特别是如何管理和处理大量的生物数据。这些数据中有很多是以编码遗传物质的形式存储于染色体中的。脱氧核糖核酸（以下简称 DNA）为蛋白质合成提供了蓝图。

DNA 基本上是由 4 种碱基构成的长序列，这 4 种碱基分别是腺嘌呤（A）、胸腺嘧啶（T）、鸟嘌呤（G）和胞嘧啶（C）。以上 4 个字母常被称作 “基因字母表”，一段 DNA 就表示为由这 4 个字母组成的序列。比如，DNA 串 ATCGTAGAGTCAGTAGAGACTADTGGTACGA 编码了 DNA 的一小部分。这些长长的字符串可能包含数以百万计的 “基因字母”，其中某些小段为基因编码提供了丰富的信息。可见，对于生物信息学研究人员来说，掌握找到这些小段的方法非常重要。

现在，问题得以简化：给定一个由 A、T、G、C 组成的字符串，开发出能定位某个特定模式的算法。我们常常称 DNA 串为 “文本”。如果模式不存在，我们也希望能通过算法知道。此外，由于这些字符串往往很长，因此需要保证算法的效率。

简单比较

要解决 DNA 串的模式匹配问题，你可能立刻会想到直接尝试匹配模式和文本的所有可能。图8-21 展示了这一算法的原理。我们从左往右，挨个比较文本和模式的字母。如果当前字母匹配，就比较下一个。如果字母不匹配，将模式往右滑动一个位置，重新开始比较。

Figure 1. 图8-21 简单的模式匹配算法

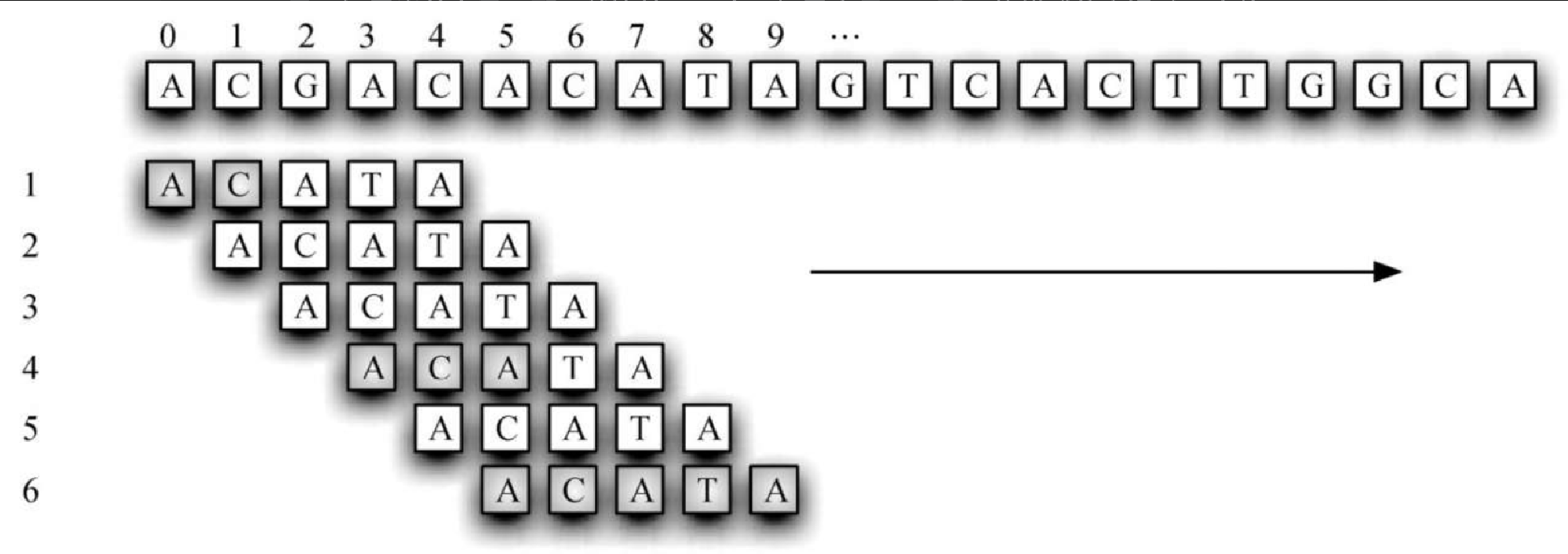
本例中，我们在第 6 次尝试时发现字母匹配，此时位于位置 5 处。带阴影的字母表示在移动模式的过程中有部分字母匹配。代码清单8-28 给出了这种算法的 Python 实现。以模式和文本为参数，如果发现模式匹配，就返回子串在文本中的起始位置；如果匹配失败，则返回 -1。

代码清单8-28 简单的模式匹配器

def simpleMatcher(pattern, text):
    starti = 0  # 记录每次尝试的起点
    i = 0  # 文本的下标
    j = 0  # 模式的下标
    match = False
    stop = False
    while not match and not stop:
        if text[i] == pattern[j]:
            i = i + 1
            j = j + 1
        else:
            starti = starti + 1  # 向右移动
            i = starti
            j = 0

        if j == len(pattern):
            match = True
        else:
            if i == len(text):
                stop = True

    if match:
        return i - j
    else:
        return -1

变量 i 和 j 分别作为文本和模式的下标。starti 记录每次匹配尝试的起始位置。两个布尔型变量控制匹配终止的两个条件。穷尽文本而不得时，设 stop 为 True。匹配成功时，设 match 为 True。

第 8 行检查文本中当前的字母是否与模式中当前的字母匹配。如果匹配，两个下标都递增；如果不匹配，则移动到文本中下一个位置，将模式重置到起始位置（第 13 行）。第 16 行检查是否已经处理完模式中的所有字母。如果是，就说明匹配成功；如果不是，需要检查文本中是否还有字母（第 19 行）。

假设文本长度为 n，模式长度为 m。很容易看出，这个算法的时间复杂度是 \$O(nm)\$。对于 n 个字母中的每一个，都可能需要比较模式中的全部字母（ m 个）。如果 n 和 m 比较小，这个算法的效率尚可，但是考虑到文本中有数以千计——甚至数以百万计——的字母，并且要找到更大的模式，寻找更好的算法就显得很有必要。

使用图：DFA

如果对模式做一些预处理，就可以创建时间复杂度为 \$O(n)\$ 的模式匹配器。一种做法是用图来表示模式，从而构建确定有限状态自动机，或称 DFA。在 DFA 图中，每个顶点是一个状态，用于记录匹配成功的模式数。图中每一条边代表处理文本中的一个字母后发生的转变。

图8-22 展示了前一节中的示例模式（ACATA）的 DFA。第一个顶点（状态 0）是起始状态（或称初始状态），表示还没有发现任何匹配的字母。显然，在处理文本中的第一个字母之前，就是这个状态。

Figure 2. 图8-22 确定有限状态自动机

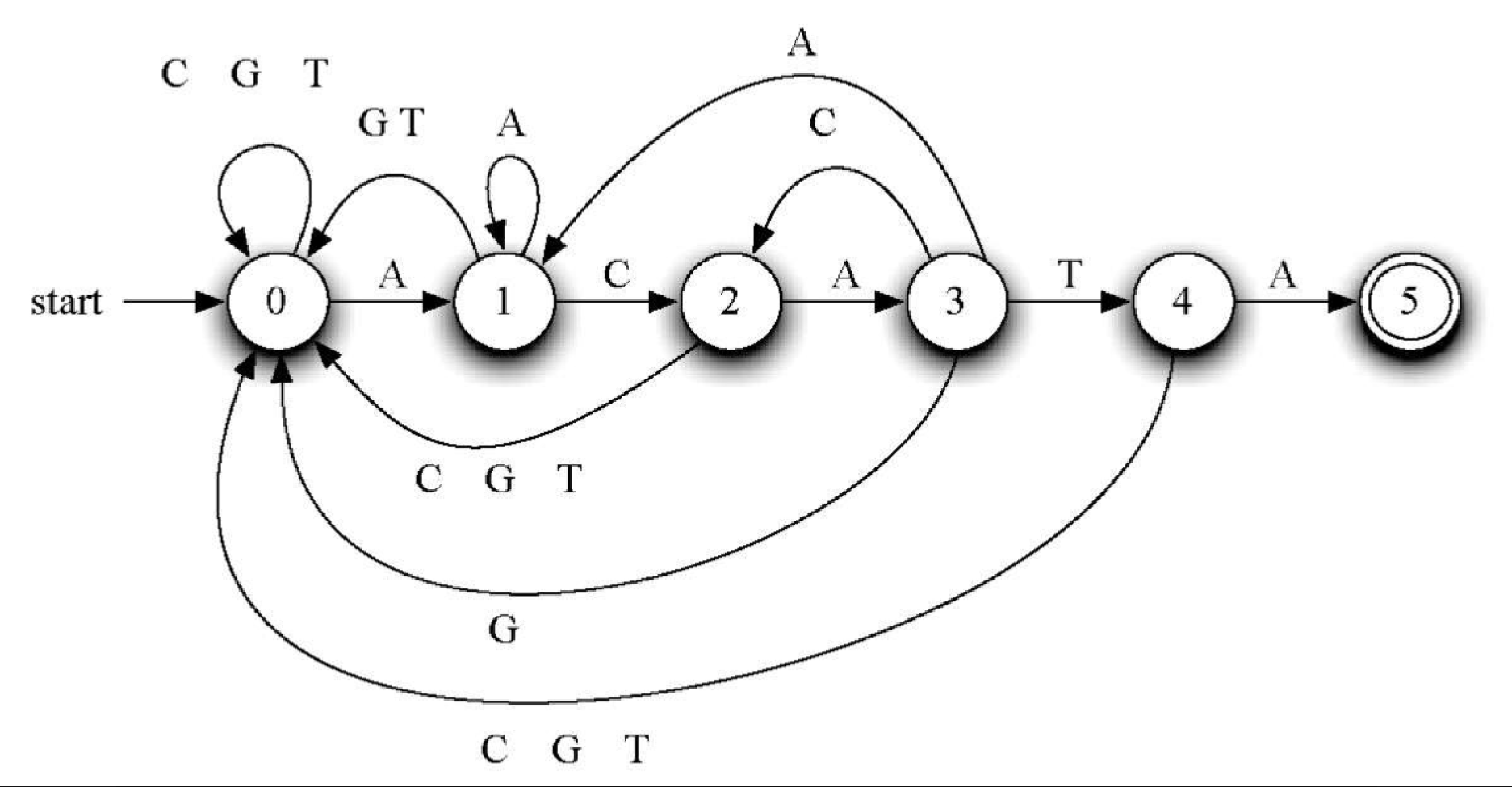
DFA 的原理很简单。记录当前状态，并在一开始时将其设为 0。读入文本中的下一个字母。根据这个字母，相应地转变为下一个状态，并将它作为新的当前状态。由定义可知，对于每个字母，每个状态有且只有一种转变。这意味着对于基因字母表，每个状态可能有4种转变。在图8-22 中，我们在某些边上标出了多个字母，这是为了表示到同一个状态的多种转变。

重复上述做法，直到终止。如果进入最终状态（DFA 图用两个同心圆表示最终状态，本例中为状态 5），就可以停下来，并报告匹配成功。也就是说，DFA 图发现了模式的一次出现。你可能注意到，最终状态不能转变为其他状态，也即必须在此停下来。模式的出现位置可以根据当前字母的位置与模式的长度计算出来。另一方面，如果当穷尽文本中的字母时处于非最终状态，我们就知道模式没有出现。

图8-23 逐步展示了在文本字符串 ACGACACATA 中寻找子串 ACATA 的过程。DFA 计算出的下一个状态就是下一步的当前状态。对于由当前状态和当前字母组成的每个组合，下一个状态都是唯一的，因此这个 DFA 图并不复杂。

Figure 3. 图8-23 逐步分析DFA模式匹配器

因为文本中的每个字母都作为 DFA 图的输入被使用一次，所以这种算法的时间复杂度是 \$O(n)\$。不过，还需要考虑构建 DFA 的预处理步骤。有很多知名算法可以根据模式生成 DFA 图。不幸的是，它们都很复杂，因为每个状态（顶点）针对每个字母都必须有一种转变（边）。那么问题就来了，是否有类似的模式匹配器，但它的边集合更简单？

使用图：KMP

前两节中的模式匹配器将文本中的每个可能匹配成功的子串都与模式比较。这样做往往是在浪费时间，因为匹配的实际起点远在之后。一种改善措施是，如果不匹配，就以多于一个字母的幅度滑动模式。图8-24 展示了这种策略，将模式滑到前一次发生不匹配的位置。

Figure 4. 图8-24 滑动幅度更大的模式匹配器

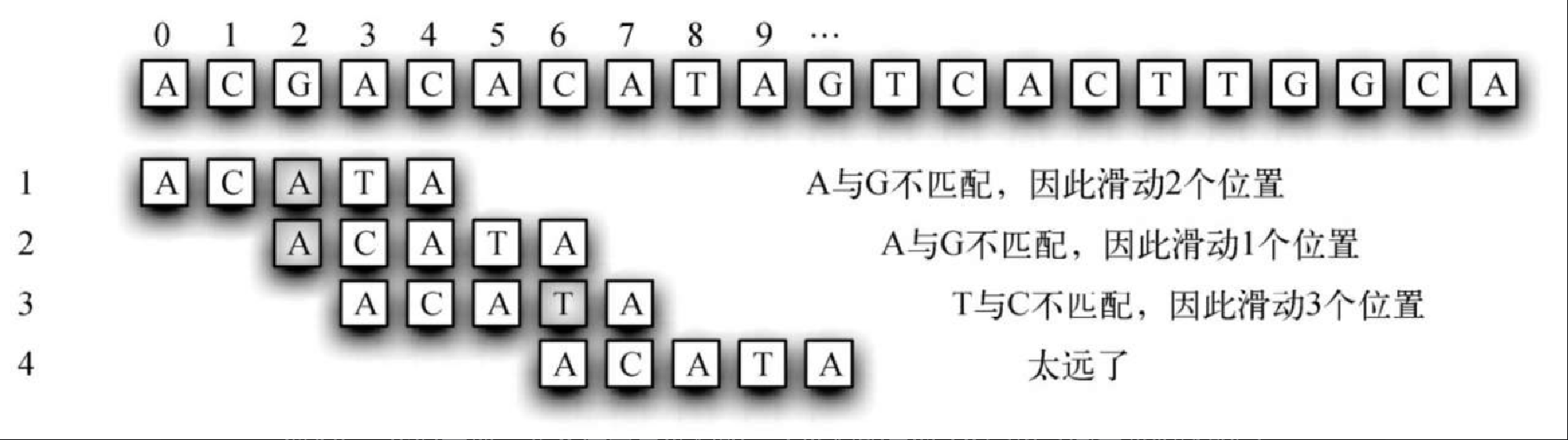
第 1 步，我们发现前两个位置是匹配的。不匹配的是第 3 个字母（图中带阴影的字母），将整个模式滑过来，下一次尝试从这一点开始。第 2 步，一上来就不匹配，没有其他选择，只能滑动到下一个位置。此时，我们发现前 3 个字母是匹配的。但有个问题：不匹配时，算法根据策略把模式滑到某个位置；但这样做就滑过头了，也就是漏掉了模式在文本串中真正的起点（位置 5）。

这个方案失败的原因在于，没有利用前一次不匹配时模式和文本的内容信息。在第 2 步中，文本串的最后 2 个字母（位置 5 和位置 6）实际上是和模式的前 2 个字母匹配的。我们称这种情况为模式的两字母前缀与文本串的两字母后缀匹配。这条信息很有价值。如果记录下前缀和后缀的重叠情况，就可以直接将模式滑动到正确位置。

基于上述思路，可以构建名为 KMP（Knuth-Morris-Pratt）的模式匹配器，它以提出这一算法的 3 位计算机科学家的姓氏命名。KMP 算法的思想就是构建图，在字母不匹配时可以提供关于 “滑动” 距离的必要信息。KMP 图也由状态（顶点）和转变（边）构成。但不同于 DFA 图，KMP 图的每个顶点只有 2 条向外的边。

图8-25 是示例模式的 KMP 图，其中有两个特殊的状态。初始状态（标有 get 的顶点）负责从输入文本中读入下一个字母。随后的转变（标有星号的边）是肯定发生的。注意，一开始从文本读入前两个字母，然后立即转到下一个状态（状态 1）。最终状态（状态 6，标有 F 的顶点）表示匹配成功，它对于图来说是终点。

Figure 5. 图8-25 KMP图示例

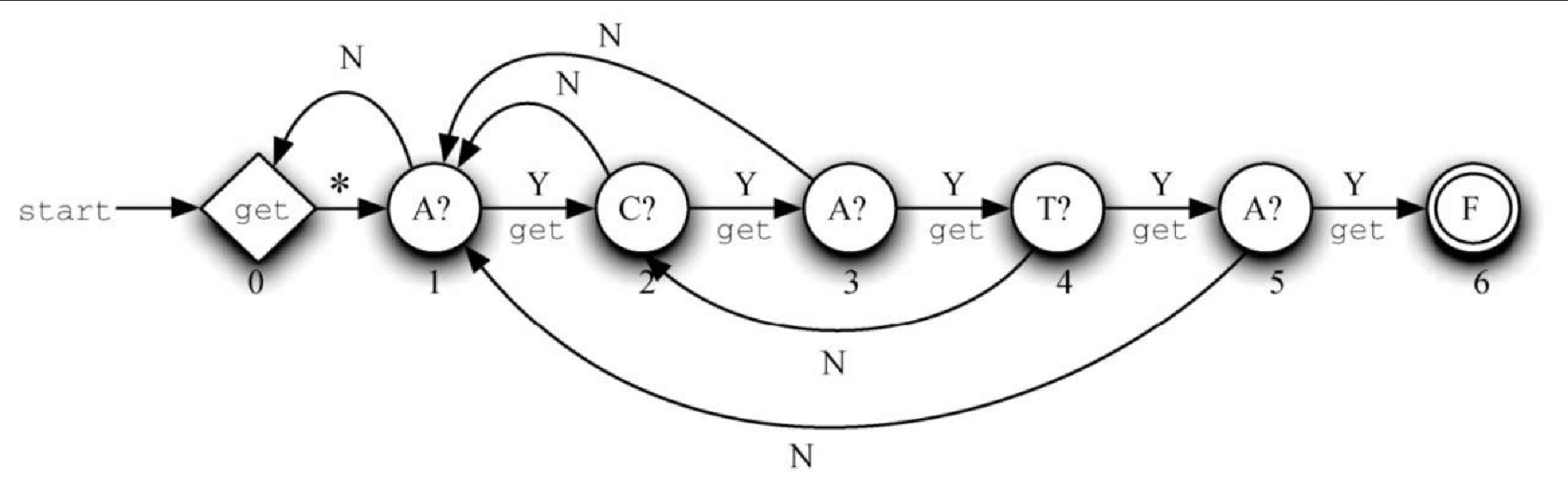
其他顶点负责比较模式中的每个字母与文本中当前的字母。例如，标有 C？的顶点检查文本中当前的字母是否为 C。如果是，就选择标有 Y 的边（Y 代表 yes，说明匹配成功），同时读入下一个字母。无论是否匹配成功，都会从文本中读入下一个字母。

标有 N 的边表示不匹配。前面解释过，遇到这种情况时，要知道滑动多少个位置。本质上，我们是要记录文本中当前的字母，并且往回移动到模式中的前一个点。为了计算，我们采用一个简单的算法（如代码清单8-29 所示），比较模式与其自身，找出前缀和后缀的重叠部分。由重叠部分的长度可知要往后挪多远。注意，使用不匹配链接时，不处理新的字母。

代码清单8-29 mismatchLinks方法

def mismatchLinks(pattern):
    augPattern = "0" + pattern
    links = {}
    links[1] = 0
    for k in range(2, len(augPattern)):
        s = links[k - 1]
        stop = False
        while s >= 1 and not stop:
            if augPattern[s] == augPattern[k - 1]:
                stop = True
            else:
                s = links[s]
        links[k] = s + 1
    return links

来看通过 mismatchLinks 方法处理模式的例子。

>>> mismatchLinks("ACATA")
{1: 0, 2: 1, 3: 1, 4: 2, 5: 1}
>>>

这个方法会返回一个字典，其中的键是当前的顶点（状态），值是不匹配链接的终点。可以看出，从 1 到 5 的每个状态分别对应模式中的每个字母，并且每个状态都有回到之前某个状态的一条边。

前面提过，不匹配链接可以通过滑动模式并寻找最长的匹配前缀和匹配后缀得到。这个方法先扩展模式，让模式中的下标对得上 KMP 图中的顶点标签。既然初始状态是状态 0，就将 0 作为扩展位上的占位符。这样一来，模式中的第 1～m 个字母就分别对应 KMP 图中的第 1～m 个状态。

第 5 行创建字典的第一项，这一项总是从顶点 1 回到初始状态的一条边，从文本串中自动读入一个新字母。之后的循环一步步扩大模式的检查范围，寻找前缀和后缀的重叠部分。如果有重叠，其长度可以用来设置下一个链接。

图8-26 逐步展示了在文本字符串 ACGACACATA 中寻找示例模式的过程。再次注意，只有在使用匹配链接后，当前字母才会变化。不匹配时，当前字母不变，比如第 4 步和第 5 步。第 6 步转变回状态 0，读入下一个字母，返回状态 1。

Figure 6. 图8-26 逐步分析KMP模式匹配器

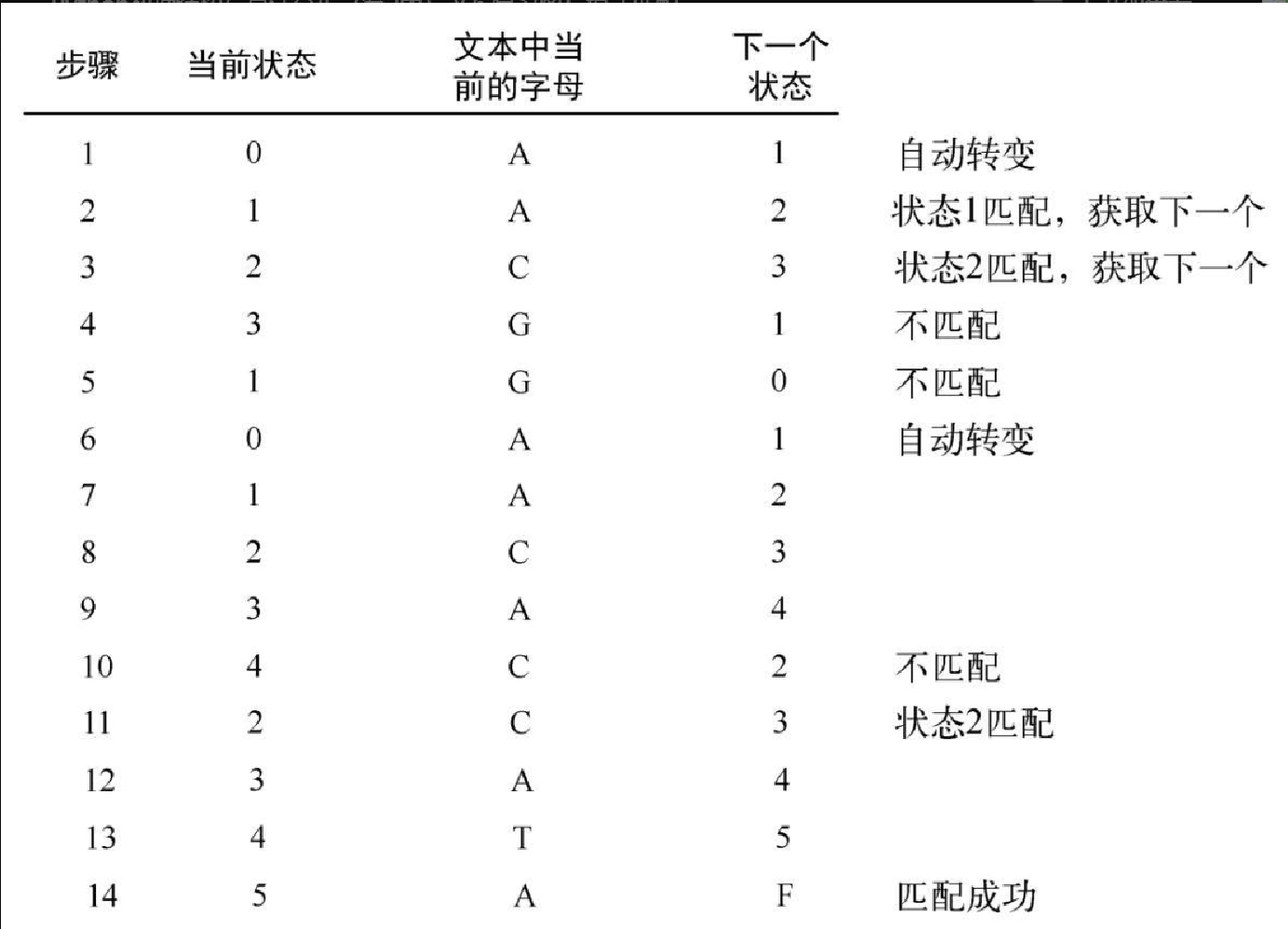
第 10 步和第 11 步体现了不匹配链接的重要性。第 10 步中当前的字母是 C，它与状态 4 需要匹配的字母不符，因此结果是一个不匹配链接。不过，既然此时发现部分字母匹配，那么这个不匹配链接就回到了正确匹配的状态 2。正因为如此，最终才匹配成功。

和 DFA 算法一样，KMP 算法的时间复杂度也是 \$O(n)\$，因为要处理文本字符串中的每个字母。不过，KMP 图构建起来要容易得多，而且所需的存储空间也少，每个顶点只有 2 条向外的边。