何谓递归
递归是解决问题的一种方法,它将问题不断地分成更小的子问题,直到子问题可以用普通的方法解决。通常情况下,递归会使用一个不停调用自己的函数。尽管表面上看起来很普通,但是递归可以帮助我们写出非常优雅的解决方案。对于某些问题,如果不用递归,就很难解决。
计算一列数之和
我们从一个简单的问题开始学习递归。即使不用递归,我们也知道如何解决这个问题。假设需要计算数字列表 [1, 3, 5, 7, 9] 的和。代码清单4-1 展示了如何通过循环函数来计算结果。这个函数使用初始值为 0 的累加变量 theSum,通过把列表中的数加到该变量中来计算所有数的和。
def listsum(numList):
theSum = 0
for i in numList:
theSum = theSum + i
return theSum
print(listsum([1,3,5,7,9]))假设暂时没有 while 循环和 for 循环。应该如何计算结果呢?如果你是数学家,就会记得加法是接受两个参数(一对数)的函数。将问题从求一列数之和重新定义成求数字对之和,可以将数字列表重写成完全括号表达式,例如 。注意,最内层的括号对 (7 + 9) 不用循环或者其他特殊语法结构就能直接求解。事实上,可以使用下面的简化步骤来求总和。
总和 = (1 + (3 + (5 + (7 + 9))))
总和 = (1 + (3 + (5 + 16)))
总和 = (1 + (3 + 21))
总和 = (1 + 24)
总和 = 25如何将上述想法转换成 Python 程序呢?让我们用 Python 列表来重新表述求和问题。数字列表 numList 的总和等于列表中的第一个元素(numList[0])加上其余元素(numList[1:])之和。可以用函数的形式来表述这个定义。
listSum(numList) = first(numList) + listSum(rest(numList))first(numList) 返回列表中的第一个元素,rest(numList) 则返回其余元素。用 Python 可以轻松地实现这个等式,如代码清单4-2 所示。
def listsum(numList):
if len(numList) == 1:
return numList[0]
else:
return numList[0] + listsum(numList[1:])
print(listsum([1,3,5,7,9]))在这一段代码中,有两个重要的思想值得探讨。首先,第 2 行检查列表是否只包含一个元素。这个检查非常重要,同时也是该函数的退出语句。对于长度为 1 的列表,其元素之和就是列表中的数。其次,listsum 函数在第 5 行调用了自己!这就是我们将 listsum 称为递归函数的原因——递归函数会调用自己。
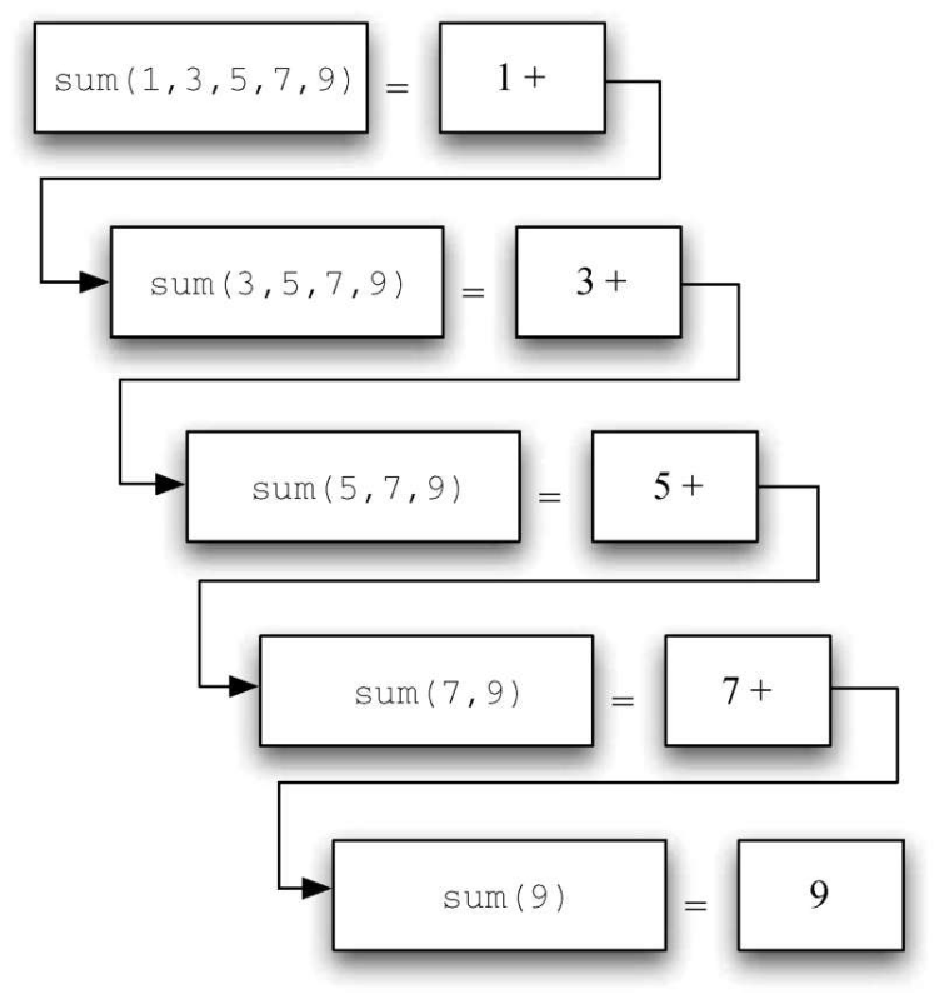
图4-1 展示了在求解 [1, 3, 5, 7, 9] 之和时的一系列递归调用。我们需要将这一系列调用看作一系列简化操作。每一次递归调用都是在解决一个更小的问题,如此进行下去,直到问题本身不能再简化为止。
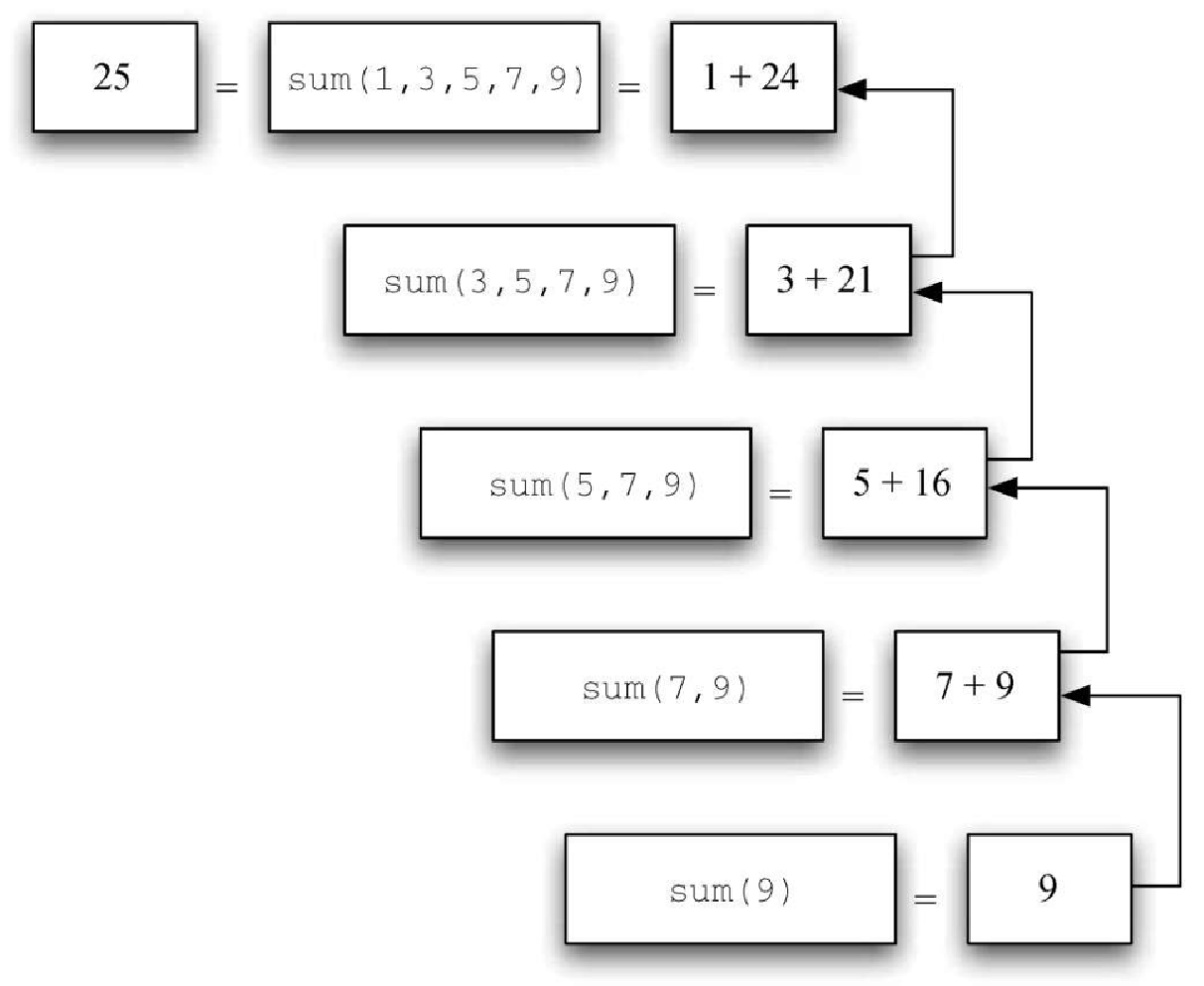
当问题无法再简化时,我们开始拼接所有子问题的答案,以此解决最初的问题。图4-2 展示了 listsum 函数在返回一系列调用的结果时进行的加法操作。当它返回到顶层时,就有了最终答案。
递归三原则
正如阿西莫夫提出的机器人三原则一样,所有的递归算法都要遵守三个重要的原则:
-
递归算法必须有基本情况;
-
递归算法必须改变其状态并向基本情况靠近;
-
递归算法必须递归地调用自己。
让我们来看看listsum算法是如何遵守上述原则的。基本情况是指使算法停止递归的条件,这通常是小到足以直接解决的问题。listsum算法的基本情况就是列表的长度为1。为了遵守第二条原则,必须设法改变算法的状态,从而使其向基本情况靠近。改变状态是指修改算法所用的某些数据,这通常意味着代表问题的数据以某种方式变得更小。listsum算法的主数据结构是一个列表,因此必须改变该列表的状态。由于基本情况是列表的长度为1,因此向基本情况靠近的做法自然就是缩短列表。这正是代码清单4-2的第5行所做的,即在一个更短的列表上调用listsum。最后一条原则是递归算法必须对自身进行调用,这正是递归的定义。对于很多新手程序员来说,递归是令他们颇感困惑的概念。新手程序员知道如何将一个大问题分解成众多小问题,并通过编写函数来解决每一个小问题。然而,递归似乎让他们落入怪圈:有一个需要用函数来解决的问题,但是这个函数通过调用自己来解决问题。其实,递归的逻辑并不是循环,而是将问题分解成更小、更容易解决的子问题。
接下来,我们会讨论更多的递归例子。在每一个例子中,我们都会根据递归三原则来构建问题的解决方案。
将整数转换成任意进制的字符串
假设需要将一个整数转换成以 2~16 为基数的字符串。例如,将 10 转换成十进制字符串 "10",或者二进制字符串 "1010"。尽管很多算法都能解决这个问题,包括 3.3.6 节讨论的算法,但是递归的方式非常巧妙。
以十进制整数 769 为例。假设有一个字符序列对应前 10 个数,比如 convString ="0123456789"。若要将一个小于 10 的数字转换成其对应的字符串,只需在字符序列中查找对应的数字即可。例如,9 对应的字符串是 convString[9] 或者 "9"。如果可以将整数 769 拆分成 7、6 和 9,那么将其转换成字符串就十分简单。因此,一个很好的基本情况就是数字小于 10。
上述基本情况说明,整个算法包含三个组成部分:
-
将原来的整数分成一系列仅有单数位的数;
-
通过查表将单数位的数转换成字符串;
-
连接得到的字符串,从而形成结果。
接下来需要设法改变状态并且逐渐向基本情况靠近。思考哪些数学运算可以缩减整数,最有可能的是除法和减法。虽然减法可能有效,但是我们并不清楚应该减去什么数。让我们来看看将需要转换的数字除以对应的进制基数会如何。
将 769 除以 10,商是 76,余数是 9。这样一来,我们便得到两个很好的结果。首先,由于余数小于进制基数,因此可以通过查表直接将其转换成字符串。其次,得到的商小于原整数,这使得我们离基本情况更近了一步。下一步是将 76 转换成对应的字符串。再一次运用除法,得到商 7 和余数 6。问题终于被简化到将 7 转换成对应的字符串,由于它满足基本情况 n <base(其中 base 为 10),因此转换过程十分简单。图4-3 展示了这一系列的操作。注意,我们需要记录的数字是右侧方框内的余数。
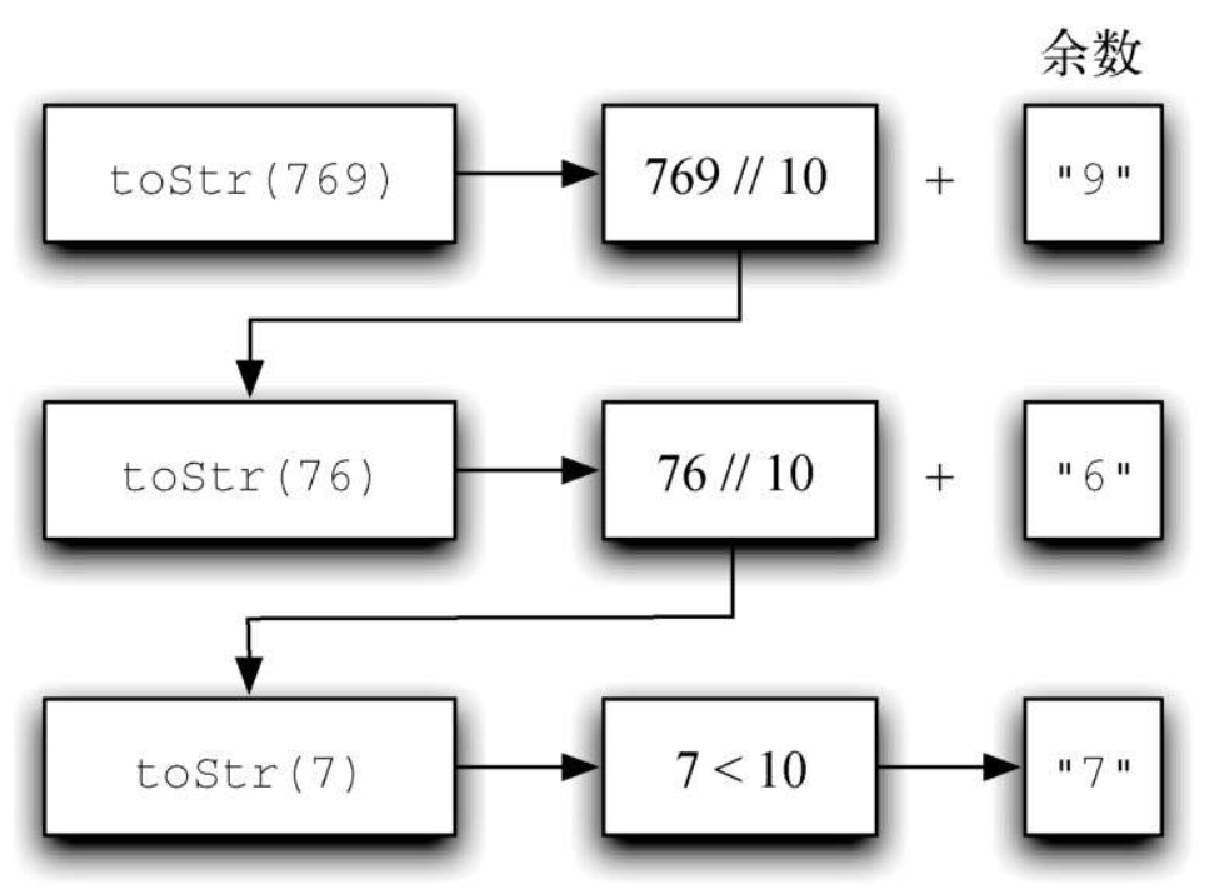
代码清单4-3 展示的 Python 代码实现了将整数转换成以 2~16 为进制基数的字符串。
代码清单4-3 将整数转换成以 2~16 为进制基数的字符串
def toStr(n,base):
convertString = "0123456789ABCDEF"
if n < base:
return convertString[n]
else:
return toStr(n//base,base) + convertString[n%base]
print(toStr(1453,16))第 4 行检查是否为基本情况,即 n 小于进制基数。如果是,则停止递归并且从 convertString 中返回字符串。第 7 行通过递归调用以及除法来分解问题,以同时满足第二条和第三条原则。
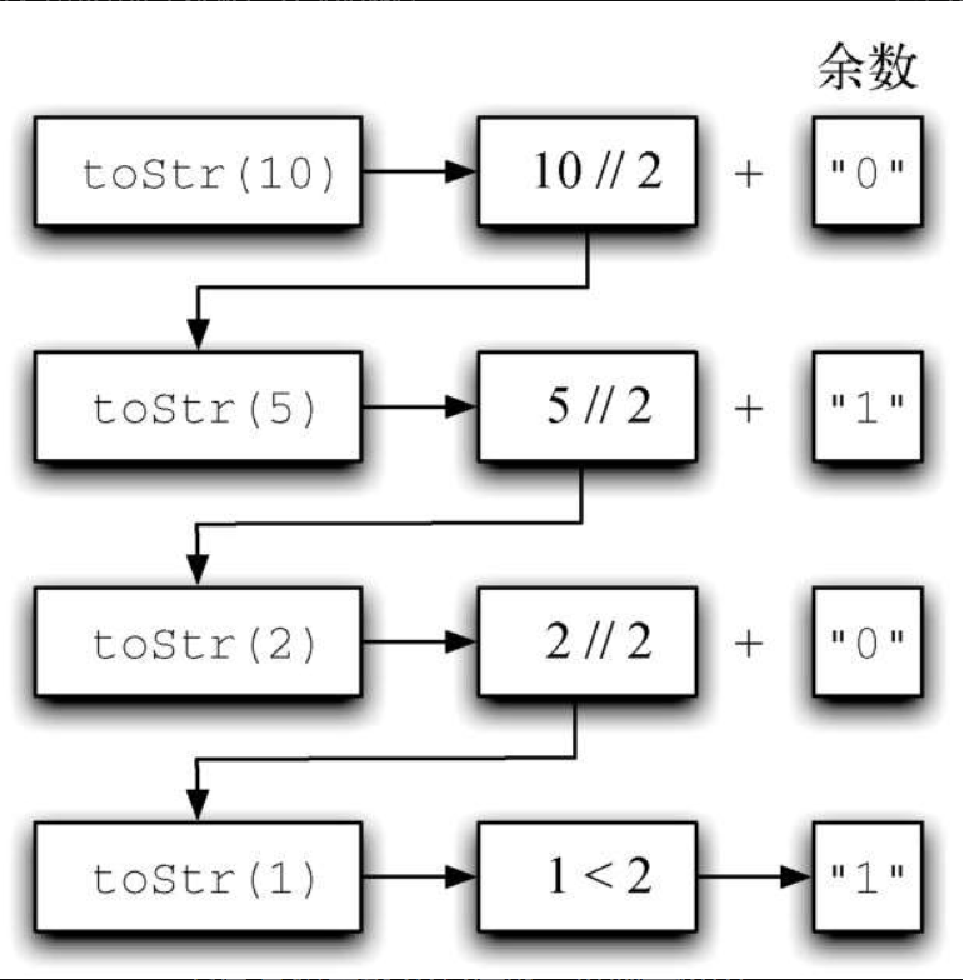
来看看该算法如何将整数 10 转换成其对应的二进制字符串 "1010"。
图4-4 展示了结果,但是看上去数位的顺序反了。由于第 7 行首先进行递归调用,然后才拼接余数对应的字符串,因此程序能够正确工作。如果将 convertString 查找和返回 toStr 调用反转,结果字符串就是反转的。但是将拼接操作推迟到递归调用返回之后,就能得到正确的结果。说到这里,你应该能想起第 3 章讨论的栈。