复习字典:跳表

字典是 Python 中用途最广的集合之一。字典也常被称作映射，它存储的是键-值对。键与某个特定的值关联，且必须是不重复的。给定一个键，映射可以返回对应的值。往映射中加入键-值对，以及根据键查询值，这些是映射的基本操作。

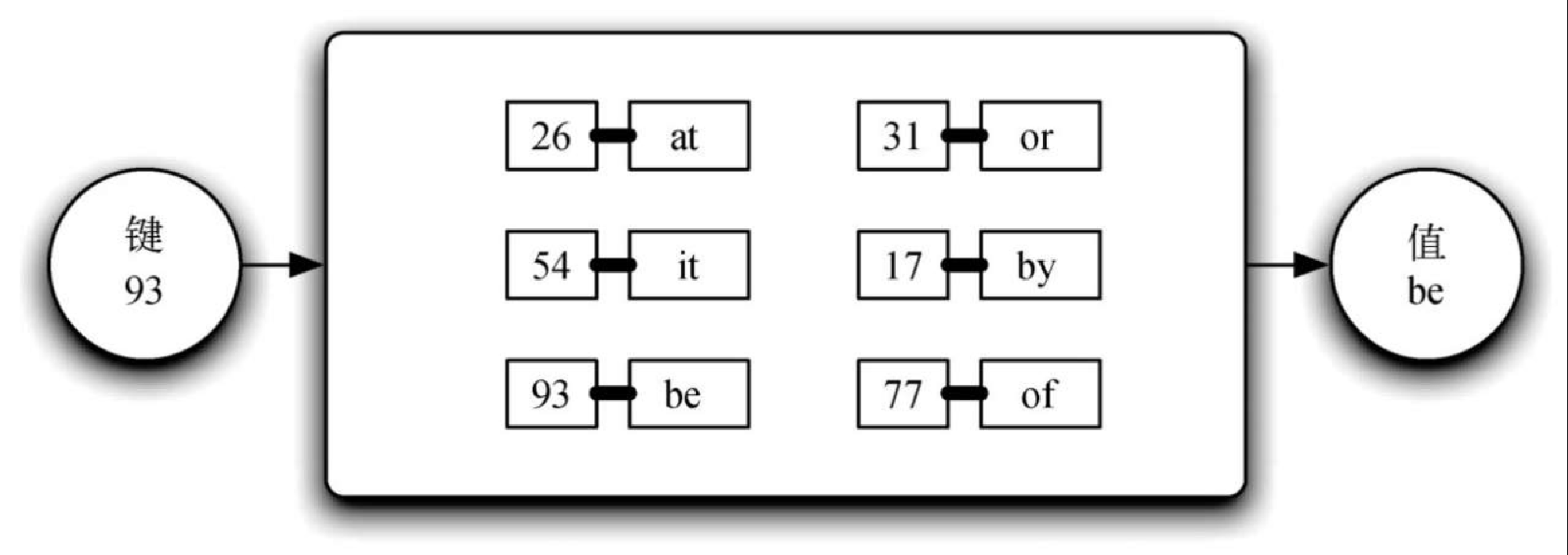
举个例子，图8-4 展示了一个包含键-值对的映射。其中，键是整数，值是由两个字母组成的单词。从逻辑角度看，对与对之间不存在顺序。不过，如果给定一个键（如93），就可以得到它所关联的值（be）。

Figure 1. 图8-4 映射示例

映射抽象数据类型

映射这一抽象数据类型由下面的结构和操作定义。如前所述，映射是键-值对的集合，可以通过键访问关联的值。映射支持以下操作。

Map() 创建一个空的映射。它不需要参数，并会返回一个空的映射集合。
put(key, value) 往映射中加入一个键-值对。需要传入键及其关联的值，没有返回值。这里假设要添加的键不在映射中。
get(key) 在映射中搜索给定的键，并返回它对应的值。

注意，映射抽象数据类型还支持其他一些操作。我们会在练习中探讨。

用Python实现字典

我们已经了解了多种实现映射的有趣方法。在第5章，我们探讨了如何用散列表实现映射。给定一组键和一个散列函数，可以将键放到集合中，并搜索和取出关联的值。我们分析过，这种搜索操作的时间复杂度是 \$O(1)\$。不过，性能会因为表的大小、冲突、冲突解决策略等因素而降低。

第 6 章探讨了用二叉搜索树实现映射。当把键存储在树中时，搜索操作的时间复杂度是 \$O(logn)\$。不过，这只有在树平衡时才成立，即树的左右子树要差不多大。不幸的是，根据插入顺序，键可能左倾或右倾，搜索性能随之下降。

本节要解决的问题就是给出一种实现方法，既能高效搜索，又能避免上述缺点。一种解决方案是使用跳表。图8-5 给出了上例的键-值对集合可能对应的一个跳表（后面会说明为什么说 “可能”）。如你所见，跳表其实就是二维链表，链接的方向向前（也就是向右）或向下。表头在图中的左上角，它是跳表结构唯一的入口。

Figure 2. 图8-5 跳表示例

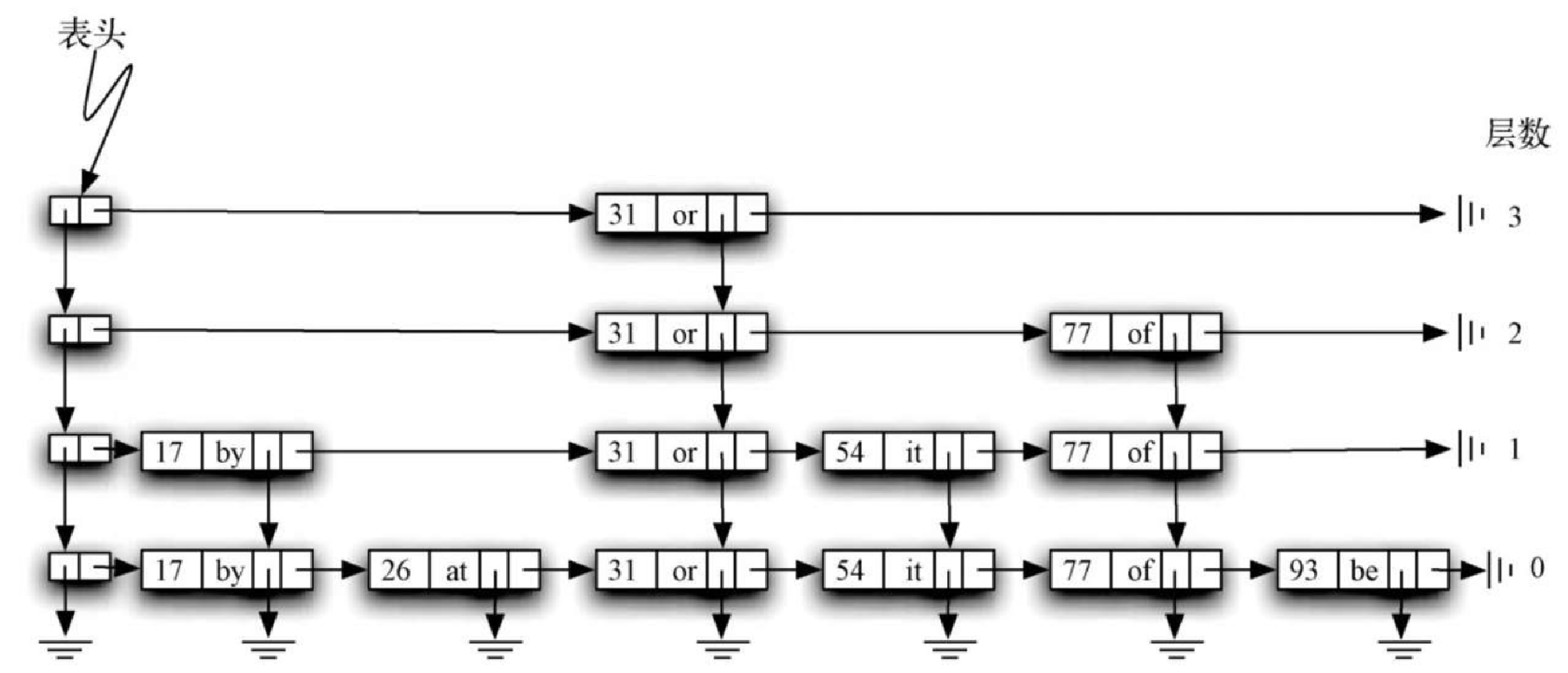
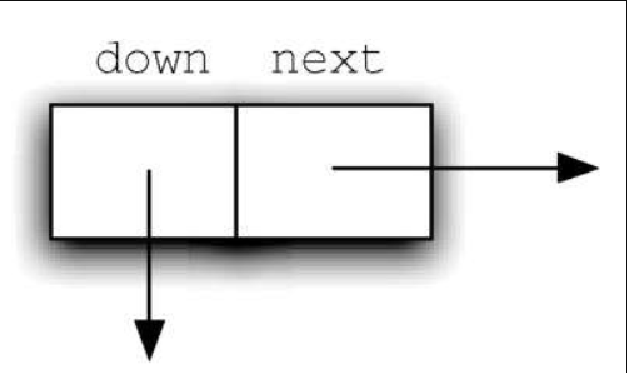
深入学习跳表之前，有必要理解一些术语的含义。图8-6 展示了跳表的主要结构，跳表由一些数据节点构成，每个节点存有一个键及其关联的值。此外，每个节点还有两个向外的引用。图8-7 展示了单个数据节点的详情。

Figure 3. 图8-6 跳表的主体由数据节点构成

Figure 4. 图8-7 单个数据节点

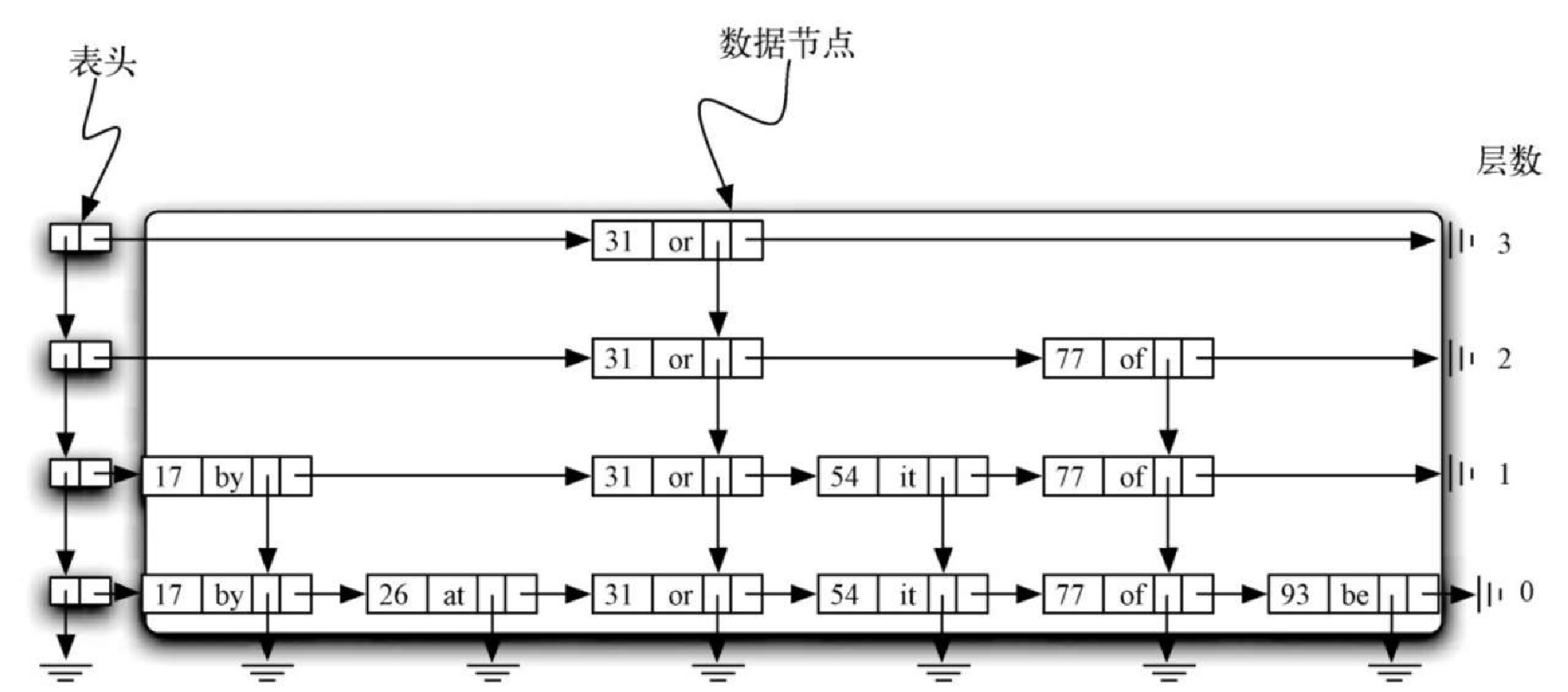
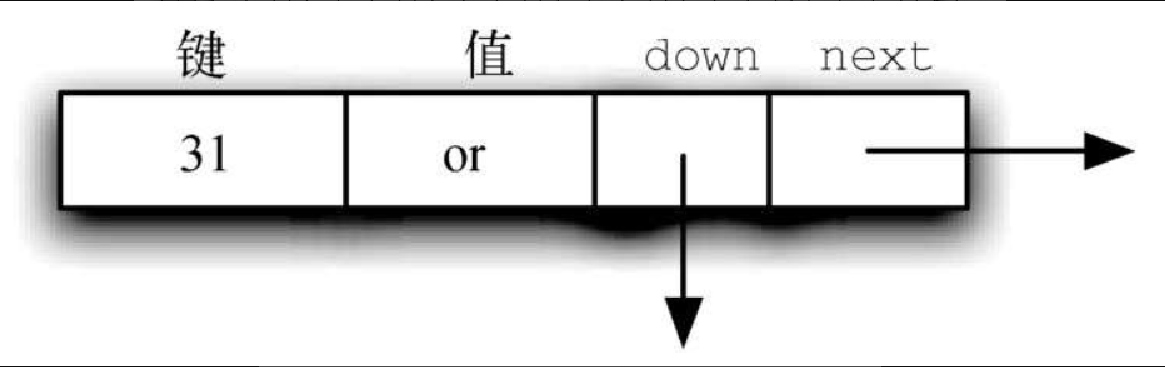
图8-8 展示了两种不同的纵列。最左边的一列由头节点的链表组成。每个头节点都有两个引用，分别是 down 和 next。down 引用指向下一层的头节点，next 引用指向数据节点的链表。图8-9 展示了头节点的详情。

Figure 5. 图8-8 头节点和塔

Figure 6. 图8-9 每个头节点都有两个引用

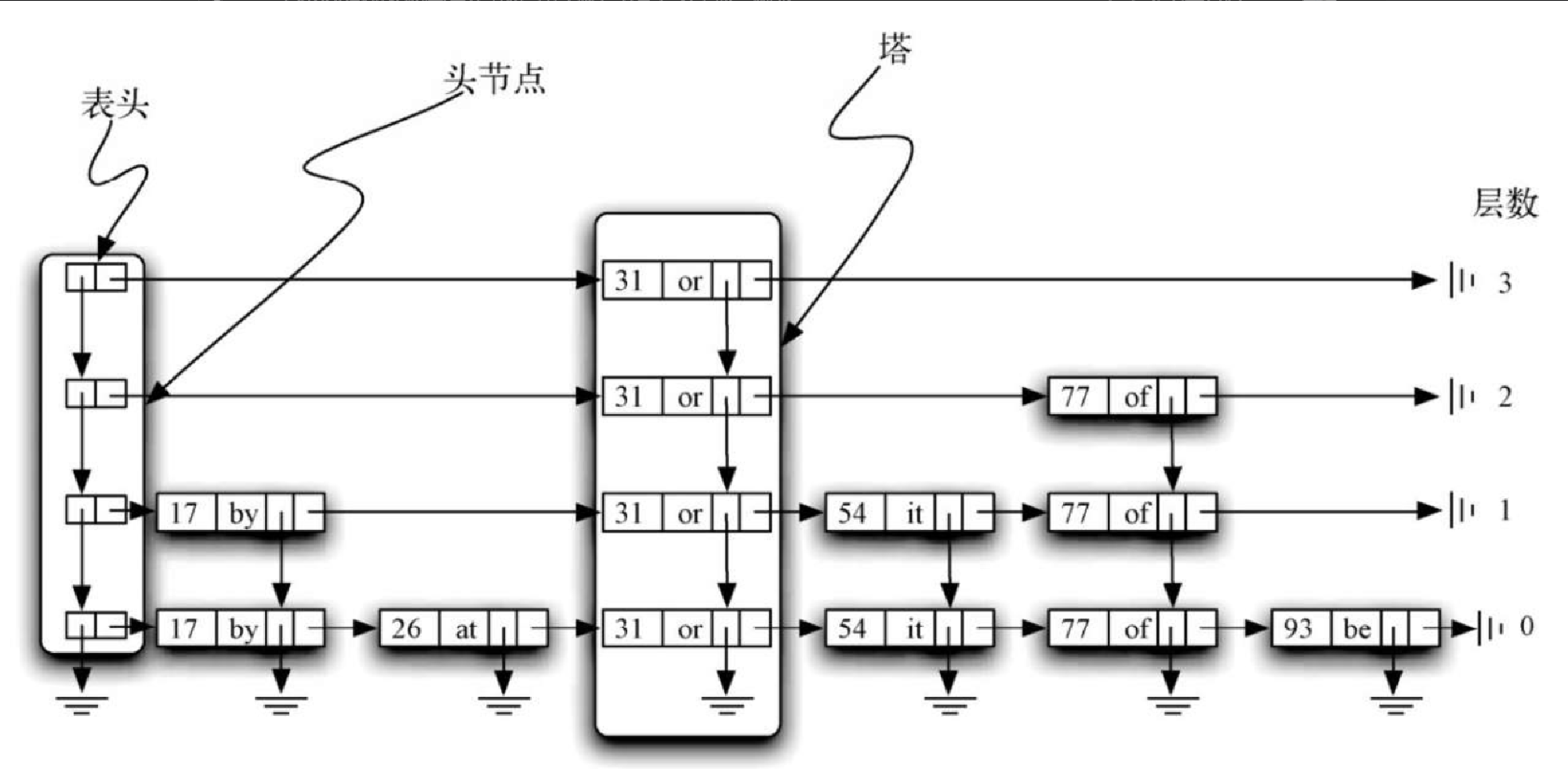
由数据节点构成的纵列称作塔。塔是由数据节点中的 down 引用连起来的。可以看出，每一座塔都对应一个键-值对，并且塔的高度不一。后文在探讨如何往跳表中添加数据时，会解释如何确定塔的高度。

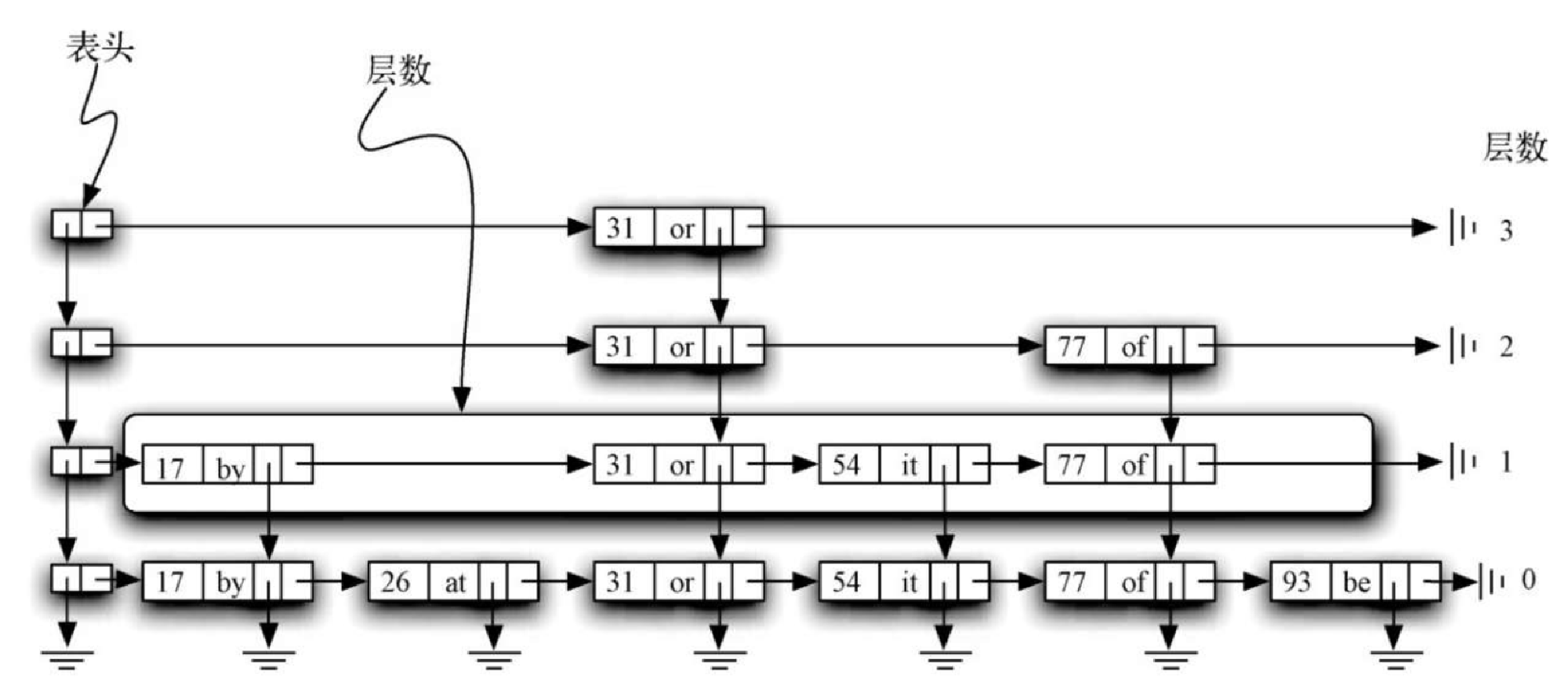
图8-10 突出展示了水平方向上的节点集合。仔细观察后会发现，每一层实际上都是由数据节点组成的有序链表，其顺序由键决定。每个链表都有自己的名字，通常用其层数指代。层数从 0 开始，底层就是第 0 层，包括整个节点集合。每个键-值对都必须出现在第 0 层的链表中。不过，层数越高，节点数就越少。跳表的这个重要特征有助于提高搜索效率。可以看到，每一层的节点数和塔的高度息息相关。

Figure 7. 图8-10 水平方向上的每一组数据节点构成一层

上述两种节点的构建方式与构建简单的链表类似。头节点（详见代码清单8-12）由 next 和 down 两个引用构成，构造方法将它们都初始化为 None。数据节点（详见代码清单8-13 ）有 4 个字段——键、值以及 next 和 down 两个引用。同样，将引用初始化为 None，并提供 get 方法和 set 方法操作节点。

代码清单8-12 HeaderNode类

class HeaderNode:
    def __init__(self):
        self.next = None
        self.down = None

    def getNext(self):
        return self.next

    def getDown(self):
        return self.down

    def setNext(self, newnext):
        self.next = newnext

    def setDown(self, newdown):
        self.down = newdown

代码清单8-13 DataNode类

class DataNode:
    def __init__(self, key, value):
        self.key = key
        self.data = value
        self.next = None
        self.down = None

    def getKey(self):
        return self.key

    def getData(self):
        return self.data

    def getNext(self):
        return self.next

    def getDown(self):
        return self.down

    def setData(self, newdata):
        self.data = newdata

    def setNext(self, newnext):
        self.next = newnext

    def setDown(self, newdown):
        self.down = newdown

代码清单8-14 给出了跳表的构造方法。刚创建时，跳表没有数据，所以没有头节点，表头被设为 None。随着键-值对的加入，表头指向第一个头节点。通过这个头节点，既可以访问数据节点链表，也可以访问更低的层。

代码清单8-14 SkipList类的构造方法

class SkipList:
    def __init__(self):
        self.head = None

搜索跳表
跳表的搜索操作需要一个键。它会找到包含这个键的数据节点，并返回对应的值。图8-11 展示了搜索键 77 的过程，星星表示搜索过程要查找的节点。

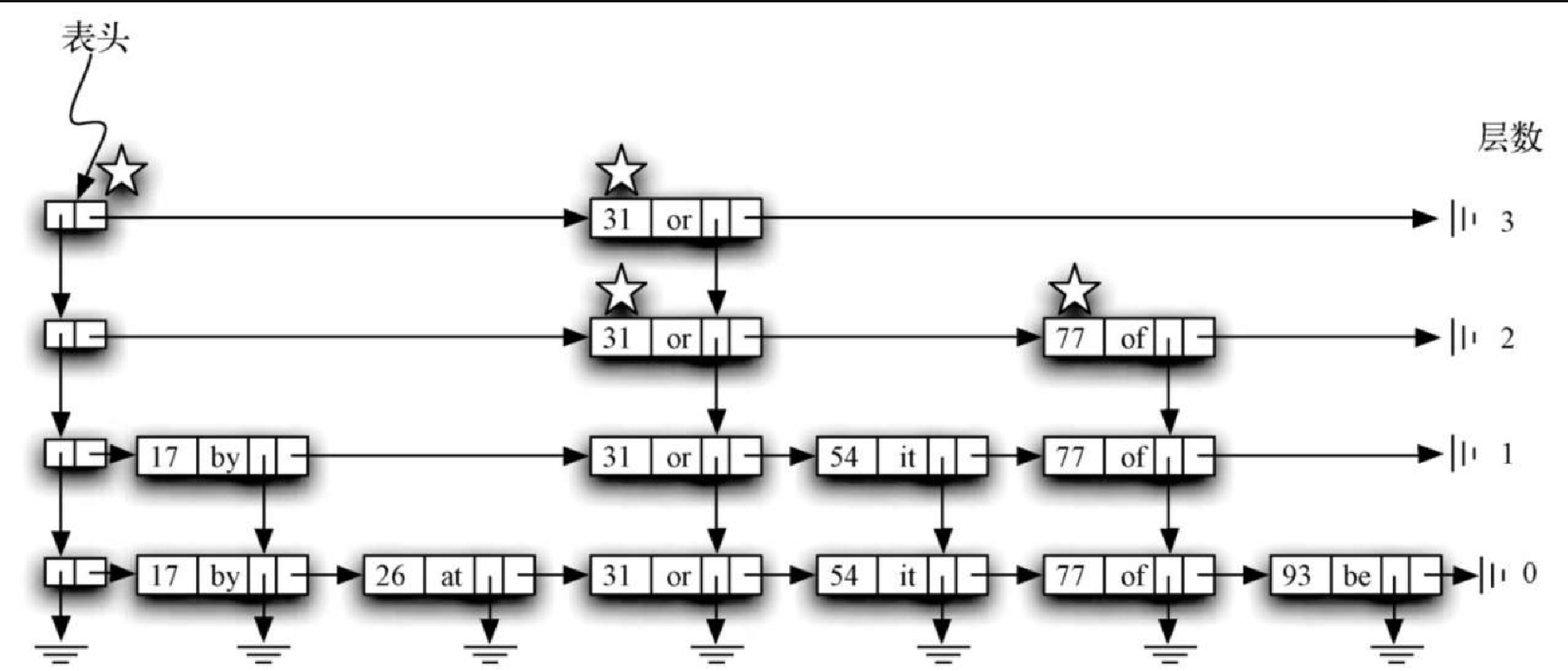Figure 8. 图8-11 搜索键77

我们从表头开始搜索 77。第一个头节点指向存储31的数据节点。因为 31 小于 77，所以向前移动。含 31 的数据节点位于第 3 层，它没有下一个节点，所以必须下降到第 2 层。在这一层，我们发现了键为 77 的数据节点。搜索成功，返回单词 of。注意，搜索过程 “跳过” 了 17 和 26。同理，可以忽略 54，从 31 直接跳到 77。

代码清单8-15 给出了 search 方法的 Python 实现。搜索从表头开始，直到找到键，或者检查完所有的数据节点。第 3 行和第 4 行的变量 found 和 stop 用于控制条件。搜索的基本思路是从顶层的头节点开始往右查找。如果没有数据节点，就下降一层（第 9 行和第 10 行）；如果有数据节点，就比较键的大小。如果匹配，就说明搜索成功，可以将 found 置为 True（第 12 行和第 13 行）。
代码清单8-15 search方法
def search(self, key): current = self.head found = False stop = False while not found and not stop: if current == None: stop = True else: if current.getNext() == None: current = current.getDown() else: if current.getNext().getKey() == key: found = True else: if key < current.getNext().getKey(): current = current.getDown() else: current = current.getNext() if found: return current.getNext().getData() else: return None
因为每一层是一个有序链表，所以不匹配的键提供了很有用的信息。如果要找的键小于数据节点中的键（第 15 行），就说明这一层不会有包含目标键的数据节点，因为往右的所有节点只会更大。这时，就需要下降一层（第 16 行）。如果已经降至底层（None），说明跳表中没有要找的键，于是将变量 stop 置为 True。另一方面，只要当前层的节点有比目标键更小的键，就往下一个节点移动（第 18 行）。

进入下一层后，重复上述过程，检查是否有下一个节点。每降一层，跳表就可以提供更多的数据节点。如果目标键在跳表中，不会到了第 0 层还不出现，因为第 0 层是完整的有序链表。我们希望通过跳表尽早地找到目标键。
往跳表中加入键-值对
在已有跳表的情况下，search 方法实现起来相对简单。本节的任务是理解如何构建跳表，以及为何以相同的顺序插入同一组键会得到不同的跳表。

要往跳表中新添键-值对，本质上需要两步。第一步，搜索跳表，寻找插入位置。记住，我们假设跳表中还没有待插入的键。图8-12 展示了试图加入键 65 的过程（值是 hi）。我们再次使用星星展示搜索过程。

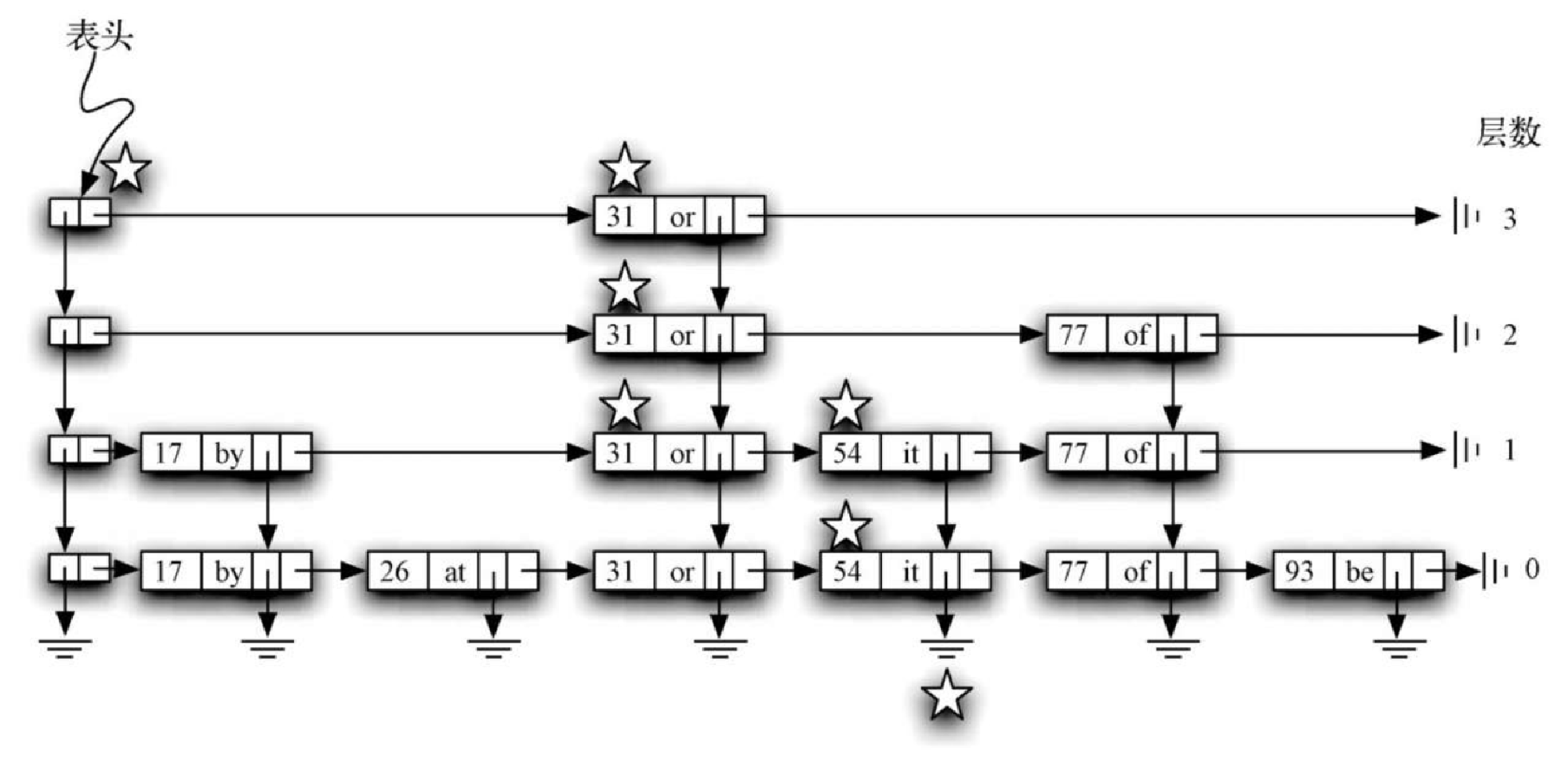Figure 9. 图8-12 搜索键65

使用和前一节一样的搜索策略，我们发现 65 比 31 大。第 3 层没有更多的节点，因此降至第 2 层。在这一层，我们发现 77 比 65 大。继续降至第 1 层，下一个节点是 54，它小于 65。继续向右，遇到 77，再往下转，遇到 None。

第二步是新建一个数据节点，并将它加到第 0 层的链表中，如图8-13 所示。然而，如果止步于此，最多只能得到一个键-值对链表。我们还需要为新的数据节点构建塔，这就是跳表的有趣之处。塔应该多高？新数据节点的塔高并不是确定的，而是完全随机的。本质上，通过 “抛硬币” 来决定是否要往塔中加一层。如果得到正面，就往当前的塔中加一层。

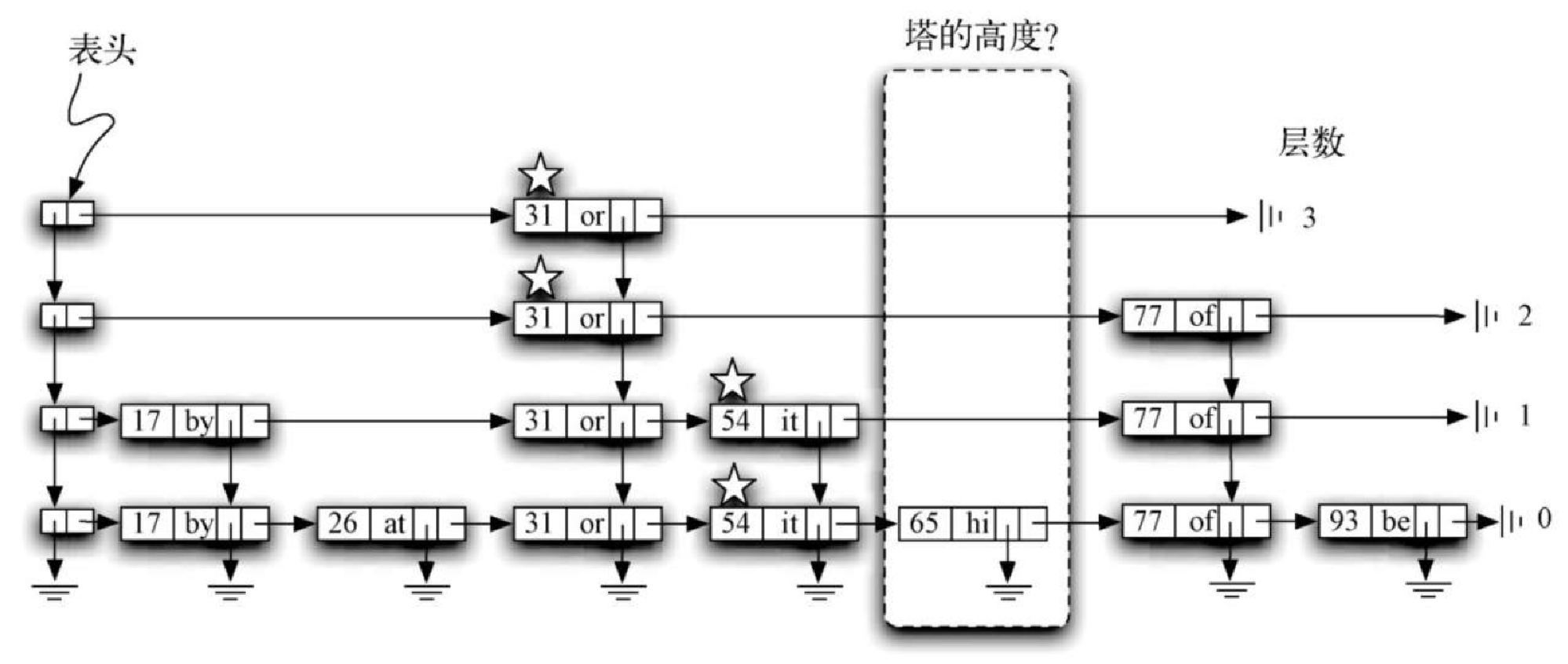Figure 10. 图8-13 为65构建数据节点和塔

利用随机数生成器可以方便地模拟抛硬币。代码清单8-16 使用 random 模块中的 randrange 函数，返回 0 或 1。如果 flip 返回 1，我们就认为得到硬币的正面。
代码清单8-16 模拟抛硬币
from random import randrange def flip(): return randrange(2)
代码清单8-17 是 insert 方法的第一部分。显然，第 2 行是在检查是否要为跳表添加第一个数据节点。在构建简单的链表时，也考虑过这个问题。如果要在表头添加节点，必须新建头节点和数据节点。第 7～14 行重复循环，直到 flip 方法返回 1（得到硬币的正面）。每新加一层，都创建一个数据节点和一个头节点。
代码清单8-17 insert方法的第一部分
def insert(self, key, data): if self.head == None: self.head = HeaderNode() temp = DataNode(key, data) self.head.setNext(temp) top = temp while flip() == 1: newhead = HeaderNode() temp = DataNode(key, data) temp.setDown(top) newhead.setNext(temp) newhead.setDown(self.head) self.head = newhead top = temp else:
如前所述，对于非空跳表（代码清单8-18），需要搜索插入位置。由于没法知道塔中会有多少个数据节点，因此需要为每一层都保存插入点。因为这些插入点会按逆序处理，所以栈可以很好地帮助我们按照与插入节点相反的顺序遍历链表。图8-13 中的星星标出了栈中的插入点，它们只表示在搜索过程中降至下一层的地方。
代码清单8-18 insert方法的第二部分
towerStack = Stack() current = self.head stop = False while not stop: if current == None: stop = True else: if current.getNext() == None: towerStack.push(current) current = current.getDown() else: if current.getNext().getKey() > key: towerStack.push(current) current = current.getDown() else: current = current.getNext() lowestLevel = towerStack.pop() temp = DataNode(key, data) temp.setNext(lowestLevel.getNext()) lowestLevel.setNext(temp) top = temp
在代码清单8-19 中，我们通过抛硬币决定塔的层数。从插入栈弹出下一个插入点。只有当栈为空之后，才需要返回并新建头节点。这些细节留给你自行研究。
代码清单8-19 insert方法的第三部分
while flip() == 1: if towerStack.isEmpty(): newhead = HeaderNode() temp = DataNode(key, data) temp.setDown(top) newhead.setNext(temp) newhead.setDown(self.head) self.head = newhead top = temp else: nextLevel = towerStack.pop() temp = DataNode(key, data) temp.setDown(top) temp.setNext(nextLevel.getNext()) nextLevel.setNext(temp) top = temp
关于跳表的结构，还有一点需要注意。之前提过，即使以相同的顺序插入同一组键，也可能得到不同的跳表。你现在应该已经知道原因了。根据抛硬币的随机本质，任意键的塔高在每次构建跳表时都会改变。
构建映射
至此，我们实现了向跳表中添加数据的操作，并且能够搜索数据。现在，终于可以实现映射抽象数据类型了。如前所述，映射支持两个操作——put 和 get。代码清单8-20 表明，可以轻松实现这两个操作，做法是构建一个内部跳表（第 3 行），并利用已经实现的 insert 方法和 search 方法。
代码清单8-20 用跳表实现Map类
class Map: def __init__(self): self.collection = SkipList() def put(self, key, value): self.collection.insert(key, value) def get(self, key): return self.collection.search(key)
分析跳表

如果简单地用一个有序链表存储键-值对，那么搜索方法的时间复杂度将是 \$O(n)\$。跳表是否会有更好的性能呢？你应该记得，跳表是基于概率的数据结构，这意味着其性能基于某些事件的概率——本例中的事件就是抛硬币。虽然详细的分析超出了本书范围，但我们可以给出一个不太正式的有力论证。

假设要为 n 个键构建跳表。我们知道，每座塔的高度从 1 开始。在添加数据节点时，假设抛出 “正面” 的概率是[插图]，我们可以说有[插图]个键的高度是 2。再抛一次硬币，有[插图]个键的高度是 3，对应连续抛出两次正面的概率。同理，有[插图]个键的高度是 4，依此类推。这意味着塔的最大高度是 \$log_2n+1\$。使用大 O 记法，可以说跳表的高度是 \$O(logn)\$。

给定一个键，在查找时要扫描两个方向。第一个方向是向下。前面的结果表明，在最坏情况下，找到目标键要查找 \$O(logn)\$ 层。第二个方向是沿着每一层向前扫描。每当遇到以下两种情况之一时，就下降一层：要么数据节点的键比目标键大，要么抵达这一层的终点。对于下一个节点，发生上述两种情况之一的概率是[插图]。这意味着查看 2 个链接后，就会下降一层（抛两次硬币后得到正面）。无论哪种情况，在任一层需要查看的节点数都是常数。因此，搜索操作的时间复杂度是 \$O(logn)\$。因为插入操作的大部分时间花在查找插入位置上，所以插入操作的时间复杂度也是 \$O(logn)\$。