复习递归

数值计算最常见的一个应用领域是密码学。每次查看银行账户，或者登录在线购物网站或计算机时，你都在应用密码学。一般来说，密码学研究的是如何加密和解密信息。本节将介绍在密码学编程中常用的一些函数。其中每一个都能用递归实现，不过在实践中可能存在更快的实现方法。

本节会用到 Python 的取余运算符（%）。你也许记得，a % b 是 a 除以 b 后剩余的部分，比如 10 % 7 = 3。任何对 10 取余的数学表达式，其结果都只能在 0～9 中。

最早的一种加密方法使用了简单的取余运算。以字符串 uryybjbeyq 为例，你能猜出原文是什么吗？代码清单8-4 给出了生成密文的代码。试试能否根据代码推导出原文。

代码清单8-4 简单的取余加密函数
def encrypt(m):
    s = 'abcdefghijklmnopqrstuvwxyz'
    n = ''
    for i in m:
        j = (s.find(i) + 13) % 26
        n = n + s[j]
    return n

encrypt 函数展示了一种被称为 “凯撒密码” 的加密形式。它还有一个描述性更强的名字，叫 rot13。encrypt 对原文中的每个字母在字母表中移动 13 个位置，如果超出字母表，就回到开头。这个函数可以轻松地由取余运算符实现。另外，字母表有 26 个字母，所以这个函数是对称的。对称性是指可以用同一个函数进行加密和解密。如果向 encrypt 函数传入字符串 uryybjbeyq，得到的就是 helloworld。

除了 13 以外，其他数字也可以，但加密和解密就不对称了。如果不对称，就需要编写解密函数 decrypt。可以让 encrypt 函数和 decrypt 函数都将轮换数作为参数。在密码学术语中，轮换参数称为 “密钥”，即移动多少位。给定消息和密钥，加密算法和解密算法就能工作了。代码清单8-5 给出了以轮换数作为参数的解密函数。作为练习，你可以尝试修改代码清单8-4 中的加密函数，使它将密钥作为参数。

代码清单8-5 使用密钥解密
def decrypt(m, k):
    s = 'abcdefghijklmnopqrstuvwxyz'
    n = ''
    for i in m:
        j = (s.find(i) + 26 - k) % 26
        n = n + s[j]
    return n

即使你只将密钥告诉接收方，这么简单的加密算法也无法长久地保护信息。接下来，我们将构建一个安全得多的加密方法——RSA 公钥加密算法。

同余定理

如果两个数 a 和 b 除以 n 所得的余数相等，我们就说 a 和 b “对模 n 同余”，记为 a≡b(mod n )。本节中的算法将利用 3 条重要的同余定理。

  • 如果 a≡b(mod n )，那么 ∀c, a+c≡b+c(mod n)。

  • 如果 a≡b(mod n)，那么 ∀c, ac≡bc(mod n)。

  • 如果 a≡b(mod n)，那么 ∀p, p>0, ap≡bp(mod n)。

幂剩余

假设我们想知道 31254906 的最后一位数。问题在于，不仅计算量大，而且使用 Python 的 “无限精度” 整数，这个数字有 598743 位！但是，我们只想知道最后一位数。这其实是两个问题：一、如何高效地计算xn？二、如何能在不必算出所有 598743 位数的前提下，计算xn(mod p)？

运用上述第 3 条同余定理，不难解决第 2 个问题。

  1. 将 result 初始化为 1。

  2. 重复 n 次：

    • 用 result 乘以 x；

    • 对 result 进行取余运算。

这样就简化了计算，因为我们一直让 result 保持为一个较小的值，而不是精确地算出最终结果。但是，利用递归还能做得更好。

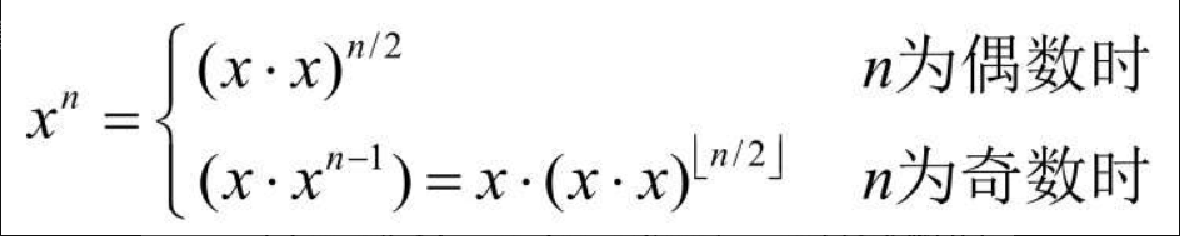
image 2023 12 14 11 13 32 828

对于浮点数 n，向下取整[插图]得到的是小于 n 的最大整数。Python 的整数除法就是对除法结果向下取整，所以不必额外编写代码。以上等式为计算 xn 给出了很好的递归定义。现在只缺基本情况。你应该记得，对于任意数 x，有 x0=1。由于每次递归调用都会减小指数，因此 n=0 就是很好的基本情况。

在以上等式中，奇数和偶数的情况都有因子[插图]，所以对它的计算不做条件判断，并将它存到变量 tmp 中。还要注意一点，每一步都进行取余运算。在代码清单8-6 的实现中，结果始终较小，乘法运算的次数也比纯循环方案要少得多。

代码清单8-6 xn(mod p )的递归定义
def modexp(x, n, p):
    if n == 0:
        return 1
    t = (x * x) % p
    tmp = modexp(t, n // 2, p)
    if n % 2 != 0:
        tmp = (tmp * x) % p
    return tmp

最大公因数与逆元

正整数 x 关于模 m 的逆元 a 满足 ax≡1(mod m)。比如 x=3, m=7, a=5, 3×5=15, 15%7=1，所以 5 是 3 关于模 7 的逆元。乍一看，逆元 这个概念令人困惑。这个例子中的 5 是怎么选出来的呢？5 是 3 关于模 7 的唯一逆元吗？给定任意数 m，所有的数都有逆元吗？

我们来看个例子，可能会对解答第一个问题有所启发。请看下面这个 Python 会话：

>>> for i in range(1, 40):
...      if (3 * i) % 7 == 1:
...           print i
...
5
12
19
26
33

这个小实验告诉我们，当 x=3、m=7 时，存在多个逆元：5, 12, 19, 26, 33, …。对这个数列，你发现什么有趣之处了么？其中每个数都是模 7 的某个倍数减 2。

对于任意的 x 和 m，都存在逆元吗？来看另一个例子。假设 x=4,m=8。如果将 4 和 8 插入前一个例子的循环中，什么也得不到。如果去掉条件判断语句，打印 (4 * i) %8 的结果，就得到数列 0, 4, 0, 4, 0, 4, …。0 和 4 交替出现，但显然永远不会出现 1。如何预知这一点呢？

答案是，当且仅当 m 和 x 互素时，x 关于模 m 才有逆元。互素是指 gcd(m, x)=1。你应该记得，两个数的最大公因数（greatest common divisor, GCD）是能整除它们的最大整数。那么，如何计算两个数的最大公因数呢？

给定两个数 a 和 b，要找到它们的最大公因数，可以反复计算 a-b，直到 a<b。当 a<b 时，交换 a 和 b。当 a-b=0 时，再次交换。此时，gcd(a,0)=a。这就是欧几里得算法，它已经有2000多年的历史了。

在用于设计递归时，欧几里得算法非常简单。基本情况就是 b=0。有两种递归调用：若 a<b，交换 a 和 b，发起递归调用；否则，在递归调用时用 a-b 替换 a。代码清单8-7 给出了欧几里得算法的实现。

代码清单8-7 利用欧几里得算法求最大公因数
def gcd(a, b):
    if b == 0:
        return a
    elif a < b:
        return gcd(b, a)
    else:
        return gcd(a-b, b)

尽管欧几里得算法易于理解和编程，但还不够高效，在 a>b"> 时尤其如此。不过，模运算又一次派上用场。当 a-b<b 时，减法结果等于 a 除以 b 的余数。明白了这一点，就可以去掉减法，而仅用一个递归调用交换 a 和 b。代码清单8-8 给出了改良后的算法。

代码清单8-8 改良后的欧几里得算法
def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)

现在我们有了判断是否有逆元的方法，下一个任务就是实现能高效地计算出逆元的算法。假设对于任意数 x 与 y，我们都可以计算出 gcd(x, y) 以及一对整数 a 和 b，满足 d=gcd(x, y)=ax+by。比如，1=gcd(3,7)=-2×3+1×7，所以 -2 和 1 就可以分别作为 a 和 b 的解。使用前一个例子中的 m 和 x 来替换 x 和 y，得到 1=gcd(m,x)=am+bx。由本节开头的讨论可知，bx≡1(mod m)，所以 b 是 x 关于模 m 的一个逆元。

我们已经将计算逆元的问题简化为寻找满足等式 d=gcd(x, y)=ax+by 的整数 a 和 b。既然一开始通过 gcd 函数解决这个问题，那么就让我们通过扩展它来收尾吧。取两个数 x>=y，返回元组 (d, a, b)，满足 d=gcd(x, y) 且 d=ax+by。对 gcd 函数的扩展如代码清单8-9 所示。

代码清单8-9 扩展gcd函数
def ext_gcd(x, y):
    if y == 0:
        return x, 1, 0
    else:
        (d, a, b) = ext_gcd(y, x % y)
        return d, b, a - (x // y) * b

为了理解扩展后的 gcd 函数，来看一个例子。假设 x=25, y=9。图8-3 展示了这个递归函数的调用和返回值。

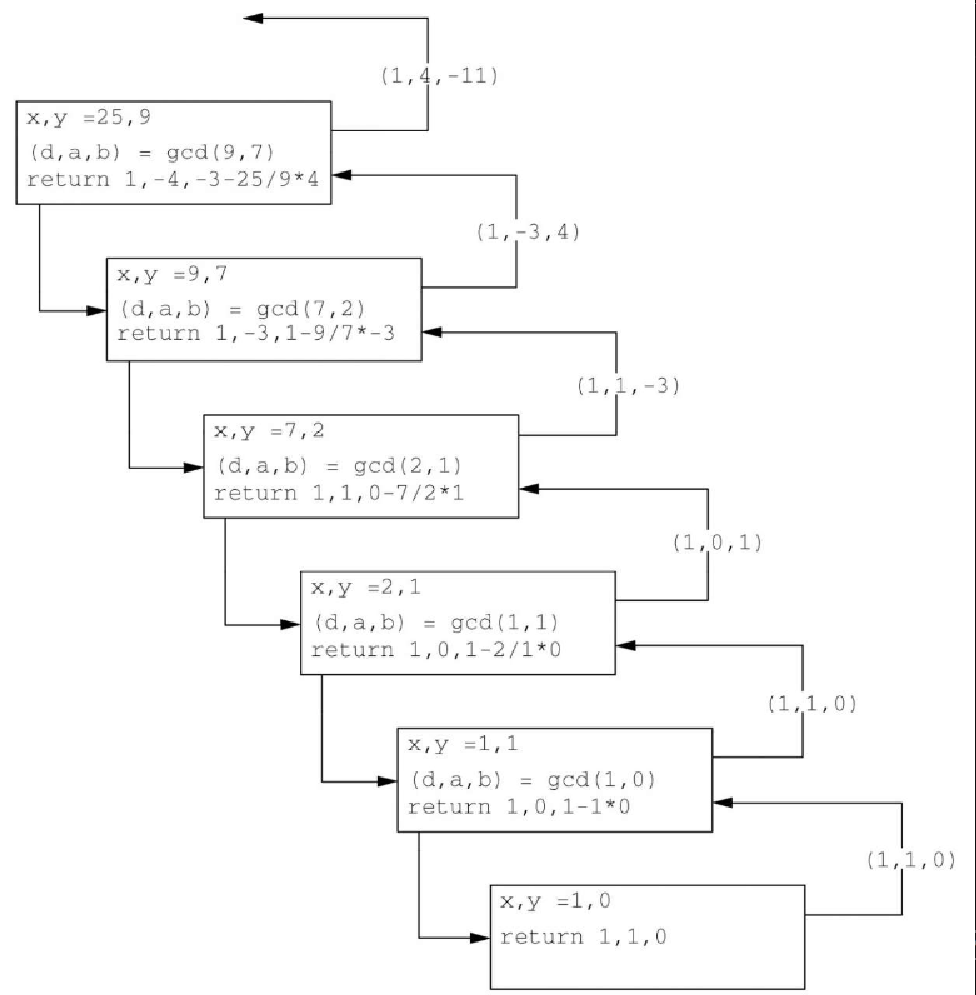
image 2023 12 14 11 28 50 852
Figure 1. 图8-3 ext_gcd函数的调用树

与原始的欧几里得算法一样，当基本情况 y=0 出现时，返回 d=x。不过，还返回了另两个值：a=1 与 b=0。这 3 个值满足 d=ax+by。如果 y>0，就递归计算 (d, a,b)，使得 d=gcd(y, x mod y) 且 d=ay+b(x mod y)。和原始算法一样，d=gcd(x,y)。但另两个值 a 和 b 呢？我们知道，a 和 b 一定是整数，因此分别记为 A 和 B，也就有 d=Ax+By。为了计算 A 和 B，重新整理等式：

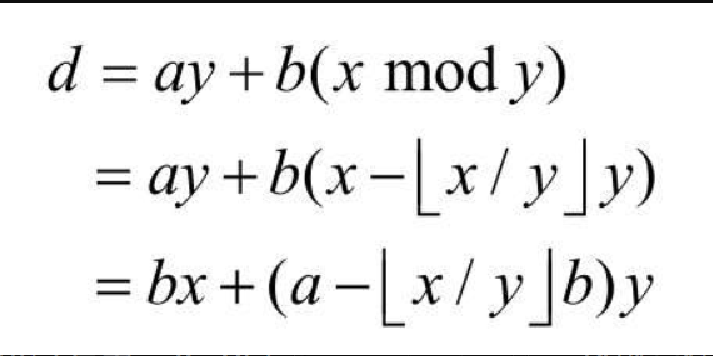
image 2023 12 14 11 30 15 899

注意，[插图]。这没问题，因为这就是计算 x/y(x mod y) 余数的方式。从最后的等式可以看出，A=b且[插图]。这就是代码清单8-9 第 6 行所做的！注意，算法中每一步返回的值都满足 d=ax+by。

RSA算法

至此，我们已经备齐了编写 RSA 算法所需的全部工具。可以说，RSA 算法是最易于理解的公钥加密算法。公钥加密的概念由 Whitfield Diffie、Martin Hellman 和 Ralph Merkle 提出，它对密码学的主要贡献在于密钥成对的思想：加密密钥用于明文到密文的转换，解密密钥用于密文到明文的转换。密钥都是单向的，所以用私钥加密的信息只能用公钥解密，反之亦然。

RSA 算法的安全性来自于大数分解的难度。公钥和私钥由一对大素数（100～200位）得到。既然 Python 中有原生的长整数，那么 RSA 算法实现起来就十分有趣且容易。要生成两个密钥，选两个大素数 p 和 q，并计算它们的乘积。

\$n= p×q\$

下一步是随机选择加密密钥 e，使得 e 与 (p-1)×(q-1) 互素。

\$gcd (e, (p-1)×(q-1))=1\$

加密密钥 d 就是 e 关于模 (p-1)×(q-1) 的逆元。在这里，可以使用欧几里得算法的扩展版本。

e 和 n 一起组成公钥，d 则是私钥。算出 e、n 和 d 之后，最初的素数 p 和 q 就没用了，但仍然不应该泄露它们。

加密时，只需使用 c=me(mod n)。解密时，则使用 m=cd(mod n)。如果记得 d 是 e(mod n) 的逆元，就很容易理解。

\$c^d=(m^e)^d(mod n)\$
\$=m^(ed)(mod n)\$
\$=m^1(mod n )\$
\$=m(mod n )\$

在将等式转化为 Python 代码之前，需要讨论一些细节。如何将 hello world 这样的文本信息转化成数字？最简单的方法就是把每个字符的 ASCII 值拼接起来。不过，由于十进制的 ASCII 值位数不固定，因此使用十六进制，因为我们确信两位的十六进制数代表一字节或一个字符。

 h   e   l   l   o      w   o   r   l   d
104 101 108 108 111 32 119 111 114 108 100
68   65  6c  6c  6f 20  77  6f  72  6c  64

拼接所有的十六进制数，再将得到的大数转换为十进制整数。

m=126207244316550804821666916

Python 可以很好地处理这个大数。但实际使用 RSA 算法加密的程序会将明文切分成小块，对每一块加密，这样做有两个原因。第一个原因是性能。即使一条较短的电子邮件消息，比如大小为 1K 的文本，生成的数也会有 2000～3000 位！如果再取 d 次方——d 有 10 位——这可是一个相当大的数！

第二个原因是限制条件 m≤n。必须确保消息的模 n 表示是唯一的。举例来说，p 和 q 分别取 5563 和 8191。n=5563×8191=45566533。为了保持分块的整数小于 m，我们将消息切分成小于表示 n 所需的字节数。在 Python 中使用整型方法 bit_length 很容易得到位数。有了表示数字所需的位数，除以 8 就是字节数。消息中的每个字符都由一字节表示，这个除法告诉我们的就是每一块的字节数。因此，可以方便地将消息分成 n 个字符的块，将每一块的十六进制表示转换成整数。本例中，可以使用 26 位表示 45566533。使用整数除法除以 8，得知应该将消息切分成 3 个字符的块。

字符 h、e 和 l 的十六进制值分别是 68、65 和 6c，拼起来就是 68656c，转成整数就是 6841708。

\$m^1=6841708\$
\$m^2 =7106336\$
\$m^3 =7827314\$
\$m^4 =27748\$

注意，切分消息可能会很复杂，当转换后得到的数字不足 7 位时尤其如此。在这种情况下，拼接时要在结果前小心地补上 0。

现在选择 e 的值。可以随机取值，并用 (p-1)×(q-1)=45552780 检验。记住，e 和 45552780 互素。对于这个例子，1471 就很合适。

d=ext_gcd(45552780,1471)
=-11705609
=45552780-11705609
=33847171

我们用这一信息来加密第一个消息块：

\$c=6841708^1471(mod 45566533)=16310024\$

解密 c，确保能得到原来的值：

\$m=16310024^33847171(mod 45566533)=6841708\$

可以用同样的过程加密剩下的块，然后一起作为密文发送。

接下来看 3 个 Python 函数，如代码清单8-10 所示。RSAgenKeys 根据 p 和 q 创建一个公钥和一个私钥。RSAencrypt 接受一段消息、公钥和 n，并返回密文。RSAdecrypt 接受密文、私钥和 n，并返回原始消息。

以下是运行结果的示例。

>>> e, d, n = RSAgenKeys(5563, 8191)
>>> c = RSAencrypt('goodbye girl', e, n)
>>> c
[17194224, 5988784, 2786637, 23090820]
>>> m = RSAdecrypt(c, d, n)
>>> m
'goodbye girl'
代码清单8-10 RSA算法的实现
 def RSAgenKeys(p, q):
     n = p * q
     pqminus = (p - 1) * (q - 1)
     e = int(random.random() * n)
     while gcd(pqminus, e) != 1:
         e = int(random.random() * n)
     d, a, b = ext_gcd(pqminus, e)
     if b < 0:
        d = pqminus + b
     else:
        d = b
     return ((e, d, n))


 def RSAencrypt(m, e, n):
     chunks = toChunks(m, n.bit_length() // 8 * 2)
     encList = []
     for messChunk in chunks:
        c = modexp(messChunk, e, n)
        encList.append(c)
     return encList


 def RSAdecrypt(chunkList, d, n):
     rList = []
     for c in chunkList:
        m = modexp(c, d, n)
        rList.append(m)
     return chunksToPlain(rList, n.bit_length() // 8 * 2)

最后看两个将字符串切分成块的辅助函数，它们利用了 Python 3.x 的一个新特性：字节数组可以将字符串存储为字节序列。这样一来，就可以方便地进行字符串与十六进制序列之间的转换。

从代码清单8-11 中可以看到将字符串转换为数字块列表的过程。有一点要注意，必须确保字符对应的十六进制数一直是两位。这意味着有时需要补零，可以用字符串格式化表达式 '%02x' % b 轻松搞定。这个表达式创建包含两个字符的字符串，并且在必要时在前面补零。根据整条消息得到一个长的十六进制字符串后，可以将长串切分成 numChunks 个十六进制数块。这就是 for 循环要做的工作。最后用 eval 函数和列表解析式将每个十六进制数转换为整数。

代码清单8-11 将字符串转换为数字块列表
def toChunks(m, chunkSize):
    byteMess = bytes(m, 'utf-8')
    hexString = ''
    for b in byteMess:
        hexString = hexString + ("%02x" % b)

    numChunks = len(hexString) // chunkSize
    chunkList = []
    for i in range(0, numChunks * chunkSize + 1, chunkSize):
        chunkList.append(hexString[i:i + chunkSize])
    chunkList = [eval('0x' + x) for x in chunkList if x]
    return chunkList


def chunksToPlain(clist, chunkSize):
    hexList = []
    for c in clist:
        hexString = hex(c)[2:]
        clen = len(hexString)
        hexList.append('0' * ((chunkSize - clen) % 2)
                       + hexString)

    hstring = "".join(hexList)
    messArray = bytearray.fromhex(hstring)
    return messArray.decode('utf-8')

将加密块转换回字符串，和创建一个长的十六进制字符串并转换为 bytearray 一样容易。bytearray 内置的 decode 函数将字节数组转换为字符串。唯一需要注意的是，块表示的数字可能明显小于原始的数字。在这种情况下，需要补零，以确保所有块在拼接时是等长的。通过 '0' *((chunkSize - clen) % 2) 把零前置，其中 chunkSize 是字符串中应有的位数，clen 则是实际的位数。