复习Python列表

第 2 章介绍了 Python 列表的一些大 O 性能限制。不过，我们还不了解 Python 是如何实现列表数据类型的。在第 3 章中，你学习了如何用 “节点与引用” 模式实现链表。但 “节点与引用” 的实现在性能上仍然不及 Python 列表。本节将探讨 Python 列表的实现原则。记住，Python 列表其实是用 C 语言实现的，本节旨在用 Python 阐释关键思路，而不是取代 C 语言的实现。

实现 Python 列表的关键在于使用数组，这种数据类型在 C、C++、Java 及其他许多编程语言中都很常见。数组很简单，它只能存储同一类型的数据。比如，可以定义一个整数数组，也可以定义一个浮点数数组，但不能合二为一。数组只支持两种操作：索引和对某个元素赋值。

理解数组的最佳方式是将它看作内存中连续的字节块。可以切分这个字节块，每一小块占 n 字节，n 由数组元素的数据类型决定。图8-1 展示了存储 6 个浮点数的数组。

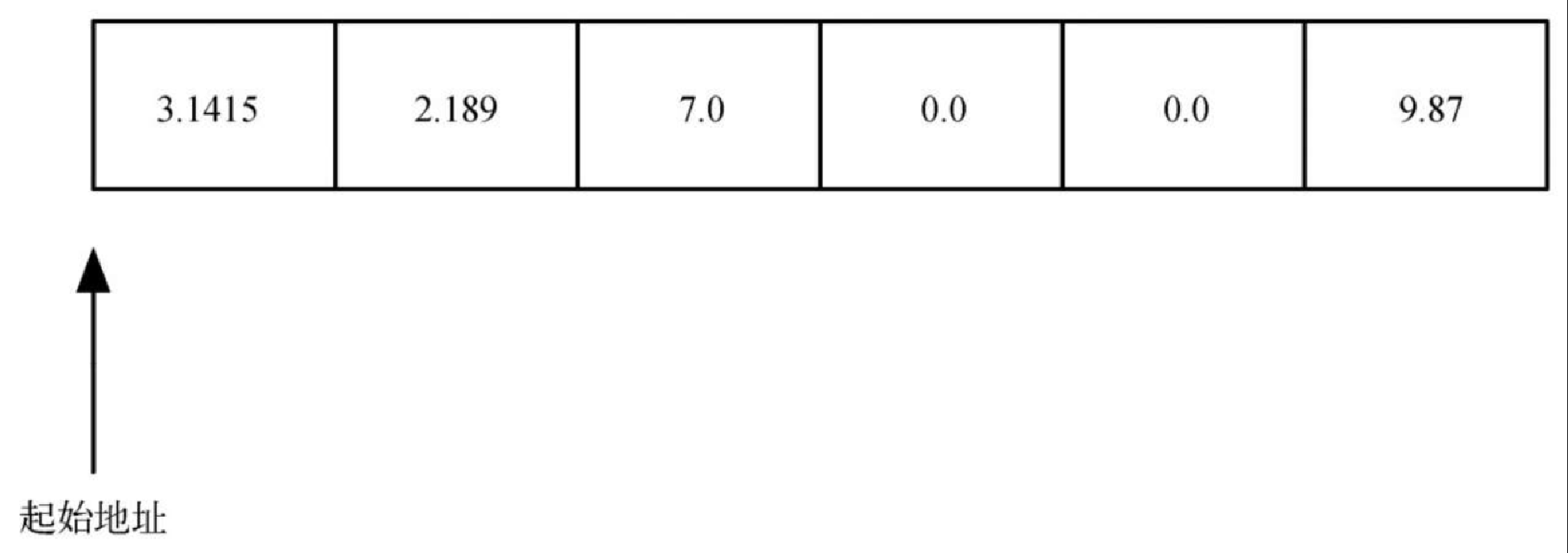
image 2023 12 14 10 07 19 344
Figure 1. 图8-1 浮点数数组

在 Python 中，每个浮点数占 16 字节。因此，图8-1 中的数组共占 96 字节。起始地址是指数组在内存中的起始地址。你一定见过 Python 对象的内存地址，比如 <__main__.Foo object at 0x5eca30> 说明对象 Foo 存储于内存地址 0x5eca30。地址很重要，因为数组的索引运算是通过以下这个非常简单的算式实现的：

元素地址 = 起始地址 + 元素下标 × 元素大小

假设浮点数数组的起始地址是 0x000040，对应的十进制数是 64。要计算数组中位置 4 的元素的地址，只需做算术题：64 + 4 × 16 = 128。显然，这种计算的时间复杂度是 \$O(1)\$，但是存在一些风险。首先，数组大小是固定的，不能在数组末尾无限制地附加元素。其次，包括 C 在内的一些语言不检查数组的边界，所以即使数组只有 6 个元素，使用下标 7 赋值也不是运行时错误。可见，这会带来难以追踪的问题。在 Linux 操作系统中，数组访问越界会得到一条信息量并不充分的报错消息：“存储器区块错误”。

Python 使用数组实现链表的策略大致如下：

  • 使用数组存储指向其他对象的引用（在 C 语言中称为指针）；

  • 采用过度分配策略，给数组分配比所需的更大的空间；

  • 数组被填满后，分配一个更大的数组，将旧数组的内容复制到新数组中。

这个策略的效率很高。在动手实现或证明之前，先看看它的时间复杂度：

  • 索引运算和赋值都是 \$O(1)\$；

  • 追加操作在普通情况下是 \$O(1)\$，在最坏情况下是 \$O(n)\$；

  • 从列表尾弹出元素是 \$O(1)\$；

  • 从列表中删除元素是 \$O(n)\$；

  • 将元素插入任意位置是 \$O(n)\$。

让我们通过一个简单的例子来理解上述策略。首先只实现构造方法、__resize 方法和 append 方法，类名为 ArrayList。构造方法要初始化两个实例变量：maxSize 记录当前数组的大小，lastIndex 记录当前列表的末尾。由于 Python 没有数组数据类型，因此我们将使用列表来模拟数组。代码清单8-1 列出了这 3 个方法。注意，构造方法先初始化上述两个实例变量，然后创建一个不包含元素的数组 myArray。此外，构造方法还会创建一个名为 sizeExponent 的实例变量。稍后将学习这个变量的用法。

代码清单8-1 使用数组实现列表的简单示例
class ArrayList:

    def __init__(self):
        self.sizeExponent = 0
        self.maxSize = 0
        self.lastIndex = 0
        self.myArray = []

    def append(self, val):
        if self.lastIndex > self.maxSize - 1:
            self.__resize()
        self.myArray[self.lastIndex] = val
        self.lastIndex += 1

    def __resize(self):
        newsize = 2 ** self.sizeExponent
        print("newsize = ", newsize)
        newarray = [0] * newsize
        for i in range(self.maxSize):
            newarray[i] = self.myArray[i]

        self.maxSize = newsize
        self.myArray = newarray
        self.sizeExponent += 1

append 方法做的第一件事（第 10 行）就是检测 lastIndex 是否超出了数组允许的下标范围。如果超过，就调用 __resize。注意，我们使用约定俗成的双下划线，以确保 resize 是私有方法。数组扩容后，新值被加到列表的 lastIndex 处，lastIndex 则加 1。

__resize 方法通过 2sizeExponent 计算出新的数组大小。扩容数组有很多种方法，有些每次将数组扩大一倍，有些乘以 1.5，有些则使用 2 的幂。Python 采用的方法是乘以 1.125 加一个常数。Python 的开发人员之所以设计这样的策略，是为了在各种 CPU 和内存的速度间取得平衡。根据这个策略，数组大小是这样的序列：0, 4, 8,16, 25, 35, 46, 58, 72, 88, … 每次扩容都会浪费一些空间，但便于分析。分配新数组后，要将旧列表中的值复制到新数组中，在第 20 行开始的循环做的正是这项工作。最后，必须更新 maxSize 和 lastIndex，增加 sizeExponent，并将 newarray 保存为 self.myArray。在 C 语言中，self.myArray 对旧内存块的引用要显式地返回给系统，以供回收利用。但是，不再被引用的 Python 对象会自动地被垃圾回收算法清理。

继续学习之前，先分析为什么 append 在普通情况下的时间复杂度是 \$O(1)\$。在大部分情况下，追加元素 ci 的时间代价是 1。只有在 lastIndex 是 2 的幂时，代价才会变得更昂贵，即 \$O(l\a\stIndex)\$。可以将插入第 i 个元素的代价总结如下：

image 2023 12 14 10 47 46 431

由于复制 lastIndex 个元素的情况相对较少，因此可以将它的代价均分——也叫作均摊——到所有追加操作上。这样一来，追加操作的平均时间复杂度就变为 \$O(1)\$。举个例子，考虑已经加了 4 个元素的情况。对于大小为 4 的数组，此前的每次追加操作都只需向数组中存储一个元素即可。在追加第 5 个元素时，Python 分配一个大小为 8 的新数组，并将原来的 4 个元素复制过来。不过，现在多出一些空间，可供进行 4 次低代价的追加操作。用数学公式表示如下：

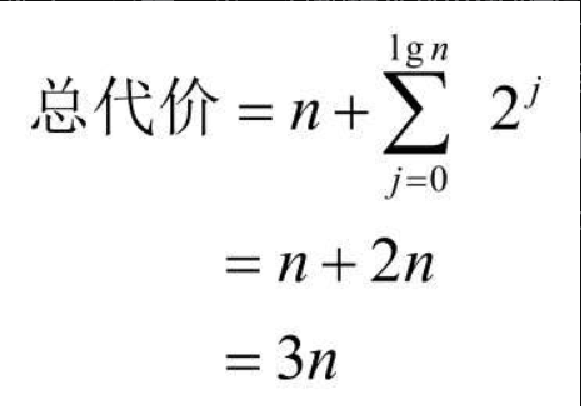
image 2023 12 14 10 49 50 398

以上等式中的累加可能不容易理解，我们来仔细研究。此处的累加是从 0 加到以 2 为底 n 的对数。上界告诉我们需要给数组扩容多少次。2j 表明数组扩容时要复制多少次。既然追加 n 个元素的总代价是 3n，那么平均到每个元素就是 3n/n=3。这是一个常数，所以我们说时间复杂度是 \$O(1)\$。这种分析被称为 均摊分析，它在分析高级算法时很有用。

下面讨论索引操作。代码清单8-2 给出了索引和赋值的 Python 实现。前面讨论过，要找到数组中第 i 个元素的内存地址，只需使用一个时间复杂度为 \$O(1)\$ 的算式。即使是 C 语言，也将这个算式隐藏在一个漂亮的数组索引运算符背后。在这一点上，C 和 Python 倒是达成了一致。实际上，Python 在这样的运算中很难获取对象实际的内存地址，所以我们使用列表内置的索引运算符。如果你对此有疑惑，可以查看 Python 源代码中的 listobj.c 文件。

代码清单8-2 索引操作
 def __getitem__(self, idx):
     if idx < self.lastIndex:
        return self.myArray[idx]
     else:
        raise LookupError('index out of bounds')


 def __setitem__(self, idx, val):
     if idx < self.lastIndex:
        self.myArray[idx] = val
     else:
        raise LookupError('index out of bounds')

最后来看看代价更昂贵的插入操作。往 ArrayList 中插入元素时，需要先将从插入点起的所有元素往前挪一位，从而为待插元素腾出空间。图8-2 展示了这个过程。

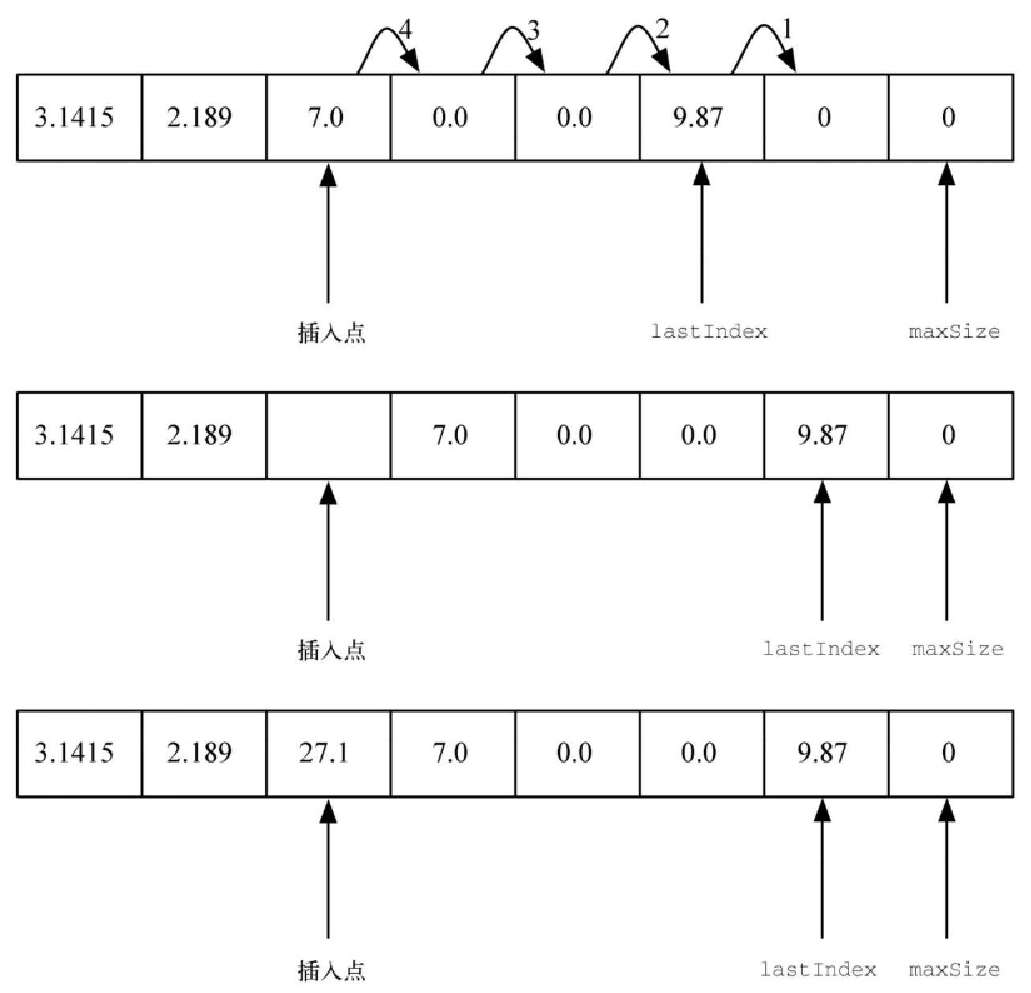
image 2023 12 14 10 54 50 942
Figure 2. 图8-2 往ArrayList中下标为2的位置插入元素27.1

正确实现 insert 的关键是，在移动数组中的元素时，不能覆盖任何重要数据。要做到这一点，应该从列表末尾开始复制数据。代码清单8-3 给出了 insert 方法的实现。注意第 4 行如何设置范围，以确保先将已有的数据复制到未使用的空间，然后才复制后续的值并覆盖已移走的值。如果 for 循环从插入点开始，将值往下一个位置复制，那么下一个位置上的旧值就再也找不回来了。

代码清单8-3 ArrayList类的insert方法
def insert(self, idx, val):
    if self.lastIndex > self.maxSize - 1:
        self.__resize()
    for i in range(self.lastIndex, idx - 1, -1):
        self.myArray[i + 1] = self.myArray[i]
    self.lastIndex += 1
    self.myArray[idx] = val

插入操作的时间复杂度是 \$O(n)\$，因为在最坏情况下，即在位置 0 处插入元素，需要将所有元素都挪一位。普通情况是只挪一半元素，但时间复杂度仍然是 \$O(n)\$。请回到第 3 章，复习如何使用 “节点与引用” 模式实现列表操作。实现没有对错之分，只不过不同的实现有着不同的性能。具体来说，是在表头加入元素，还是在表尾？是要从列表中删除元素，还是只往列表中添加元素？

对于 ArrayList，还有一些有趣的操作没有实现，包括 pop、del、index 以及让 ArrayList 支持迭代。对这些操作的实现留作练习。