复杂的递归问题

前几节探讨了一些容易用递归解决的问题，以及有助于理解递归的一些有趣的绘图问题。本节将探讨一些用循环难以解决却能用递归轻松解决的问题。最后会探讨一个颇具欺骗性的问题。它看上去可以用递归巧妙地解决，但是实际上并非如此。

汉诺塔

汉诺塔问题由法国数学家爱德华·卢卡斯于 1883 年提出。他的灵感是一个与印度寺庙有关的传说，相传这座寺庙里的年轻修行者试图解决这个难题。起初，修行者有3根柱子和 64 个依次叠好的金盘子，下面的盘子大，上面的盘子小。修行者的任务是将 64 个叠好的盘子从一根柱子移动到另一根柱子，同时有两个重要的限制条件：每次只能移动一个盘子，并且大盘子不能放在小盘子之上。修行者夜以继日地移动盘子（每一秒移动一个盘子），试图完成任务。根据传说，如果他们完成这项任务，整座寺庙将倒塌，整个世界也将消失。

尽管这个传说非常有意思，但是并不需要担心世界会因此而毁灭。要正确移动 64 个盘子，所需的步数是 264-1 = 18446744073709551615。根据每秒移动一次的速度，整个过程大约需要 584942417355年！显然，这个谜题并不像听上去那么简单。

图4-11 展示了一个例子，这是在将所有盘子从第一根柱子移到第三根柱子的过程中的一个中间状态。注意，根据前面说明的规则，每一根柱子上的盘子都是从下往上由大到小依次叠起来的。如果你之前从未求解过这个问题，不妨现在就试一下。不需要精致的盘子和柱子，一堆书或者一叠纸就足够了。

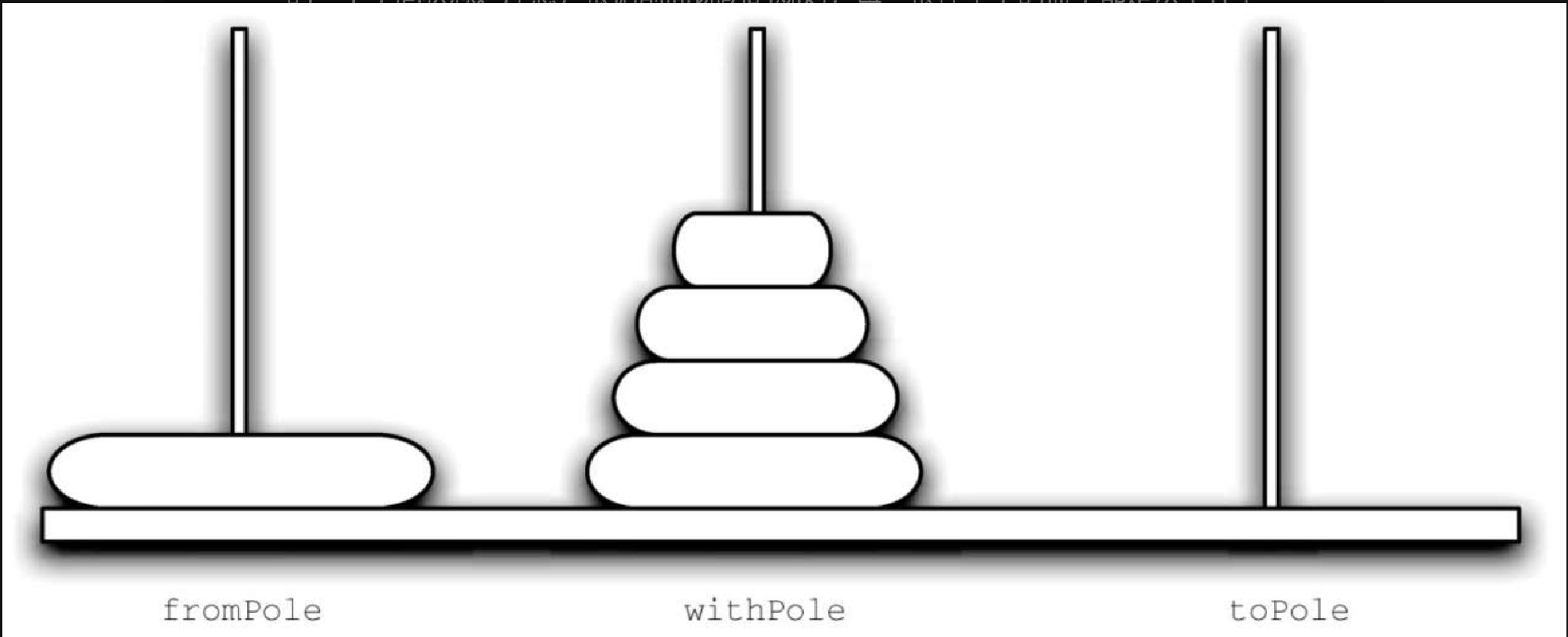
image 2023 12 13 11 24 52 488
Figure 1. 图4-11 汉诺塔问题示例

如何才能递归地解决这个问题呢？它真的可解吗？基本情况是什么？让我们自底向上地来考虑这个问题。假设第一根柱子起初有 5 个盘子。如果我们知道如何把上面 4 个盘子移动到第二根柱子上，那么就能轻易地把最底下的盘子移动到第三根柱子上，然后将 4 个盘子从第二根柱子移动到第三根柱子。但是如果不知道如何移动4个盘子，该怎么办呢？如果我们知道如何把上面 3 个盘子移动到第三根柱子上，那么就能轻易地把第 4 个盘子移动到第二根柱子上，然后再把 3 个盘子从第三根柱子移动到第二根柱子。但是如果不知道如何移动 3 个盘子，该怎么办呢？移动两个盘子到第二根柱子，然后把第 3 个盘子移动到第三根柱子，最后把之前的两个盘子移过来，怎么样？但是如果还是不知道如何移动两个盘子，该怎么办呢？你肯定会说，把一个盘子移动到第三根柱子并不难，甚至会说太简单。这看上去就是本例的基本情况。

以下概述如何借助一根中间柱子，将高度为 height 的一叠盘子从起点柱子移到终点柱子：

  1. 借助终点柱子，将高度为 height - 1 的一叠盘子移到中间柱子；

  2. 将最后一个盘子移到终点柱子；

  3. 借助起点柱子，将高度为 height - 1 的一叠盘子从中间柱子移到终点柱子。

只要总是遵守大盘子不能叠在小盘子之上的规则，就可以递归地执行上述步骤，就像最下面的大盘子不存在一样。上述步骤仅缺少对基本情况的判断。最简单的汉诺塔只有一个盘子。在这种情况下，只需将这个盘子移到终点柱子即可，这就是基本情况。此外，上述步骤通过逐渐减小高度 height 来向基本情况靠近。代码清单4-8 展示了解决汉诺塔问题的 Python 代码。

代码清单4-8 解决汉诺塔问题的Python代码
def moveTower(height,fromPole, toPole, withPole):
    if height >= 1:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(fromPole,toPole)
        moveTower(height-1,withPole,toPole,fromPole)

代码清单4-8 几乎和用英语描述一样。算法如此简洁的关键在于进行两个递归调用，分别在第 3 行和第 5 行。第 3 行将除了最后一个盘子以外的其他所有盘子从起点柱子移到中间柱子。第 4 行简单地将最后一个盘子移到终点柱子。第 5 行将之前的塔从中间柱子移到终点柱子，并将其放置在最大的盘子之上。基本情况是高度为 0。此时，不需要做任何事情，因此 moveTower 函数直接返回。这样处理基本情况时需要记住，从 moveTower 返回才能调用 moveDisk。

moveDisk 函数非常简单，如代码清单4-9 所示。它所做的就是打印出一条消息，说明将盘子从一根柱子移到另一根柱子。不妨尝试运行 moveTower 程序，你会发现它是非常高效的解决方案。

代码清单4-9 moveDisk函数
def moveDisk(fp,tp):
    print("moving disk from",fp,"to",tp)

看完 moveTower 和 moveDisk 的实现代码，你可能会疑惑为什么没有一个数据结构显式地保存柱子的状态。下面是一个提示：若要显式地保存柱子的状态，就需要用到 3 个 Stack 对象，一根柱子对应一个栈。Python 通过调用栈隐式地提供了我们所需的栈，就像在 toStr 的例子中一样。