术语及定义

顶点又称节点，是图的基础部分。它可以有自己的名字，我们称作 “键”。顶点也可以带有附加信息，我们称作 “有效载荷”。

边是图的另一个基础部分。两个顶点通过一条边相连，表示它们之间存在关系。边既可以是单向的，也可以是双向的。如果图中的所有边都是单向的，我们称之为有向图。图7-1 明显是一个有向图，因为必须修完某些课程后才能修后续的课程。

边可以带权重，用来表示从一个顶点到另一个顶点的成本。例如在路线图中，从一个城市到另一个城市，边的权重可以表示两个城市之间的距离。

有了上述定义之后，就可以正式地定义图。图可以用 G 来表示，并且 G = (V, E)。其中，V 是一个顶点集合，E 是一个边集合。每一条边是一个二元组 (v, w)，其中 w,v∈V。可以向边的二元组中再添加一个元素，用于表示权重。子图 s 是一个由边 e 和顶点 v 构成的集合，其中 e⊂E 且 v⊂V。

图7-2 展示了一个简单的带权有向图。我们可以用 6 个顶点和 9 条边的两个集合来正式地描述这个图：

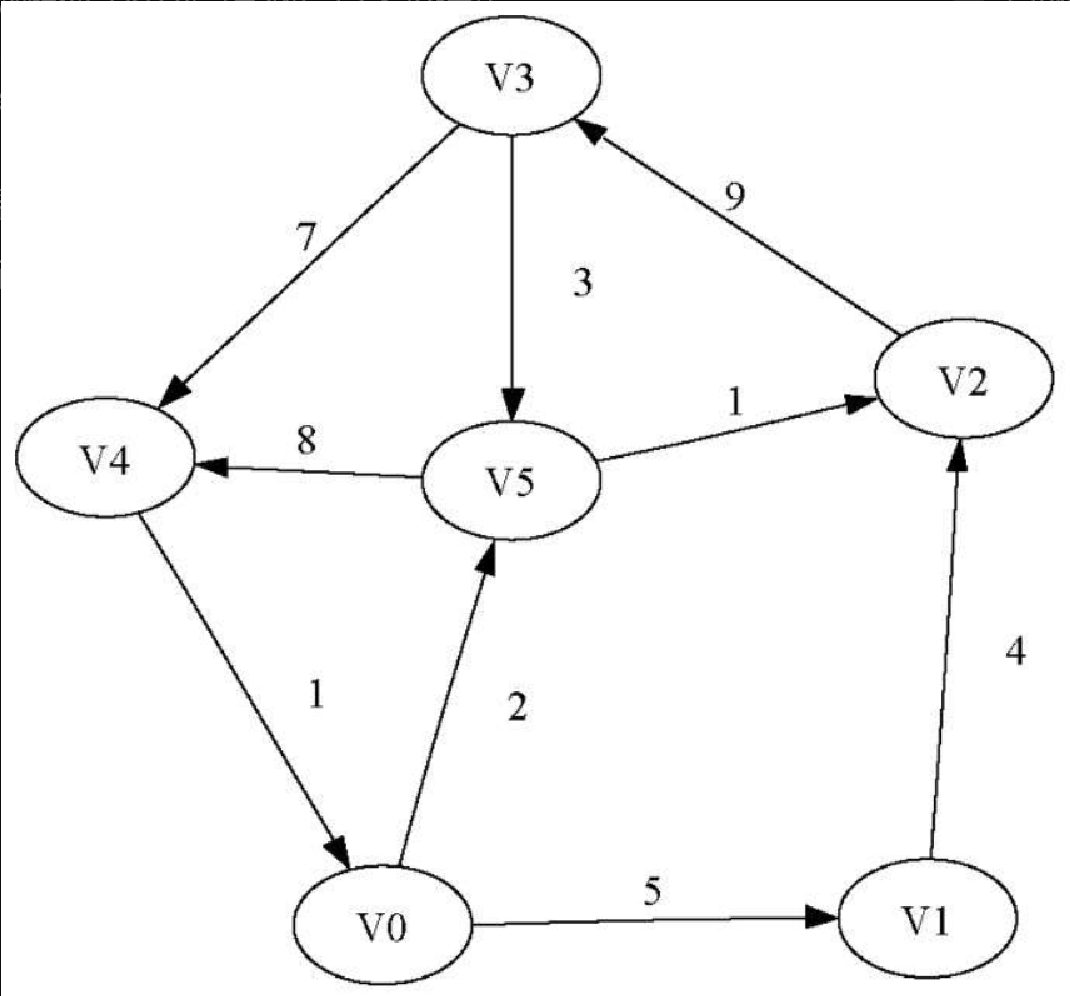Figure 1. 图7-2 简单的带权有向图

路径是由边连接的顶点组成的序列。路径的正式定义为 w1, w2, ···, wn，其中对于所有的 1≤i≤n-1，有 (wi, wi+1)∈E。无权重路径的长度是路径上的边数，有权重路径的长度是路径上的边的权重之和。以图7-2为例，从 V3 到 V1 的路径是顶点序列 (V 3, V 4, V 0, V1)，相应的边是 {(v3, v4,7), (v4, v0,1), (v0, v1,5)}。

环是有向图中的一条起点和终点为同一个顶点的路径。例如，图7-2中的路径 (V5,V2, V3, V5) 就是一个环。没有环的图被称为 无环图，没有环的有向图被称为有向无环图，简称为 DAG。接下来会看到，DAG 能帮助我们解决很多重要的问题。