栈

何谓栈

栈有时也被称作 “下推栈”。它是有序集合，添加操作和移除操作总发生在同一端，即 “顶端”，另一端则被称为 “底端”。

栈中的元素离底端越近，代表其在栈中的时间越长，因此栈的底端具有非常重要的意义。最新添加的元素将被最先移除。这种排序原则被称作 LIFO（last-in first-out），即后进先出。它提供了一种基于在集合中的时间来排序的方式。最近添加的元素靠近顶端，旧元素则靠近底端。

栈的例子在日常生活中比比皆是。几乎所有咖啡馆都有一个由托盘或盘子构成的栈，你可以从顶部取走一个，下一个顾客则会取走下面的托盘或盘子。图3-1 是由书构成的栈，唯一露出封面的书就是顶部的那本。为了拿到其他某本书，需要移除压在其上面的书。图3-2 展示了另一个栈，它包含一些原生的 Python 数据对象。

Figure 1. 图3-1 由书构成的栈

Figure 2. 图3-2 由原生的Python数据对象构成的栈

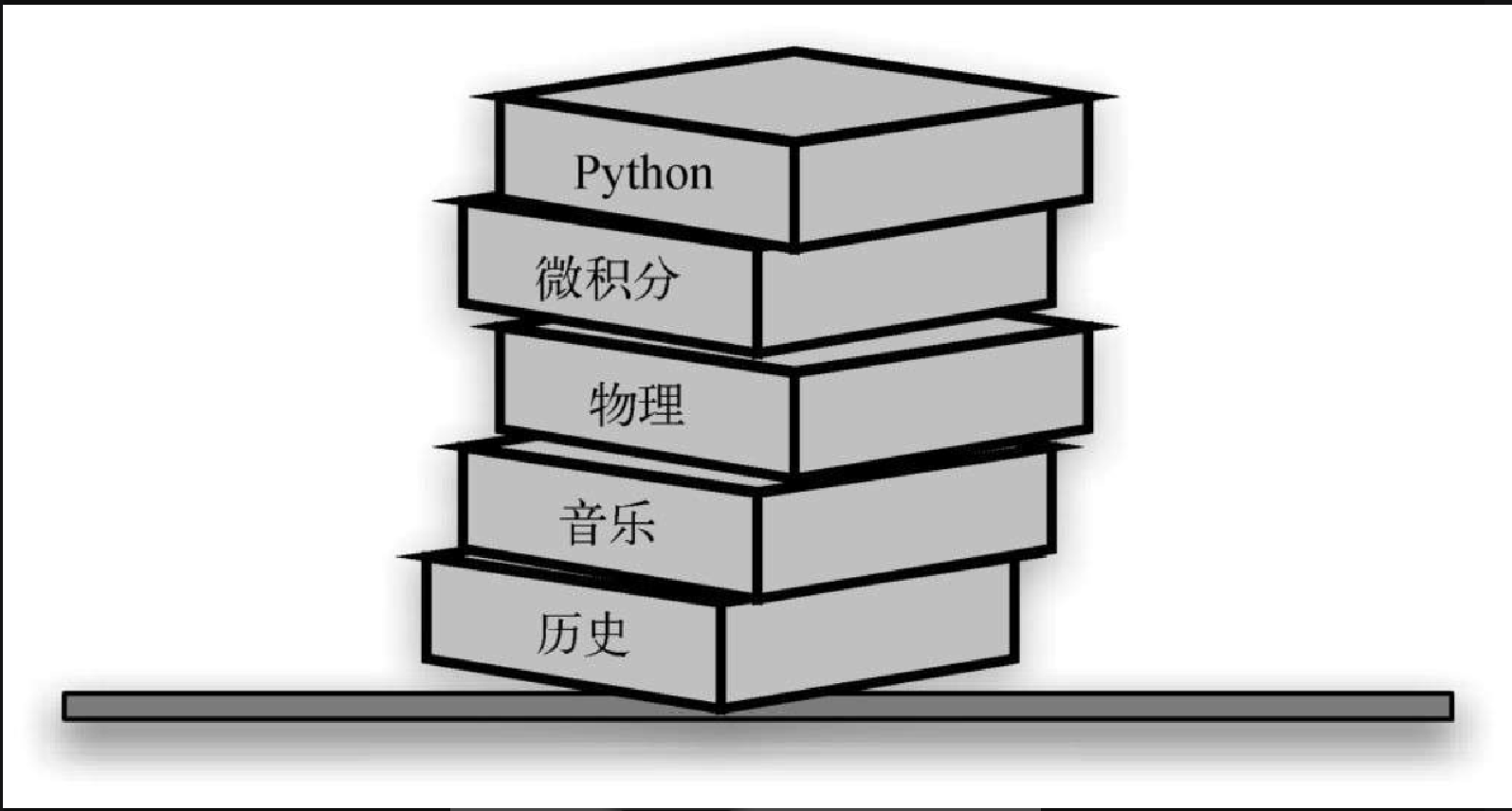
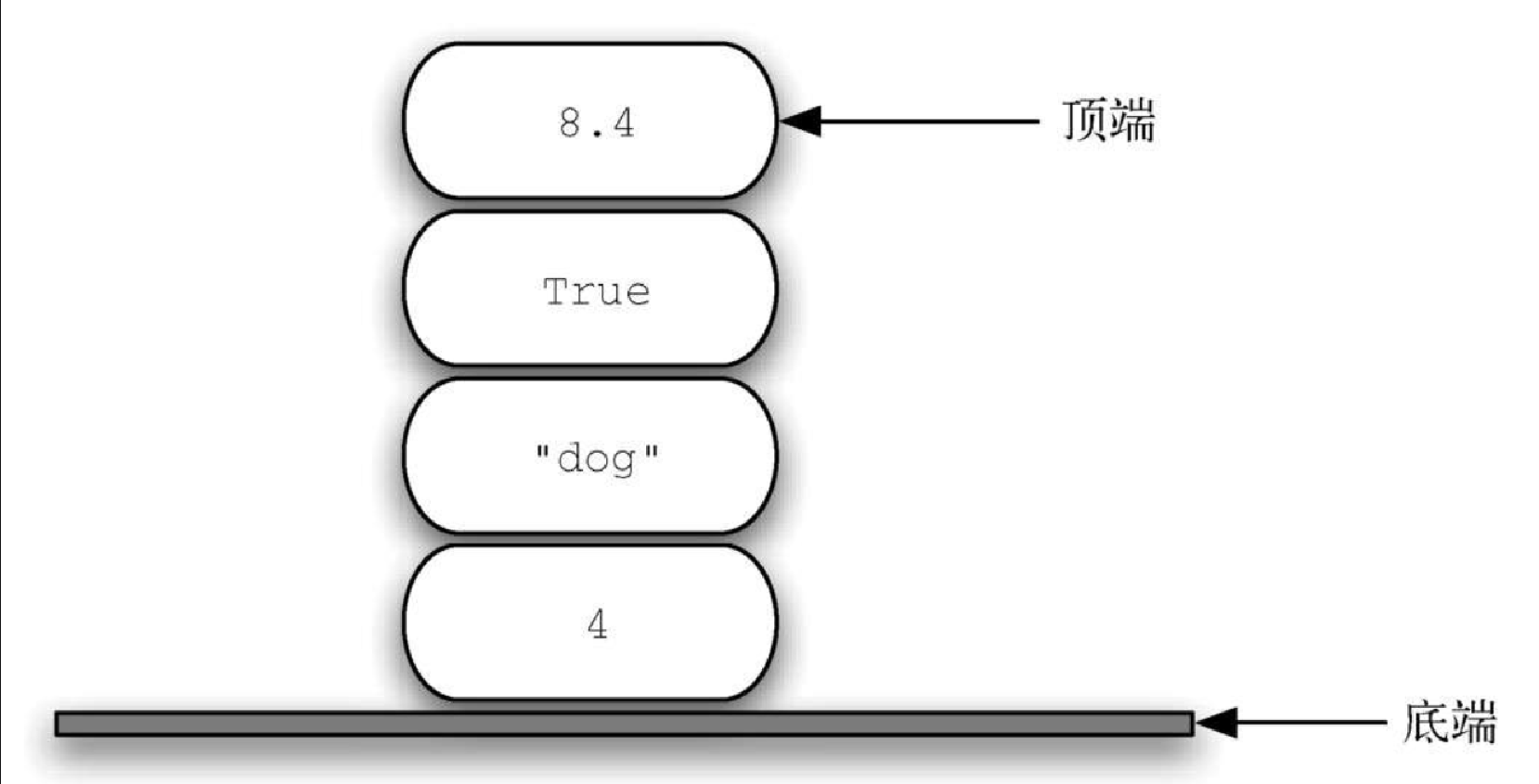
观察元素的添加顺序和移除顺序，就能理解栈的重要思想。假设桌面一开始是空的，每次只往桌上放一本书。如此堆叠，便能构建出一个栈。取书的顺序正好与放书的顺序相反。由于可用于反转元素的排列顺序，因此栈十分重要。元素的插入顺序正好与移除顺序相反。图3-3 展示了 Python 数据对象栈的创建过程和拆除过程。请仔细观察数据对象的顺序。

Figure 3. 图3-3 栈的反转特性

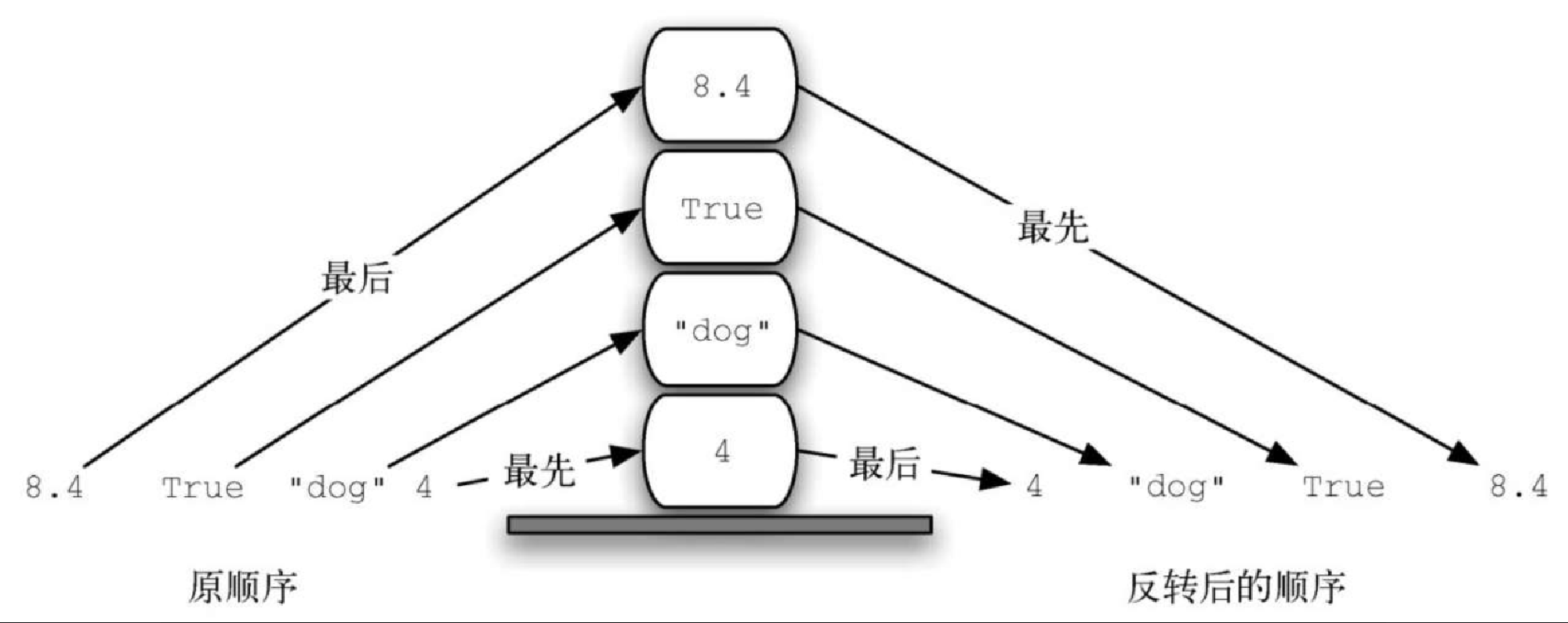
考虑到栈的反转特性，我们可以想到在使用计算机时的一些例子。例如，每一个浏览器都有返回按钮。当我们从一个网页跳转到另一个网页时，这些网页——实际上是URL——都被存放在一个栈中。当前正在浏览的网页位于栈的顶端，最早浏览的网页则位于底端。如果点击返回按钮，便开始反向浏览这些网页。

栈抽象数据类型

栈抽象数据类型由下面的结构和操作定义。如前所述，栈是元素的有序集合，添加操作与移除操作都发生在其顶端。栈的操作顺序是 LIFO，它支持以下操作。

Stack() 创建一个空栈。它不需要参数，且会返回一个空栈。
push(item) 将一个元素添加到栈的顶端。它需要一个参数 item，且无返回值。
pop() 将栈顶端的元素移除。它不需要参数，但会返回顶端的元素，并且修改栈的内容。
peek() 返回栈顶端的元素，但是并不移除该元素。它不需要参数，也不会修改栈的内容。
isEmpty() 检查栈是否为空。它不需要参数，且会返回一个布尔值。
size() 返回栈中元素的数目。它不需要参数，且会返回一个整数。

假设 s 是一个新创建的空栈。表3-1 展示了对 s 进行一系列操作的结果。在 “栈内容” 一列中，栈顶端的元素位于最右侧。

Figure 4. 表3-1 栈操作示例

用Python实现栈

明确定义栈抽象数据类型之后，我们开始用 Python 来将其实现。如前文所述，抽象数据类型的实现常被称为数据结构。正如第 1 章所述，和其他面向对象编程语言一样，每当需要在 Python 中实现像栈这样的抽象数据类型时，就可以创建新类。栈的操作通过方法实现。更进一步地说，因为栈是元素的集合，所以完全可以利用 Python 提供的强大、简单的原生集合来实现。这里，我们将使用列表。

Python 列表是有序集合，它提供了一整套方法。举例来说，对于列表 [2, 5, 3, 6, 7,4]，只需要考虑将它的哪一边视为栈的顶端。一旦确定了顶端，所有的操作就可以利用 append 和 pop 等列表方法来实现。

代码清单3-1 是栈的实现，它假设列表的尾部是栈的顶端。当栈增长时（即进行 push 操作），新的元素会被添加到列表的尾部。pop 操作同样会修改这一端。

代码清单3-1 用Python实现栈

class Stack:
     def __init__(self):
         self.items = []

     def isEmpty(self):
         return self.items == []

     def push(self, item):
         self.items.append(item)

     def pop(self):
         return self.items.pop()

     def peek(self):
         return self.items[len(self.items)-1]

     def size(self):
         return len(self.items)

以下展示了表3-1 中的栈操作及其返回结果。

>>> s = Stack()
>>> s.isEmpty()
True
>>> s.push(4)
>>> s.push('dog')
>>> s.peek()
'dog'
>>> s.push(True)
>>> s.size()
3
>>> s.isEmpty()
False
>>> s.push(8.4)
>>> s.pop()
8.4
>>> s.pop()
True
>>> s.size()
2

值得注意的是，也可以选择将列表的头部作为栈的顶端。不过在这种情况下，便无法直接使用 pop 方法和 append 方法，而必须要用 pop 方法和 insert 方法显式地访问下标为 0 的元素，即列表中的第 1 个元素。

代码清单3-2展示了这种实现。

class Stack:
    def __init__(self):
        self.items = []

    def isEmpty(self):
        return self.items == []

    def push(self, item):
        self.items.insert(0, item)

    def pop(self):
        return self.items.pop(0)

    def peek(self):
        return self.items[0]

    def size(self):
        return len(self.items)

s = Stack()
s.push('hello')
s.push('true')
print(s.pop())

改变抽象数据类型的实现却保留其逻辑特征，这种能力体现了抽象思想。不过，尽管上述两种实现都可行，但是二者在性能方面肯定有差异。append 方法和 pop() 方法的时间复杂度都是 \$O(1)\$，这意味着不论栈中有多少个元素，第一种实现中的 push 操作和 pop 操作都会在恒定的时间内完成。第二种实现的性能则受制于栈中的元素个数，这是因为 insert(0) 和 pop(0) 的时间复杂度都是 \$O(n)\$，元素越多就越慢。显而易见，尽管两种实现在逻辑上是相等的，但是它们在进行基准测试时耗费的时间会有很大的差异。

匹配括号

接下来，我们使用栈解决实际的计算机科学问题。我们都写过如下所示的算术表达式。

(5 + 6) * (7 + 8) / (4 + 3)

其中的括号用来改变计算顺序。像 Lisp 这样的编程语言有如下语法结构。

(defun square(n)
        (* n n))

它定义了一个名为 square 的函数，该函数会返回参数 n 的平方值。Lisp 所用括号之多，令人咋舌。

在以上两个例子中，括号都前后匹配。匹配括号是指每一个左括号都有与之对应的一个右括号，并且括号对有正确的嵌套关系。下面是正确匹配的括号串。

(()()()())
(((())))
(()((())()))

下面的这些括号则是不匹配的。

((((((())
()))
(()()(()

能够分辨括号匹配得正确与否，对于识别编程语言的结构来说非常重要。

我们的挑战就是编写一个算法，它从左到右读取一个括号串，然后判断其中的括号是否匹配。为了解决这个问题，需要注意到一个重要现象。当从左到右处理括号时，最右边的无匹配左括号必须与接下来遇到的第一个右括号相匹配，如图3-4 所示。并且，在第一个位置的左括号可能要等到处理至最后一个位置的右括号时才能完成匹配。相匹配的右括号与左括号出现的顺序相反。这一规律暗示着能够运用栈来解决括号匹配问题。

Figure 5. 图3-4 匹配括号

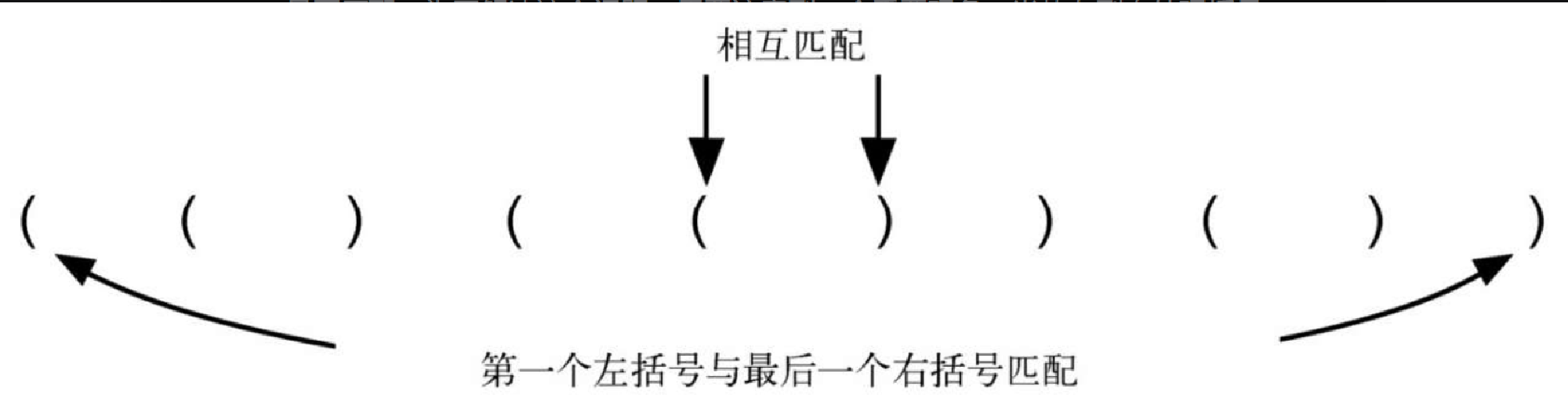
一旦认识到用栈来保存括号是合理的，算法编写起来就会十分容易。由一个空栈开始，从左往右依次处理括号。如果遇到左括号，便通过 push 操作将其加入栈中，以此表示稍后需要有一个与之匹配的右括号。反之，如果遇到右括号，就调用 pop 操作。只要栈中的所有左括号都能遇到与之匹配的右括号，那么整个括号串就是匹配的；如果栈中有任何一个左括号找不到与之匹配的右括号，则括号串就是不匹配的。在处理完匹配的括号串之后，栈应该是空的。代码清单3-3 展示了实现这一算法的 Python 代码。

代码清单3-3 匹配括号

from pythonds.basic import Stack

def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == "(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                s.pop()

        index = index + 1

    if balanced and s.isEmpty():
        return True
    else:
        return False

print(parChecker('((()))'))
print(parChecker('(()'))

parChecker 函数假设 Stack 类可用，并且会返回一个布尔值来表示括号串是否匹配。注意，布尔型变量 balanced 的初始值是 True，这是因为一开始没有任何理由假设其为 False。如果当前的符号是左括号，它就会被压入栈中（第9～10行）。注意第 15 行，仅通过 pop() 将一个元素从栈中移除。由于移除的元素一定是之前遇到的左括号，因此并没有用到 pop() 的返回值。在第19～22行，只要所有括号匹配并且栈为空，函数就会返回 True，否则返回 False。

普通情况：匹配符号

符号匹配是许多编程语言中的常见问题，括号匹配问题只是一个特例。匹配符号是指正确地匹配和嵌套左右对应的符号。例如，在 Python 中，方括号 [ 和 ] 用于列表；花括号 { 和 } 用于字典；括号 ( 和 ) 用于元组和算术表达式。只要保证左右符号匹配，就可以混用这些符号。以下符号串是匹配的，其中不仅每一个左符号都有一个右符号与之对应，而且两个符号的类型也是一致的。

{{([][])}()}
[[{{(())}}]]
[][][](){}

以下符号串则是不匹配的。

([)]
((()]))
[{()]

要处理新类型的符号，可以轻松扩展 3.3.4 节中的括号匹配检测器。每一个左符号都将被压入栈中，以待之后出现对应的右符号。唯一的区别在于，当出现右符号时，必须检测其类型是否与栈顶的左符号类型相匹配。如果两个符号不匹配，那么整个符号串也就不匹配。同样，如果整个符号串处理完成并且栈是空的，那么就说明所有符号正确匹配。

代码清单3-4 展示了实现上述算法的 Python 程序。唯一的改动在第 17 行，我们调用了一个辅助函数来匹配符号。必须检测每一个从栈顶移除的符号是否与当前的右符号相匹配。如果不匹配，布尔型变量 balanced 就被设成 False。

代码清单3-4 匹配符号

from pythonds.basic import Stack

def parChecker(symbolString):
    s = Stack()

    balanced = True
    index = 0

    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol in "([{":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                top = s.pop()
                if not matches(top,symbol):
                       balanced = False

        index = index + 1

    if balanced and s.isEmpty():
        return True
    else:
        return False

def matches(open,close):
    opens = "([{"
    closers = ")]}"
    return opens.index(open) == closers.index(close)


print(parChecker('{({([][])}())}'))
print(parChecker('[{()]'))

以上两个例子说明，在处理编程语言的语法结构时，栈是十分重要的数据结构。几乎所有记法都有某种需要正确匹配和嵌套的符号。除此之外，栈在计算机科学中还有其他一些重要的应用场景，让我们继续探索。

将十进制数转换成二进制数

在学习计算机科学的过程中，我们基本上都接触过二进制数。由于所有存储在计算机中的值都是由 0 和 1 组成的字符串，因此二进制在计算机科学中非常重要。如果不能在二进制表达方式和常见表达方式之间转换，我们与计算机的交互就会非常麻烦。

整数是常见的数据项，它们在计算机程序中无处不在。我们在数学课上学习过整数，并且会用十进制或者以 10 为基来表示它们。十进制数 233₁₀ 及其对应的二进制数 11101001₂ 可以分别按下面的形式表示。

\$2×10^2+3×10^1+3×10^0\$

\$1×2^7+1×2^6+1×2^5+0×2^4+1×2^3+0×2^2+0×2^1+1×2^0\$

如何才能简便地将整数值转换成二进制数呢？答案是利用一种叫作 “除以2” 的算法，该算法使用栈来保存二进制结果的每一位。

“除以2” 算法假设待处理的整数大于0。它用一个简单的循环不停地将十进制数除以 2，并且记录余数。第一次除以 2 的结果能够用于区分偶数和奇数。如果是偶数，则余数为 0，因此个位上的数字为 0；如果是奇数，则余数为 1，因此个位上的数字为 1。可以将要构建的二进制数看成一系列数字；计算出的第一个余数是最后一位。如图 3-5 所示，这又一次体现了反转特性，因此用栈来解决该问题是合理的。

Figure 6. 图3-5 将十进制数转换成二进制数

代码清单3-5 展示了 “除以2” 算法的 Python 实现。divideBy2 函数接受一个十进制数作为参数，然后不停地将其除以 2。第 6 行使用了内建的取余运算符 %，第 7 行将求得的余数压入栈中。当除法过程遇到 0 之后，第 10～12 行就会构建一个二进制数字串。第 10 行创建一个空串。随后，二进制数字从栈中被逐个取出，并添加到数字串的最右边。最后，函数返回该二进制数字串。

代码清单3-5 “除以2” 算法的 Python 实现

from pythonds.basic import Stack

def divideBy2(decNumber):
    remstack = Stack()

    while decNumber > 0:
        rem = decNumber % 2
        remstack.push(rem)
        decNumber = decNumber // 2

    binString = ""
    while not remstack.isEmpty():
        binString = binString + str(remstack.pop())

    return binString

print(divideBy2(42))

这个将十进制数转换成二进制数的算法很容易扩展成对任何进制的转换。在计算机科学中，常常使用不同编码的数字，其中最常见的是二进制、八进制和十六进制。

十进制数 233₁₀ 对应的八进制数 351₈ 和十六进制数 E9₁₆ 可以分别按下面的形式表示。

\$3×8^2+5×8^1+1×8^0\$

\$15×16^1+9×16^0\$

可以将 divideBy2 函数修改成接受一个十进制数以及希望转换的进制基数，“除以2” 则变成 “除以基数”。在代码清单3-6 中，baseConverter 函数接受一个十进制数和一个 2～16 的基数作为参数。处理方法仍然是将余数压入栈中，直到被处理的值为 0。之前的从左到右构建数字串的方法只需要修改一处。以 2～10 为基数时，最多只需要 10 个数字，因此 0～9 这 10 个整数够用。当基数超过 10 时，就会遇到问题。不能再直接使用余数，这是因为余数本身就是两位的十进制数。因此，需要创建一套数字来表示大于 9 的余数。

一种解决方法是添加一些字母字符到数字中。例如，十六进制使用 10 个数字以及前 6 个字母来代表 16 位数字。在代码清单3-6 中，为了实现这一方法，第 3 行创建了一个数字字符串来存储对应位置上的数字。0 在位置 0,1 在位置 1, A 在位置 10, B 在位置 11，依此类推。当从栈中移除一个余数时，它可以被用作访问数字的下标，对应的数字会被添加到结果中。如果从栈中移除的余数是 13，那么字母 D 将被添加到结果字符串的最后。

代码清单3-6 将十进制数转换成任意进制数

from pythonds.basic import Stack

def baseConverter(decNumber,base):
    digits = "0123456789ABCDEF"

    remstack = Stack()

    while decNumber > 0:
        rem = decNumber % base
        remstack.push(rem)
        decNumber = decNumber // base

    newString = ""
    while not remstack.isEmpty():
        newString = newString + digits[remstack.pop()]

    return newString

print(baseConverter(25,2))
print(baseConverter(25,16))

前序、中序和后序表达式

对于像 B*C 这样的算术表达式，可以根据其形式来正确地运算。在 B*C 的例子中，由于乘号 * 出现在两个变量之间，因此我们知道应该用变量 B 乘以变量 C。因为运算符出现在两个操作数的中间，所以这种表达式被称作中序表达式。

来看另一个中序表达式的例子：A + B * C。虽然运算符 + 和 * 都在操作数之间，但是存在一个问题：它们分别作用于哪些操作数？ + 是否作用于 A 和 B ? * 是否作用于 B 和 C ？这个表达式看起来存在歧义。

事实上，我们经常读写这类表达式，并且没有遇到任何问题。这是因为，我们知道 + 和 * 的特点。每一个运算符都有一个优先级。在运算时，高优先级的运算符先于低优先级的运算符。唯一能够改变运算顺序的就是括号。乘法和除法的优先级高于加法和减法。如果两个运算符的优先级相同，那就按照从左到右或者结合性的顺序运算。

让我们从运算符优先级的角度来理解 A + B * C。首先计算 B * C，然后再将 A 与该乘积相加。(A + B) * C 则是先计算 A 与 B 之和，然后再进行乘法运算。在表达式 A + B + C 中，根据优先级法则（或者结合性），最左边的 + 会首先参与运算。

尽管这些规律对于人来说显而易见，计算机却需要明确地知道以何种顺序进行何种运算。一种杜绝歧义的写法是完全括号表达式。这种表达式对每一个运算符都添加一对括号。由括号决定运算顺序，没有任何歧义，并且不必记忆任何优先级规则。

A + B * C + D 可以被重写成 A + (B * C + D)，以表明乘法优先，然后计算左边的加法表达式。由于加法运算从左往右结合，因此 A + B + C + D 可以被重写成 (((A + B) +C) + D) 。

还有另外两种重要的表达式，也许并不能一目了然地看出它们的含义。考虑中序表达式 A + B。如果把运算符放到两个操作数之前，就得到 + A B。同理，如果把运算符移到最后，会得到 A B +。这两种表达式看起来有点奇怪。

通过改变运算符与操作数的相对位置，我们分别得到前序表达式和后序表达式。前序表达式要求所有的运算符出现在它所作用的两个操作数之前，后序表达式则相反。表3-2 列出了一些例子。

Figure 7. 表3-2 中序、前序与后序表达式

A + B * C 可以被重写为前序表达式 + A * B C。乘号出现在 B 和 C 之前，代表着它的优先级高于加号。加号出现在 A 和乘法结果之前。A + B * C 对应的后序表达式是 A B C * +。运算顺序仍然得以正确保留，这是由于乘号紧跟 B 和 C 出现，意味着它的优先级比加号更高。尽管运算符被移到了操作数的前面或者后面，但是运算顺序并没有改变。

现在来看看中序表达式 (A + B) * C。括号用来保证加号的优先级高于乘号。但是，当 A + B 被写成前序表达式时，只需将加号移到操作数之前，即 + A B。于是，加法结果就成了乘号的第一个操作数。乘号被移到整个表达式的最前面，从而得到 *+ A B C。同理，后序表达式 A B + 保证优先计算加法。乘法则在得到加法结果之后再计算。因此，正确的后序表达式为 A B + C *。

表3-3 列出了上述3个表达式。请注意一个非常重要的变化。在后两个表达式中，括号去哪里了？为什么前序表达式和后序表达式不需要括号？答案是，这两种表达式中的运算符所对应的操作数是明确的。只有中序表达式需要额外的符号来消除歧义。前序表达式和后序表达式的运算顺序完全由运算符的位置决定。鉴于此，中序表达式是最不理想的算式表达法。

Figure 8. 表3-3 括号的变化

表3-4 展示了更多的中序表达式及其对应的前序表达式和后序表达式。请确保自己明白对应的表达式为何在运算顺序上是等价的。

Figure 9. 表3-4 中序、前序与后序表达式示例

从中序向前序和后序转换

到目前为止，我们使用了特定的方法来将中序表达式转换成对应的前序表达式和后序表达式。正如你所想，存在通用的算法，可用于正确转换任意复杂度的表达式。

首先使用完全括号表达式。如前所述，可以将 A + B * C 写作 (A + (B * C))，以表示乘号的优先级高于加号。进一步观察后会发现，每一对括号其实对应着一个中序表达式（包含两个操作数以及其间的运算符）。

观察子表达式 (B * C) 的右括号。如果将乘号移到右括号所在的位置，并且去掉左括号，就会得到 B C *，这实际上是将该子表达式转换成了对应的后序表达式。如果把加号也移到对应的右括号所在的位置，并且去掉对应的左括号，就能得到完整的后序表达式，如图3-6 所示。

Figure 10. 图3-6 向右移动运算符，以得到后序表达式

如果将运算符移到左括号所在的位置，并且去掉对应的右括号，就能得到前序表达式，如图3-7 所示。实际上，括号对的位置就是其包含的运算符的最终位置。

Figure 11. 图3-7 向左移动运算符，以得到前序表达式

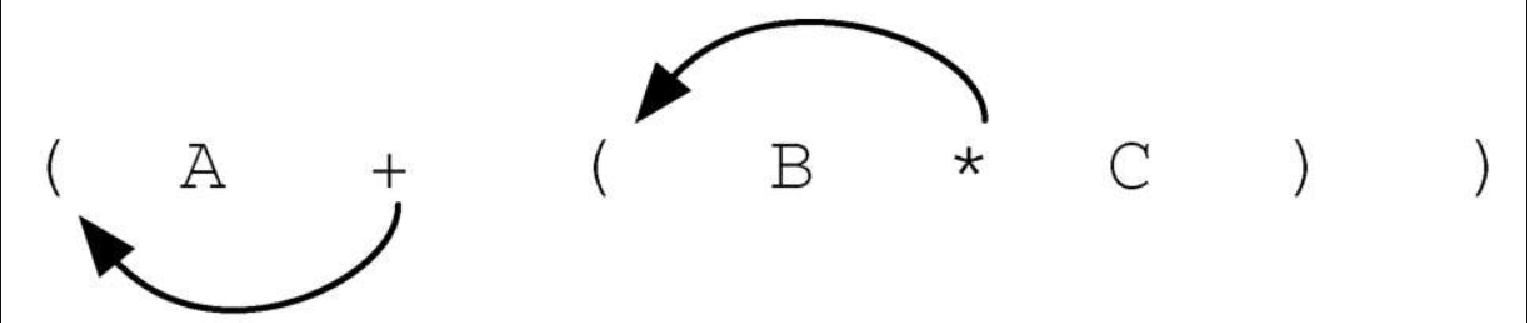
因此，若要将任意复杂的中序表达式转换成前序表达式或后序表达式，可以先将其写作完全括号表达式，然后将括号内的运算符移到左括号处（前序表达式）或者右括号处（后序表达式）。

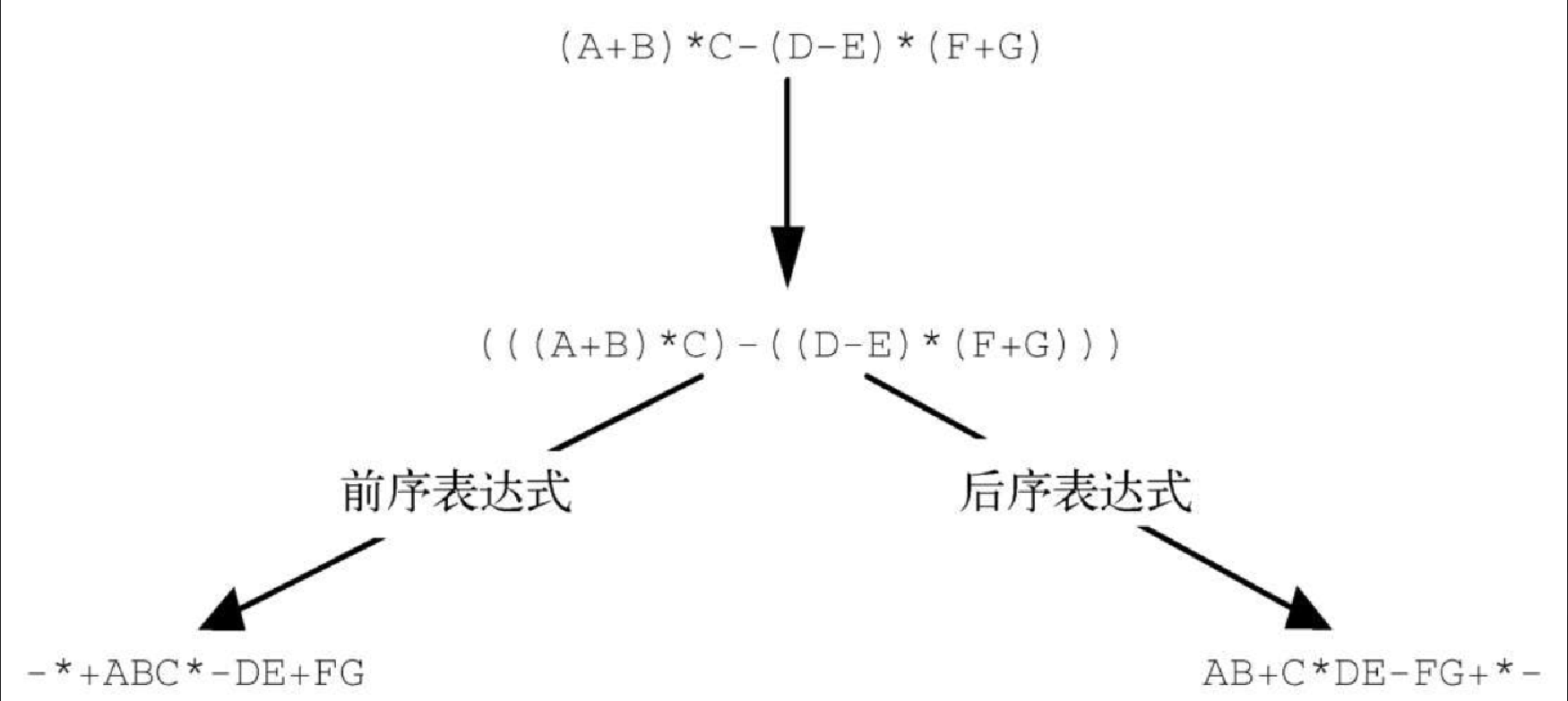
下面来看一个更复杂的表达式：(A + B) * C - (D - E) * (F + G)。图3-8 展示了将其转换成前序表达式和后序表达式的过程。

Figure 12. 图3-8 将复杂的中序表达式转换成前序表达式和后序表达式

从中序到后序的通用转换法

我们需要开发一种将任意中序表达式转换成后序表达式的算法。为了完成这个目标，让我们进一步观察转换过程。

再一次研究 A + B * C 这个例子。如前所示，其对应的后序表达式为 A B C *+。操作数 A、B 和 C 的相对位置保持不变，只有运算符改变了位置。再观察中序表达式中的运算符。从左往右看，第一个出现的运算符是 +。但是在后序表达式中，由于 的优先级更高，因此 先于 + 出现。在本例中，中序表达式的运算符顺序与后序表达式的相反。

在转换过程中，由于运算符右边的操作数还未出现，因此需要将运算符保存在某处。同时，由于运算符有不同的优先级，因此可能需要反转它们的保存顺序。本例中的加号与乘号就是这种情况。由于中序表达式中的加号先于优先级更高的乘号出现，因此后序表达式需要反转它们的出现顺序。鉴于这种反转特性，使用栈来保存运算符就显得十分合理。

对于 (A + B) * C，情况会如何呢？它对应的后序表达式为 A B + C *。从左往右看，首先出现的运算符是 +。不过，由于括号改变了运算符的优先级，因此当处理到 * 时，+ 已经被放入结果表达式中了。现在可以来总结转换算法：当遇到左括号时，需要将其保存，以表示接下来会遇到高优先级的运算符；那个运算符需要等到对应的右括号出现才能确定其位置（回忆一下完全括号表达式的转换法）；当右括号出现时，便可以将运算符从栈中取出来。

在从左往右扫描中序表达式时，我们利用栈来保存运算符。这样做可以提供反转特性。栈的顶端永远是最新添加的运算符。每当遇到一个新的运算符时，都需要对比它与栈中运算符的优先级。

假设中序表达式是一个以空格分隔的标记串。其中，运算符标记有 *、/、+ 和-，括号标记有(和)，操作数标记有 A、B、C 等。下面的步骤会生成一个后序标记串。

创建用于保存运算符的空栈 opstack，以及一个用于保存结果的空列表。
使用字符串方法 split 将输入的中序表达式转换成一个列表。
从左往右扫描这个标记列表。
- 如果标记是操作数，将其添加到结果列表的末尾。
- 如果标记是左括号，将其压入 opstack 栈中。
- 如果标记是右括号，反复从 opstack 栈中移除元素，直到移除对应的左括号。将从栈中取出的每一个运算符都添加到结果列表的末尾。
- 如果标记是运算符，将其压入 opstack 栈中。但是，在这之前，需要先从栈中取出优先级更高或相同的运算符，并将它们添加到结果列表的末尾。
当处理完输入表达式以后，检查 opstack。将其中所有残留的运算符全部添加到结果列表的末尾。

图3-9 展示了利用上述算法转换 A * B + C * D 的过程。注意，第一个 * 在处理至 + 时被移出栈。由于乘号的优先级高于加号，因此当第二个 * 出现时，+ 仍然留在栈中。在中序表达式的最后，进行了两次出栈操作，用于移除两个运算符，并将 + 放在后序表达式的末尾。

Figure 13. 图3-9 将中序表达式 A * B + C * D 转换为后序表达式 A B * C D * +

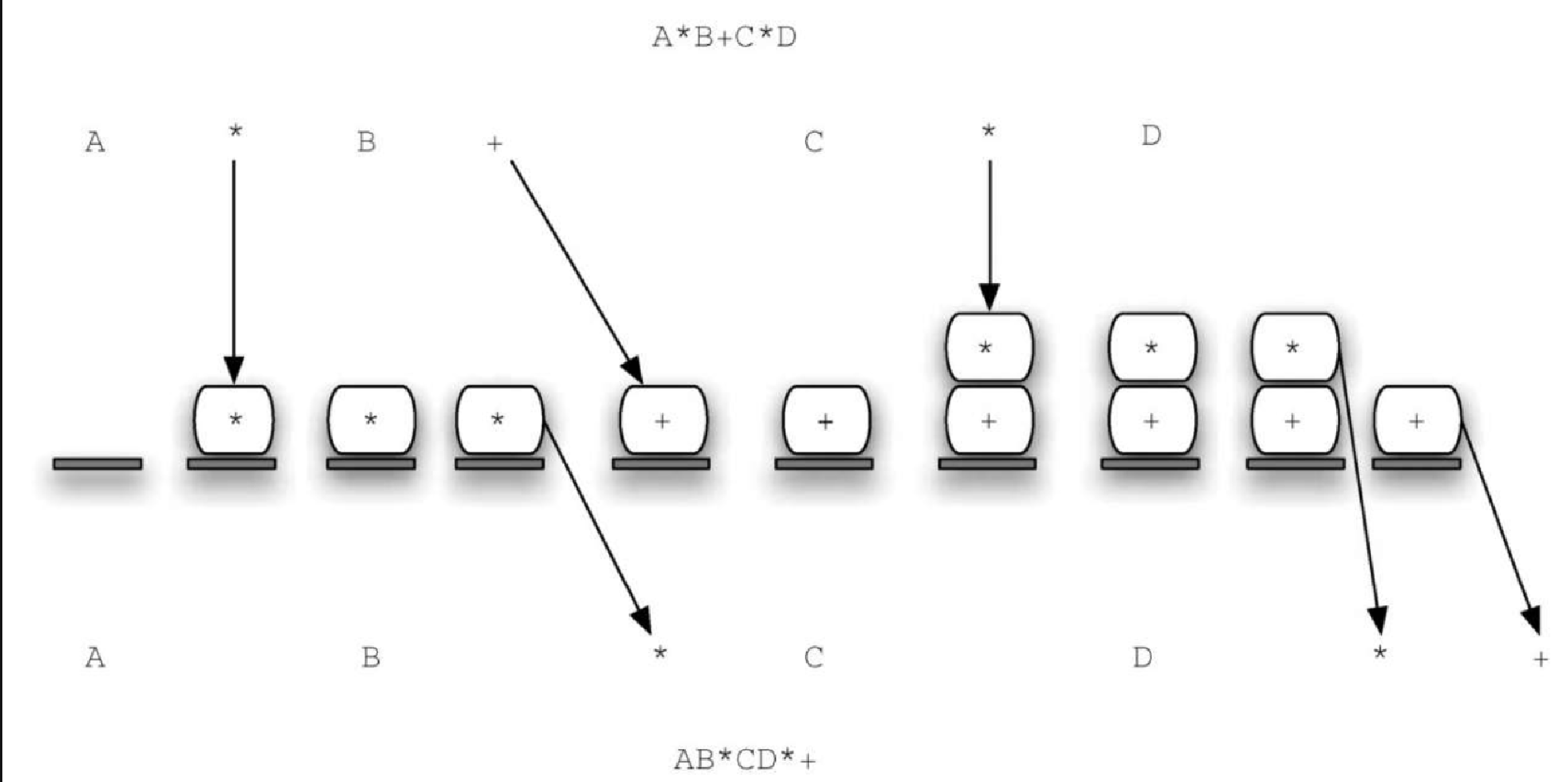
为了在 Python 中实现这一算法，我们使用一个叫作 prec 的字典来保存运算符的优先级值。该字典把每一个运算符都映射成一个整数。通过比较对应的整数，可以确定运算符的优先级（本例随意地使用了 3、2、1）。左括号的优先级值最小。这样一来，任何与左括号比较的运算符都会被压入栈中。我们也将导入 string 模块，它包含一系列预定义变量。本例使用一个包含所有大写字母的字符串（string.ascii_uppercase）来代表所有可能出现的操作数。代码清单 3-7 展示了完整的转换函数。

代码清单3-7 用Python实现从中序表达式到后序表达式的转换

from pythonds.basic import Stack

def infixToPostfix(infixexpr):
    prec = {}
    prec["*"] = 3
    prec["/"] = 3
    prec["+"] = 2
    prec["-"] = 2
    prec["("] = 1
    opStack = Stack()
    postfixList = []
    tokenList = infixexpr.split()

    for token in tokenList:
        if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
            postfixList.append(token)
        elif token == '(':
            opStack.push(token)
        elif token == ')':
            topToken = opStack.pop()
            while topToken != '(':
                postfixList.append(topToken)
                topToken = opStack.pop()
        else:
            while (not opStack.isEmpty()) and \
               (prec[opStack.peek()] >= prec[token]):
                  postfixList.append(opStack.pop())
            opStack.push(token)

    while not opStack.isEmpty():
        postfixList.append(opStack.pop())
    return " ".join(postfixList)

print(infixToPostfix("A * B + C * D"))
print(infixToPostfix("( A + B ) * C - ( D - E ) * ( F + G )"))

以下是一些例子的执行结果。

>>> infixtopostfix("( A + B ) * ( C + D )")
'A B + C D + *'
>>> infixtopostfix("( A + B ) * C")
'A B + C *'
>>> infixtopostfix("A + B * C")
'A B C * +'

计算后序表达式

最后一个关于栈的例子是计算后序表达式。在这个例子中，栈再一次成为适合选择的数据结构。不过，当扫描后序表达式时，需要保存操作数，而不是运算符。换一个角度来说，当遇到一个运算符时，需要用离它最近的两个操作数来计算。

为了进一步理解该算法，考虑后序表达式 45 6 *+。当从左往右扫描该表达式时，首先会遇到操作数 4 和 5。在遇到下一个符号之前，我们并不确定要对它们进行什么运算。将它们都保存在栈中，便可以在需要时取用。

在本例中，紧接着出现的符号又是一个操作数。因此，将 6 也压入栈中，并继续检查后面的符号。现在遇到运算符 *，这意味着需要将最近遇到的两个操作数相乘。通过执行两次出栈操作，可以得到相应的操作数，然后进行乘法运算（本例的结果是 30）。

接着，将结果压入栈中。这样一来，当遇到后面的运算符时，它就可以作为操作数。当处理完最后一个运算符之后，栈中只剩一个值。将这个值取出来，并作为表达式的结果返回。图3-10 展示了栈的内容在整个计算过程中的变化。

Figure 14. 图3-10 栈的内容在整个计算过程中的变化

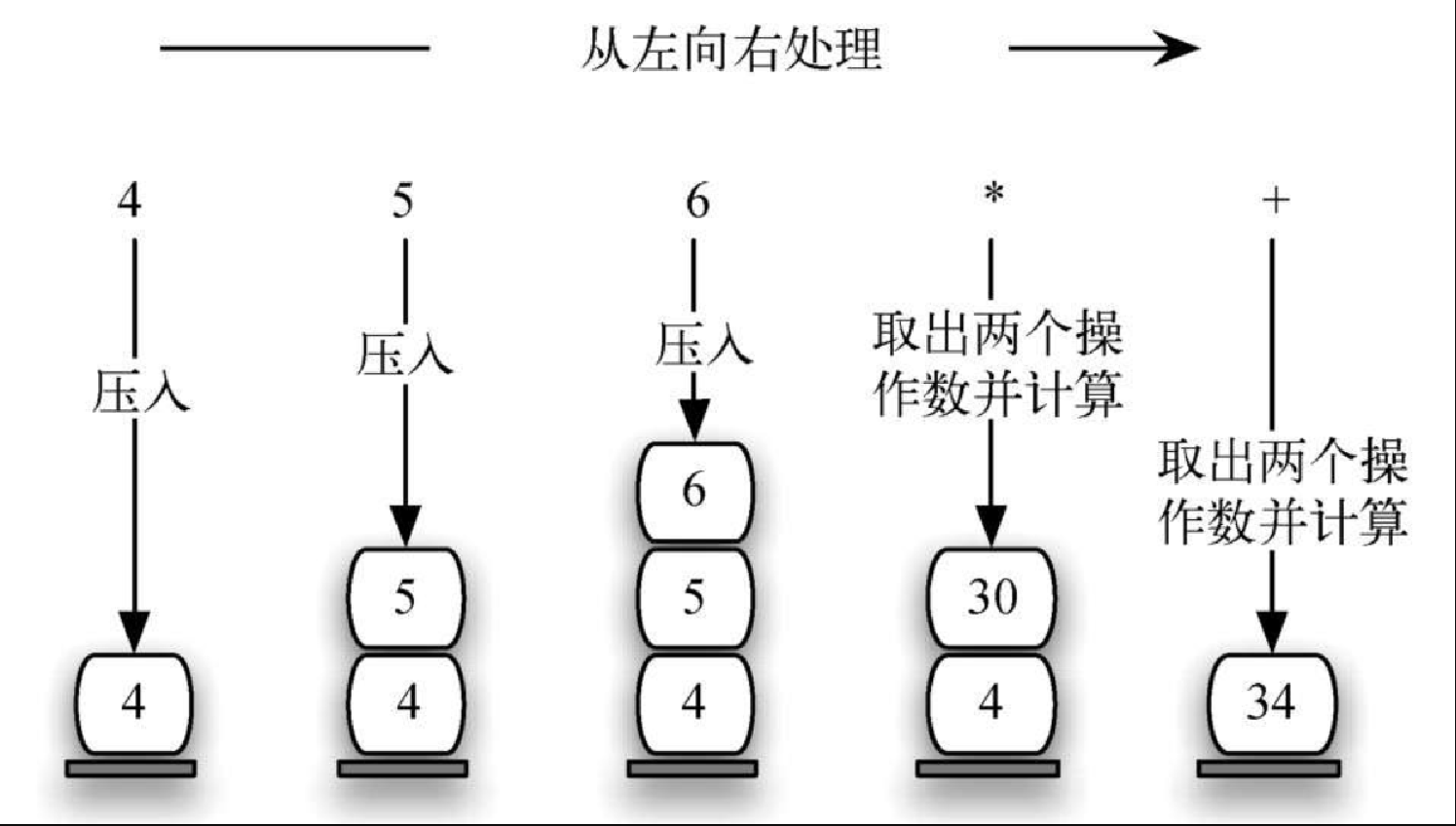
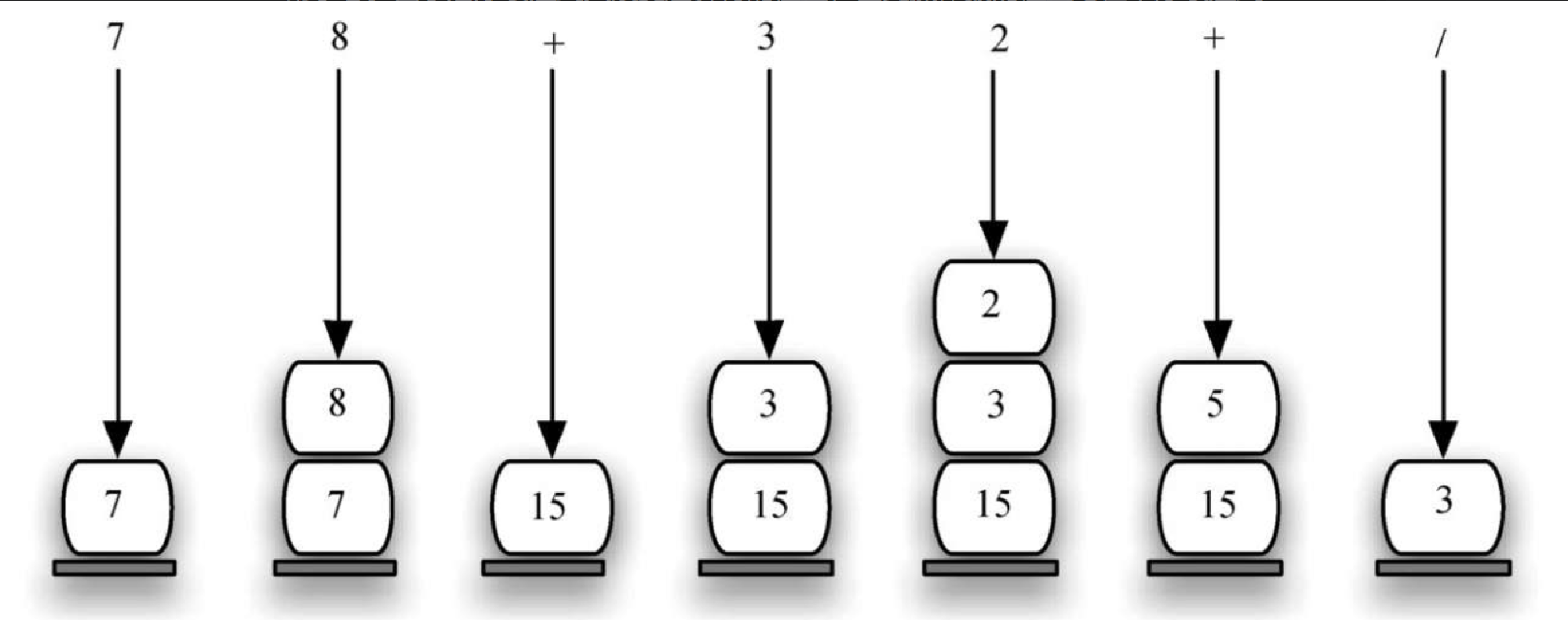
图3-11 展示了一个更复杂的例子：78 + 32 + /。有两处需要注意。首先，伴随着子表达式的计算，栈增大、缩小，然后再一次增大。其次，处理除法运算时需要非常小心。由于后序表达式只改变运算符的位置，因此操作数的位置与在中序表达式中的位置相同。当从栈中取出除号的操作数时，它们的顺序颠倒了。由于除号不是可交换的运算符（15/5 和 5/15 的结果不相同），因此必须保证操作数的顺序没有颠倒。

Figure 15. 图3-11 一个更复杂的例子

假设后序表达式是一个以空格分隔的标记串。其中，运算符标记有 *、/、+ 和 -，操作数标记是一位的整数值。结果是一个整数。

创建空栈 operandStack。
使用字符串方法 split 将输入的后序表达式转换成一个列表。
从左往右扫描这个标记列表。
- 如果标记是操作数，将其转换成整数并且压入 operandStack 栈中。
- 如果标记是运算符，从 operandStack 栈中取出两个操作数。第一次取出右操作数，第二次取出左操作数。进行相应的算术运算，然后将运算结果压入 operandStack 栈中。
当处理完输入表达式时，栈中的值就是结果。将其从栈中返回。

代码清单3-8 是计算后序表达式的完整函数。为了方便运算，我们定义了辅助函数 doMath。它接受一个运算符和两个操作数，并进行相应的运算。

代码清单3-8 用Python实现后序表达式的计算

from pythonds.basic import Stack

def postfixEval(postfixExpr):
    operandStack = Stack()
    tokenList = postfixExpr.split()

    for token in tokenList:
        if token in "0123456789":
            operandStack.push(int(token))
        else:
            operand2 = operandStack.pop()
            operand1 = operandStack.pop()
            result = doMath(token,operand1,operand2)
            operandStack.push(result)
    return operandStack.pop()

def doMath(op, op1, op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2

print(postfixEval('7 8 + 3 2 + /'))

需要注意的是，在后序表达式的转换和计算中，我们都假设输入表达式没有错误。在以上两个程序的基础上，添加错误检测和报告功能并不难。本章最后将此作为一个编程练习。