术语及定义
在看了一些树的例子之后,现在来正式地定义树及其构成。
- 节点
-
节点是树的基础部分。它可以有自己的名字,我们称作 “键”。节点也可以带有附加信息,我们称作 “有效载荷”。有效载荷信息对于很多树算法来说不是重点,但它常常在使用树的应用中很重要。
- 边
-
边是树的另一个基础部分。两个节点通过一条边相连,表示它们之间存在关系。除了根节点以外,其他每个节点都仅有一条入边,出边则可能有多条。
- 根节点
-
根节点是树中唯一没有入边的节点。在图 6-2 中,
/就是根节点。 - 路径
-
路径是由边连接的有序节点列表。比如,哺乳纲→食肉目→猫科→猫属→家猫就是一条路径。
- 子节点
-
一个节点通过出边与子节点相连。在图 6-2 中,log/、spool/ 和 yp/ 都是 var/ 的子节点。
- 父节点
-
一个节点是其所有子节点的父节点。在图 6-2 中,var/ 是 log/、spool/ 和 yp/ 的父节点。
- 兄弟节点
-
具有同一父节点的节点互称为兄弟节点。文件系统树中的 etc/ 和 usr/ 就是兄弟节点。
- 子树
-
一个父节点及其所有后代的节点和边构成一棵子树。
- 叶子节点
-
叶子节点没有子节点。比如,图 6-1 中的人和黑猩猩都是叶子节点。
- 层数
-
节点 n 的层数是从根节点到 n 的唯一路径长度。在图 6-1 中,猫属的层数是 5。由定义可知,根节点的层数是 0。
- 高度
-
树的高度是其中节点层数的最大值。图 6-2 中的树高度为 2。
定义基本术语后,就可以进一步给出树的正式定义。实际上,本书将提供两种定义,其中一种涉及节点和边,另一种涉及递归。你在后面会看到,递归定义很有用。
定义一:树由节点及连接节点的边构成。树有以下属性:
-
有一个根节点;
-
除根节点外,其他每个节点都与其唯一的父节点相连;
-
从根节点到其他每个节点都有且仅有一条路径;
-
如果每个节点最多有两个子节点,我们就称这样的树为二叉树。
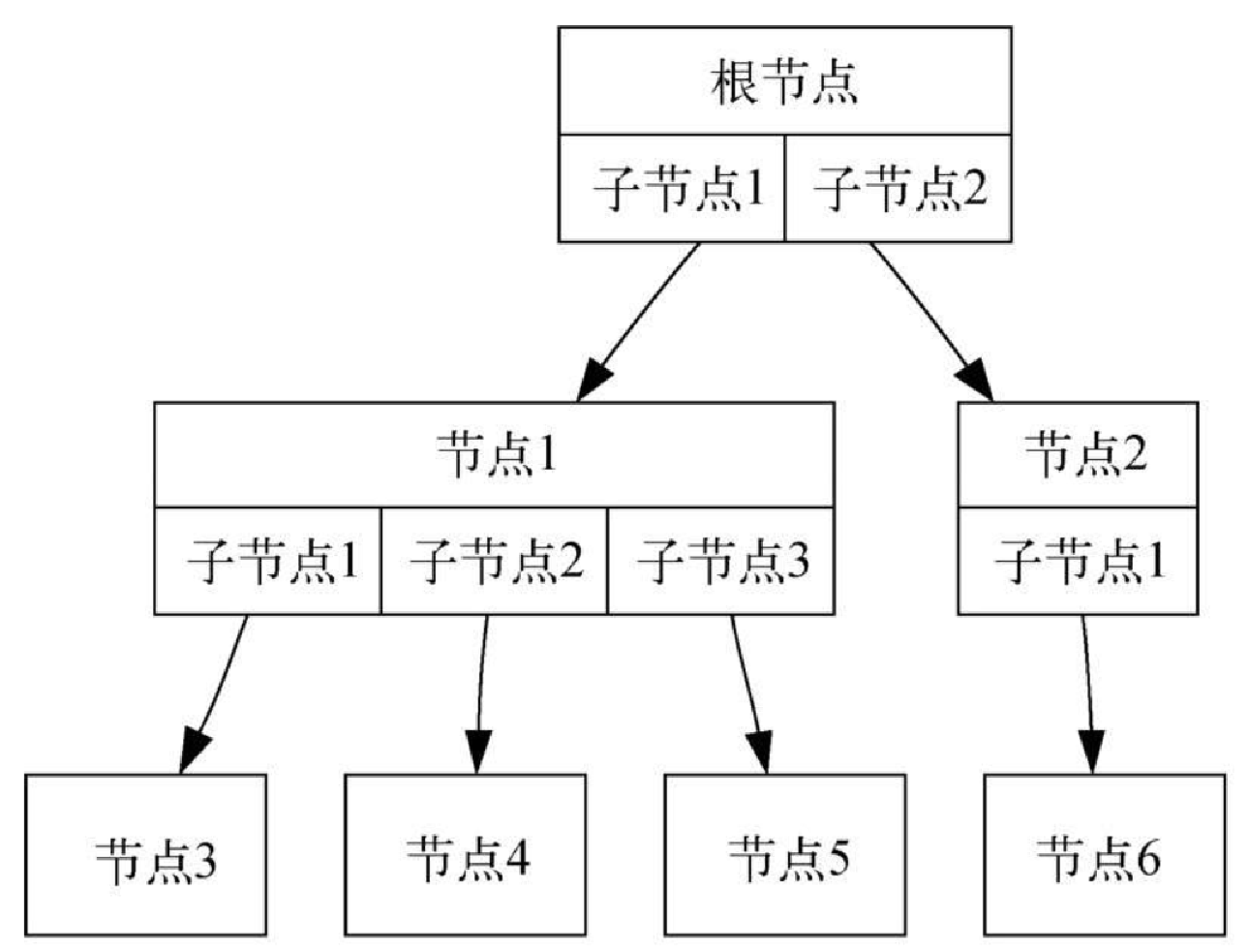
图 6-4 展示了一棵符合定义一的树。边的箭头表示连接方向。
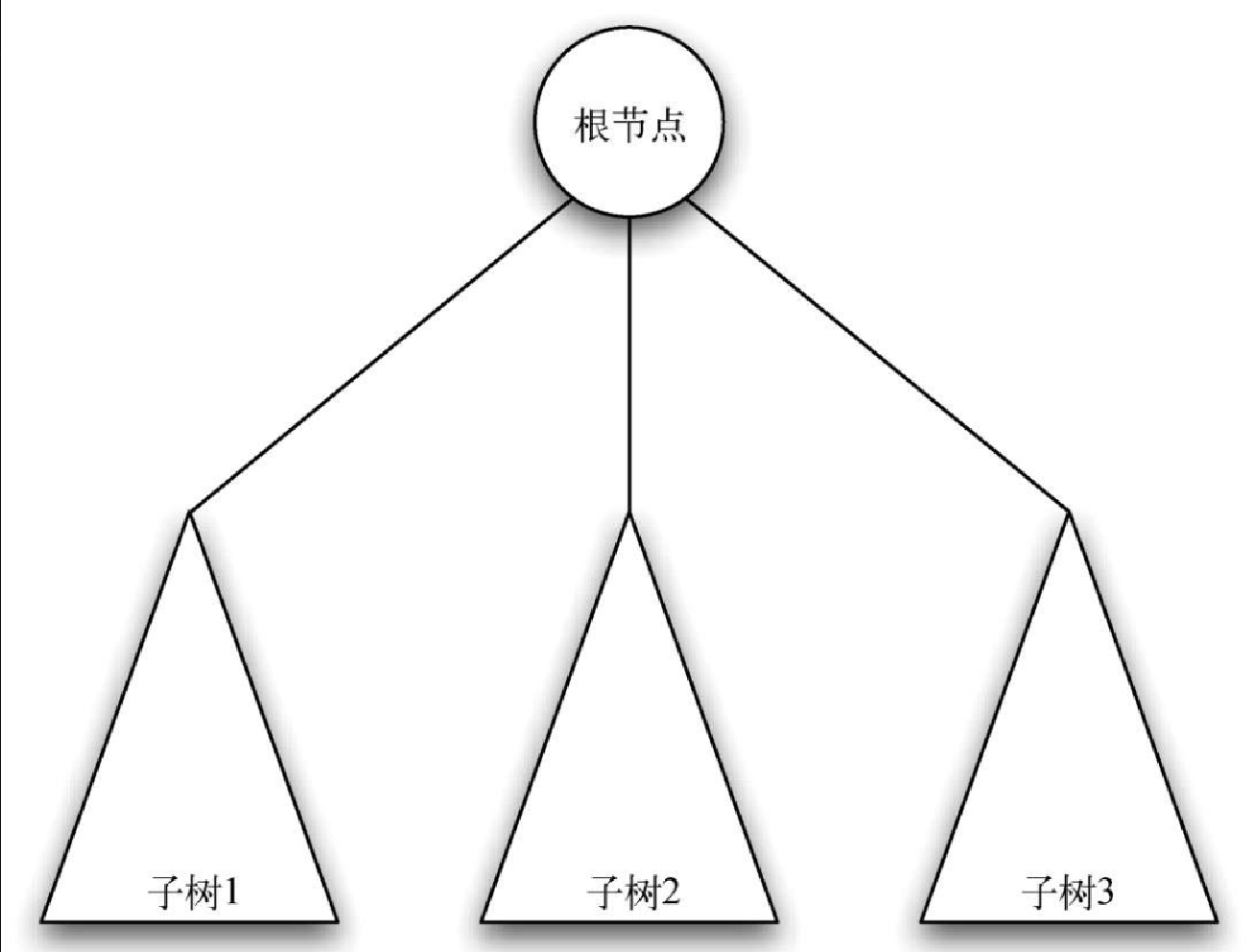
定义二:一棵树要么为空,要么由一个根节点和零棵或多棵子树构成,子树本身也是一棵树。每棵子树的根节点通过一条边连到父树的根节点。图 6-5 展示了树的递归定义。从树的递归定义可知,图中的树至少有 4 个节点,因为三角形代表的子树必定有一个根节点。这棵树或许有更多的节点,但必须更深入地查看子树后才能确定。