探索迷宫

本节探讨一个与蓬勃发展的机器人领域相关的问题：走出迷宫。如果你有一个 Roomba 扫地机器人，或许能利用在本节学到的知识对它进行重新编程。我们要解决的问题是帮助小乌龟走出虚拟的迷宫。迷宫问题源自忒修斯大战牛头怪的古希腊神话传说。相传，在迷宫里杀死牛头怪之后，忒修斯用一个线团找到了迷宫的出口。本节假设小乌龟被放置在迷宫里的某个位置，我们要做的是帮助它爬出迷宫，如图4-12 所示。

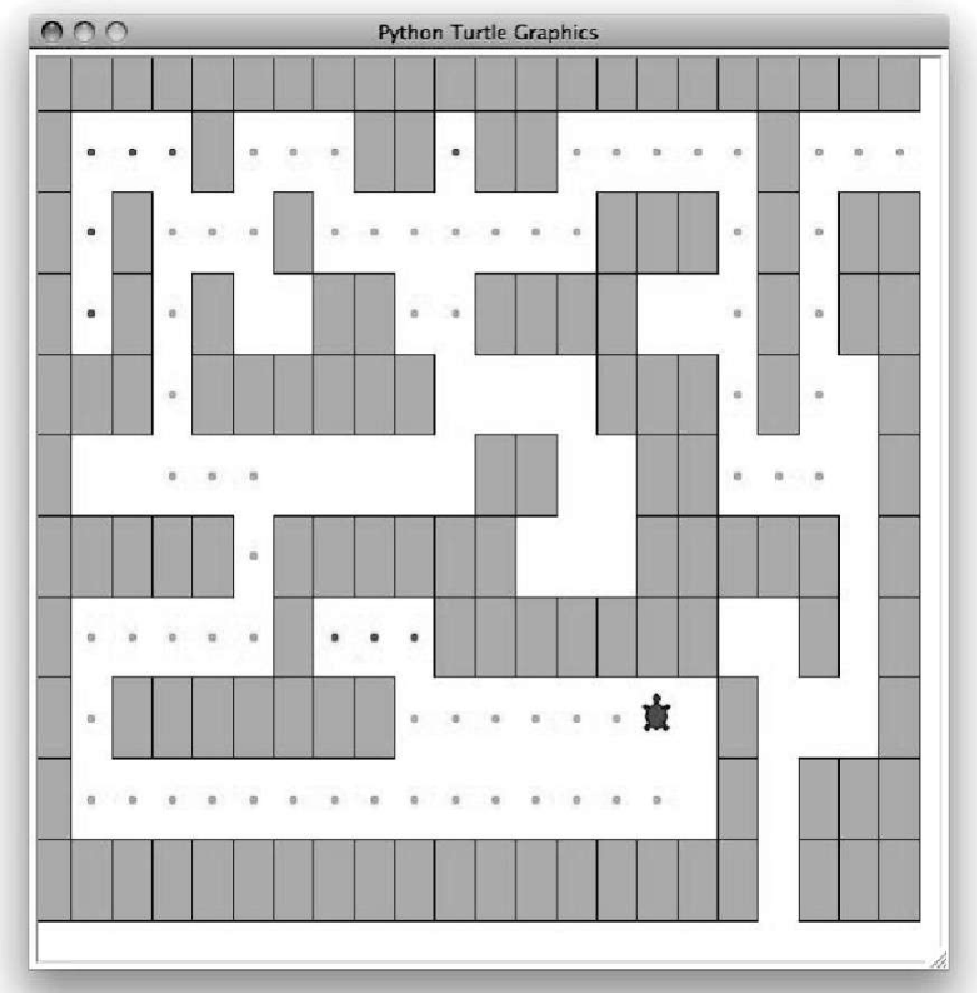
image 2023 12 13 11 31 44 812
Figure 1. 图4-12 帮助小乌龟爬出迷宫

为简单起见，假设迷宫被分成许多格，每一格要么是空的，要么被墙堵上。小乌龟只能沿着空的格子爬行，如果遇到墙，就必须转变方向。它需要如下的系统化过程来找到出路。

  • 从起始位置开始，首先向北移动一格，然后在新的位置再递归地重复本过程。

  • 如果第一步往北行不通，就尝试向南移动一格，然后递归地重复本过程。

  • 如果向南也行不通，就尝试向西移动一格，然后递归地重复本过程。

  • 如果向北、向南和向西都不行，就尝试向东移动一格，然后递归地重复本过程。

  • 如果 4 个方向都不行，就意味着没有出路。

整个过程看上去非常简单，但是有许多细节需要讨论。假设递归过程的第一步是向北移动一格。根据上述过程，下一步也是向北移动一格。但是，如果北面有墙，必须根据递归过程的第二步向南移动一格。不幸的是，向南移动一格之后回到了起点。如果继续执行该递归过程，就会又向北移动一格，然后又退回来，从而陷入无限循环中。所以，必须通过一个策略来记住到过的地方。本例假设小乌龟一边爬，一边丢面包屑。如果往某个方向走一格之后发现有面包屑，就知道应该立刻退回去，然后尝试递归过程的下一步。查看这个算法的代码时会发现，退回去就是从递归函数调用中返回。

和考察其他递归算法时一样，让我们来看看上述算法的基本情况，其中一些可以根据之前的描述猜到。这个算法需要考虑以下 4 种基本情况。

  1. 小乌龟遇到了墙。由于格子被墙堵上，因此无法再继续探索。

  2. 小乌龟遇到了已经走过的格子。在这种情况下，我们不希望它继续探索，不然会陷入循环。

  3. 小乌龟找到了出口。

  4. 四个方向都行不通。

为了使程序运行起来，需要通过一种方式表示迷宫。我们使用 turtle 模块来绘制和探索迷宫，以增加趣味性。迷宫对象提供下列方法，可用于编写搜索算法。

  • __init__ 读入一个代表迷宫的数据文件，初始化迷宫的内部表示，并且找到小乌龟的起始位置。

  • drawMaze 在屏幕上的一个窗口中绘制迷宫。

  • updatePosition 更新迷宫的内部表示，并且修改小乌龟在迷宫中的位置。

  • isExit 检查小乌龟的当前位置是否为迷宫的出口。

除此之外，Maze 类还重载了索引运算符[]，以便算法访问任一格的状态。

代码清单4-10 展示了搜索函数 searchFrom 的代码。该函数接受 3 个参数：迷宫对象、起始行，以及起始列。由于该函数的每一次递归调用在逻辑上都是重新开始搜索的，因此定义成接受 3 个参数非常重要。

代码清单4-10 迷宫搜索函数searchFrom
def searchFrom(maze, startRow, startColumn):
    maze.updatePosition(startRow, startColumn)
   #  Check for base cases:
   #  1. We have run into an obstacle, return false
   if maze[startRow][startColumn] == OBSTACLE :
        return False
    #  2. We have found a square that has already been explored
    if maze[startRow][startColumn] == TRIED:
        return False
    # 3. Success, an outside edge not occupied by an obstacle
    if maze.isExit(startRow,startColumn):
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
        return True
    maze.updatePosition(startRow, startColumn, TRIED)

    # Otherwise, use logical short circuiting to try each
    # direction in turn (if needed)
    found = searchFrom(maze, startRow-1, startColumn) or \
            searchFrom(maze, startRow+1, startColumn) or \
            searchFrom(maze, startRow, startColumn-1) or \
            searchFrom(maze, startRow, startColumn+1)
    if found:
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
    else:
        maze.updatePosition(startRow, startColumn, DEAD_END)
    return found

该函数做的第一件事就是调用 updatePosition（第 2 行）。这样做是为了对算法进行可视化，以便我们看到小乌龟如何在迷宫中寻找出口。接着，该函数检查前3种基本情况：是否遇到了墙（第 5 行）？是否遇到了已经走过的格子（第 8 行）？是否找到了出口（第 11 行）？如果没有一种情况符合，则继续递归搜索。

递归搜索调用了 4 个 searchFrom。很难预测一共会进行多少个递归调用，这是因为它们都是用布尔运算符 or 连接起来的。如果第一次调用 searchFrom 后返回 True，那么就不必进行后续的调用。可以这样理解：向北移动一格是离开迷宫的路径上的一步。如果向北没有能够走出迷宫，那么就会尝试下一个递归调用，即向南移动。如果向南失败了，就尝试向西，最后向东。如果所有的递归调用都失败了，就说明遇到了死胡同。请下载或自己输入代码，改变 4 个递归调用的顺序，看看结果如何。

Maze 类的方法定义如代码清单4-11～代码清单4-13所示。__init__ 方法只接受一个参数，即文件名。该文本文件包含迷宫的信息，其中 + 代表墙，空格代表空的格子，S 代表起始位置。图4-13 是迷宫数据文件的例子。迷宫的内部表示是一个列表，其元素也是列表。实例变量 mazelist 的每一行是一个列表，其中每一格包含一个字符。对于图4-13 对应的数据文件，其内部表示如下。

image 2023 12 13 11 40 19 943
Figure 2. 图4-13 迷宫数据文件示例

drawMaze 方法使用以上内部表示在屏幕上绘制初始的迷宫，如图4-12 所示。

updatePosition 方法使用相同的内部表示检查小乌龟是否遇到了墙。同时，它会更改内部表示，使用 . 和 - 来分别表示小乌龟遇到了走过的格子和死胡同。此外，updatePosition 方法还使用辅助函数 moveTurtle 和 dropBreadcrumb 来更新屏幕上的信息。

isExit 方法检查小乌龟的当前位置是否为出口，条件是小乌龟已经爬到迷宫边缘：第 0 行、第 0 列、最后一行或者最后一列。

代码清单4-11 Maze类
class Maze:
    def __init__(self,mazeFileName):
        rowsInMaze = 0
        columnsInMaze = 0
        self.mazelist = []
        mazeFile = open(mazeFileName,'r')
        rowsInMaze = 0
        for line in mazeFile:
            rowList = []
            col = 0
            for ch in line[:-1]:
                rowList.append(ch)
                if ch == 'S':
                    self.startRow = rowsInMaze
                    self.startCol = col
                col = col + 1
            rowsInMaze = rowsInMaze + 1
            self.mazelist.append(rowList)
            columnsInMaze = len(rowList)

        self.rowsInMaze = rowsInMaze
        self.columnsInMaze = columnsInMaze
        self.xTranslate = -columnsInMaze/2
        self.yTranslate = rowsInMaze/2
        self.t = Turtle(shape='turtle')
        setup(width=600,height=600)
        setworldcoordinates(-(columnsInMaze-1)/2-.5,
                            -(rowsInMaze-1)/2-.5,
                            (columnsInMaze-1)/2+.5,
                            (rowsInMaze-1)/2+.5)
代码清单4-12 Maze类
def drawMaze(self):
    for y in range(self.rowsInMaze):
        for x in range(self.columnsInMaze):
            if self.mazelist[y][x] == OBSTACLE:
                self.drawCenteredBox(x+self.xTranslate,
                                     -y+self.yTranslate,
                                     'tan')
    self.t.color('black','blue')

def drawCenteredBox(self,x,y,color):
    tracer(0)
    self.t.up()
    self.t.goto(x-.5,y-.5)
    self.t.color('black',color)
    self.t.setheading(90)
    self.t.down()
    self.t.begin_fill()
    for i in range(4):
        self.t.forward(1)
        self.t.right(90)
    self.t.end_fill()
    update()
    tracer(1)

def moveTurtle(self,x,y):
    self.t.up()
    self.t.setheading(self.t.towards(x+self.xTranslate,
                                     -y+self.yTranslate))
    self.t.goto(x+self.xTranslate,-y+self.yTranslate)

def dropBreadcrumb(self,color):
    self.t.dot(color)

def updatePosition(self,row,col,val=None):
    if val:
        self.mazelist[row][col] = val
    self.moveTurtle(col,row)

    if val == PART_OF_PATH:
        color = 'green'
    elif val == OBSTACLE:
        color = 'red'
    elif val == TRIED:
        color = 'black'
    elif val == DEAD_END:
        color = 'red'
    else:
        color = None

    if color:
        self.dropBreadcrumb(color)
代码清单4-13 Maze类
def isExit(self,row,col):
     return (row == 0 or
             row == self.rowsInMaze-1 or
             col == 0 or
             col == self.columnsInMaze-1 )

def __getitem__(self,idx):
     return self.mazelist[idx]