小结

本章介绍了图的抽象数据类型，以及一些实现方式。如果能将一个问题用图表示出来，那么就可以利用图算法加以解决。对于解决下列问题，图非常有用。

  • 利用宽度优先搜索找到无权重的最短路径。

  • 利用 Dijkstra 算法求解带权重的最短路径。

  • 利用深度优先搜索来探索图。

  • 利用强连通单元来简化图。

  • 利用拓扑排序为任务排序。

  • 利用最小生成树广播消息。

讨论题

  1. 画出以下邻接矩阵对应的图。

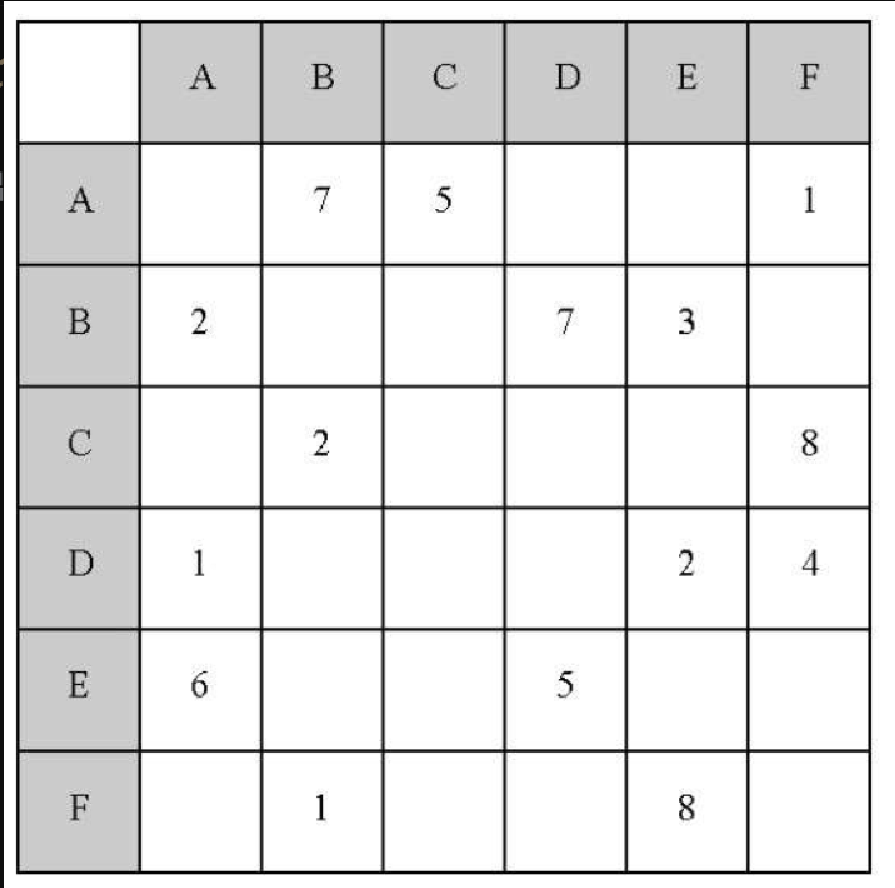
    image 2023 12 14 09 56 04 885

  2. 画出符合以下条件的图。

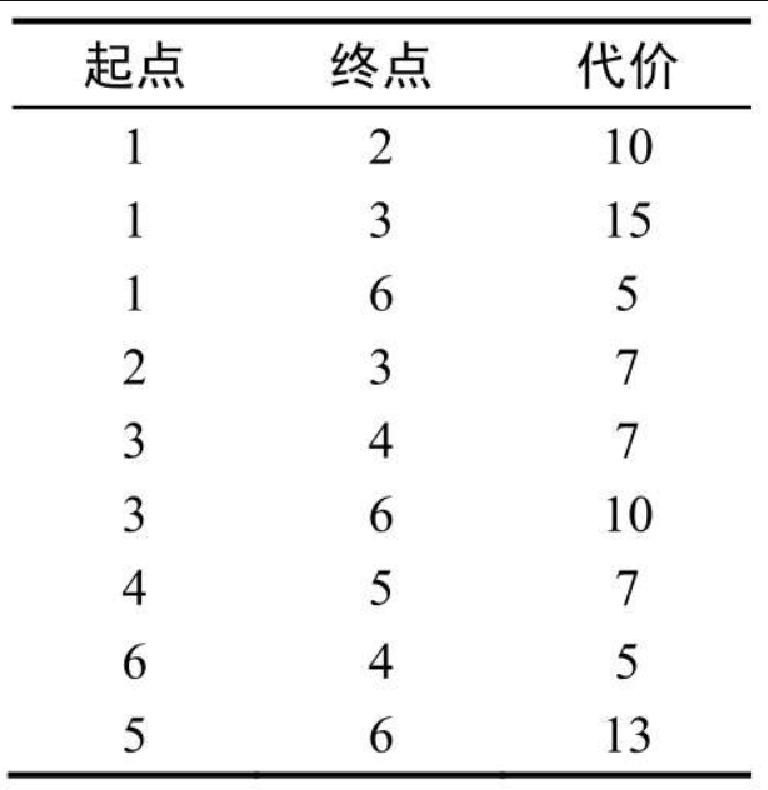
    image 2023 12 14 09 56 33 316

  3. 忽略权重，针对讨论题1中的图进行宽度优先搜索。

  4. 在代码清单7-3 中，buildGraph 函数的时间复杂度是多少？

  5. 推导出拓扑排序算法的时间复杂度。

  6. 推导出强连通单元算法的时间复杂度。

  7. 将 Dijkstra 算法应用于讨论题 2 中的图，展示每一步。

  8. 利用 Prim 算法为讨论题 1 中的图找到最小生成树。

  9. 画出发送电子邮件所需步骤的依赖图，并应用拓扑排序算法。

  10. 推导出骑士周游问题算法的时间复杂度中底数的表达式。

  11. 解释通用深度优先搜索不适用于骑士周游问题的原因。

  12. 推导出 Prim 算法的时间复杂度。

编程练习

  1. 修改深度优先搜索函数，以进行拓扑排序。

  2. 修改深度优先搜索函数，以计算强连通单元。

  3. 为 Graph 类编写 transpose 方法。

  4. 使用宽度优先搜索实现一个算法，用以计算从每一个顶点到其余所有顶点的最短路径。这被称为所有对最短路径。

  5. 使用宽度优先搜索修改第 4 章中的迷宫程序，从而找到走出迷宫的最短路径。

  6. 写一个程序来解决这样一个问题：有 2 个坛子，其中一个的容量是 4 加仑，另一个的是 3 加仑。坛子上都没有刻度线。可以用水泵将它们装满水。如何使 4 加仑的坛子最后装有 2 加仑的水？

  7. 扩展练习 6 中的程序，将坛子的容量和较大的坛子中最后的水量作为参数。

  8. 写一个程序来解决这样一个问题：3 只羚羊和 3 只狮子准备乘船过河，河边有一艘能容纳 2 只动物的小船。但是，如果两侧河岸上的狮子数量大于羚羊数量，羚羊就会被吃掉。找到运送办法，使得所有动物都能安全渡河。