强连通单元
接下来将注意力转向规模庞大的图。我们将以互联网主机与各个网页构成的图为例,学习其他几种算法。首先讨论网页。
在互联网上,各种网页形成一张大型的有向图,谷歌和必应等搜索引擎正是利用了这一事实。要将互联网转换成一张图,我们将网页当作顶点,将超链接当作连接顶点的边。图7-21 展示了以路德学院计算机系的主页作为起点的网页连接图的一小部分。由于这张图的规模庞大,因此我们限制网页与起点页之间的链接数不超过 10 个。
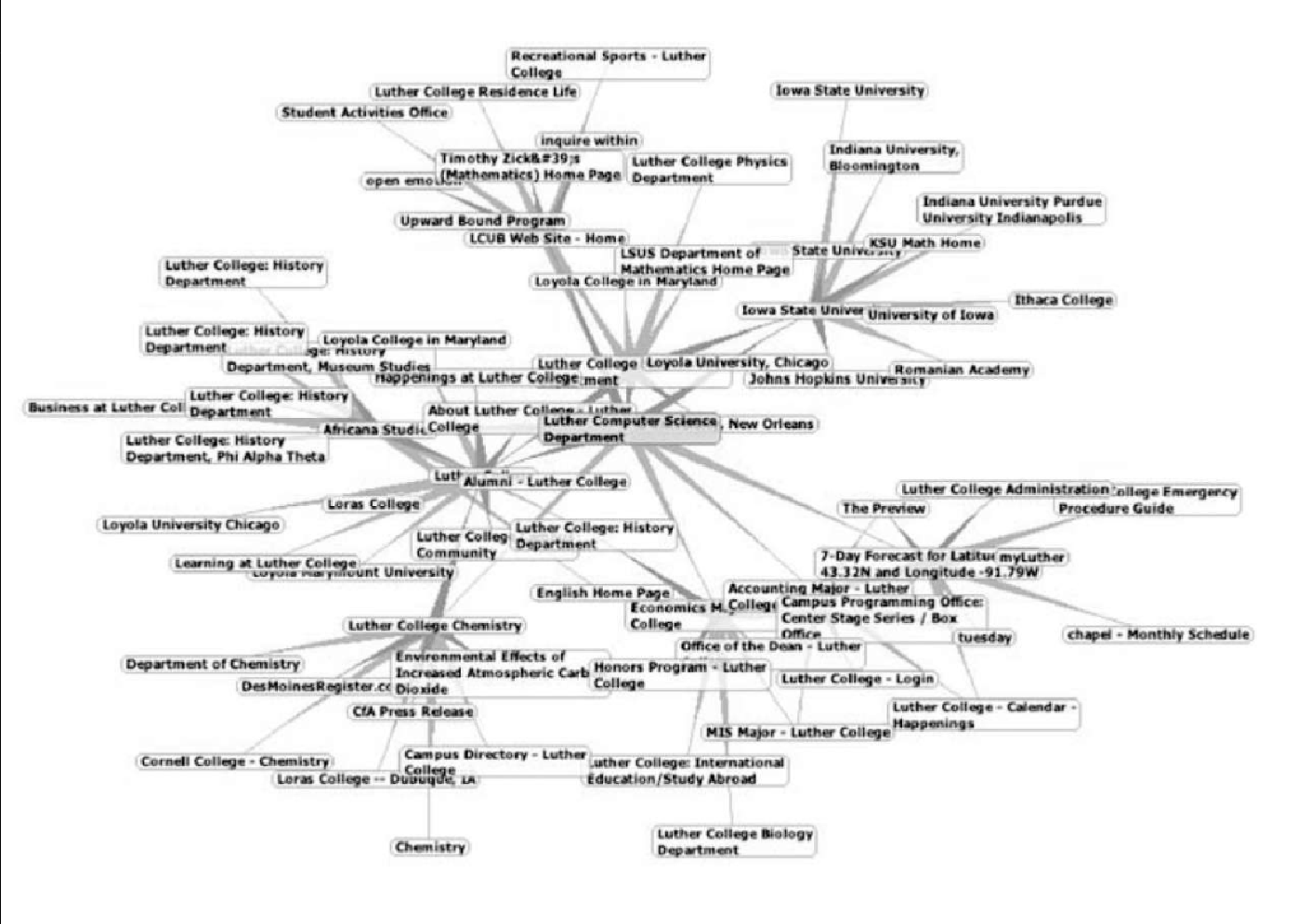
仔细研究图7-21,会有一些非常有趣的发现。首先,图中的很多网页来自路德学院的其他网站。其次,一些链接指向爱荷华州的其他学校。最后,一些链接指向其他文理学院。由此可以得出这样的结论:网络具有一种基础结构,使得在某种程度上相似的网页相互聚集。
通过一种叫作强连通单元的图算法,可以找出图中高度连通的顶点簇。对于图 G,强连通单元 C 为最大的顶点子集 C⊂V,其中对于每一对顶点 v, w∈C,都有一条从 v 到 w 的路径和一条从 w 到 v 的路径。
图7-22 展示了一个包含 3 个强连通单元的简单图。不同的强连通单元通过不同的阴影来表现。
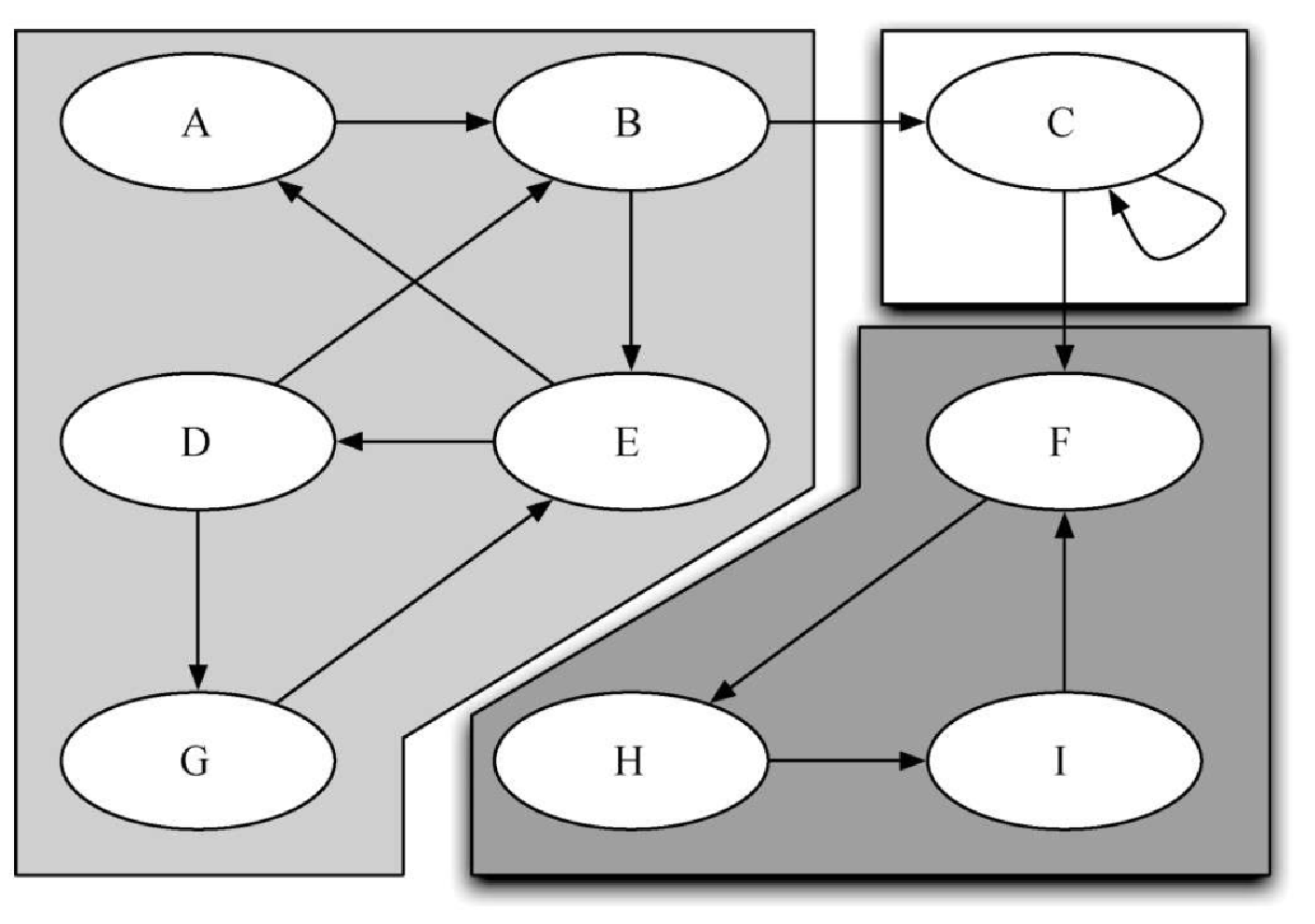
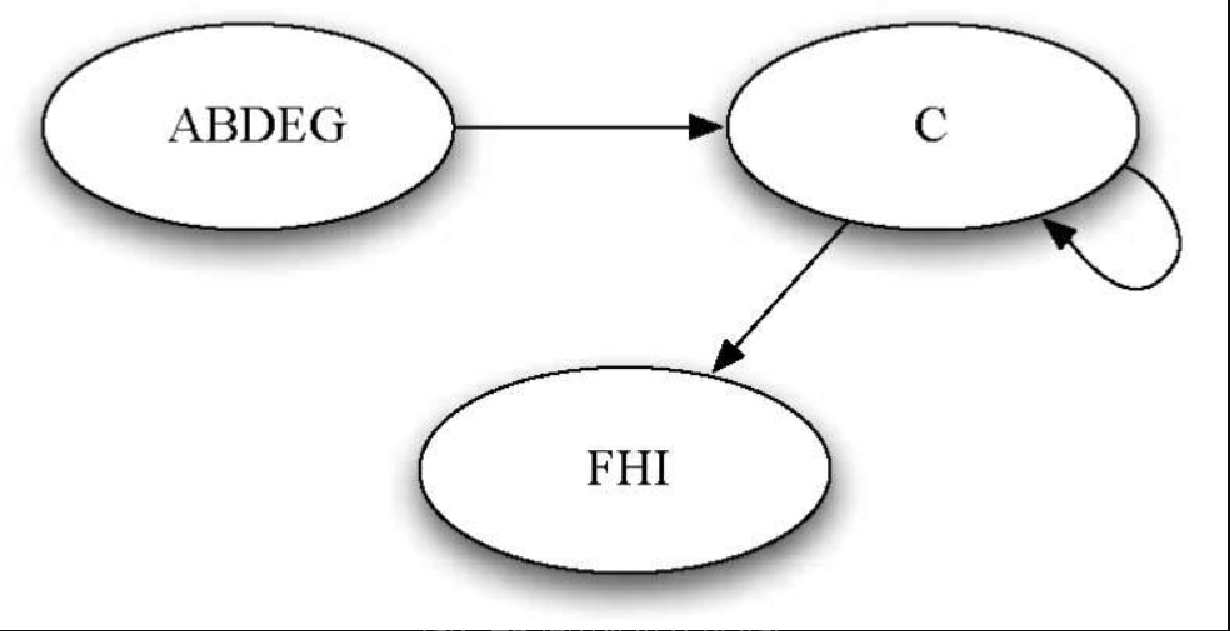
定义强连通单元之后,就可以把强连通单元中的所有顶点组合成单个顶点,从而将图简化。图7-23 是图7-22 的简化版。
利用深度优先搜索,我们可以再次创建强大高效的算法。在学习强连通单元算法之前,还要再看一个定义。图 G 的转置图被定义为 GT,其中所有的边都与图 G 的边反向。这意味着,如果在图 G 中有一条由 A 到 B 的边,那么在 GT 中就会有一条由 B 到 A 的边。图7-24 展示了一个简单图及其转置图。
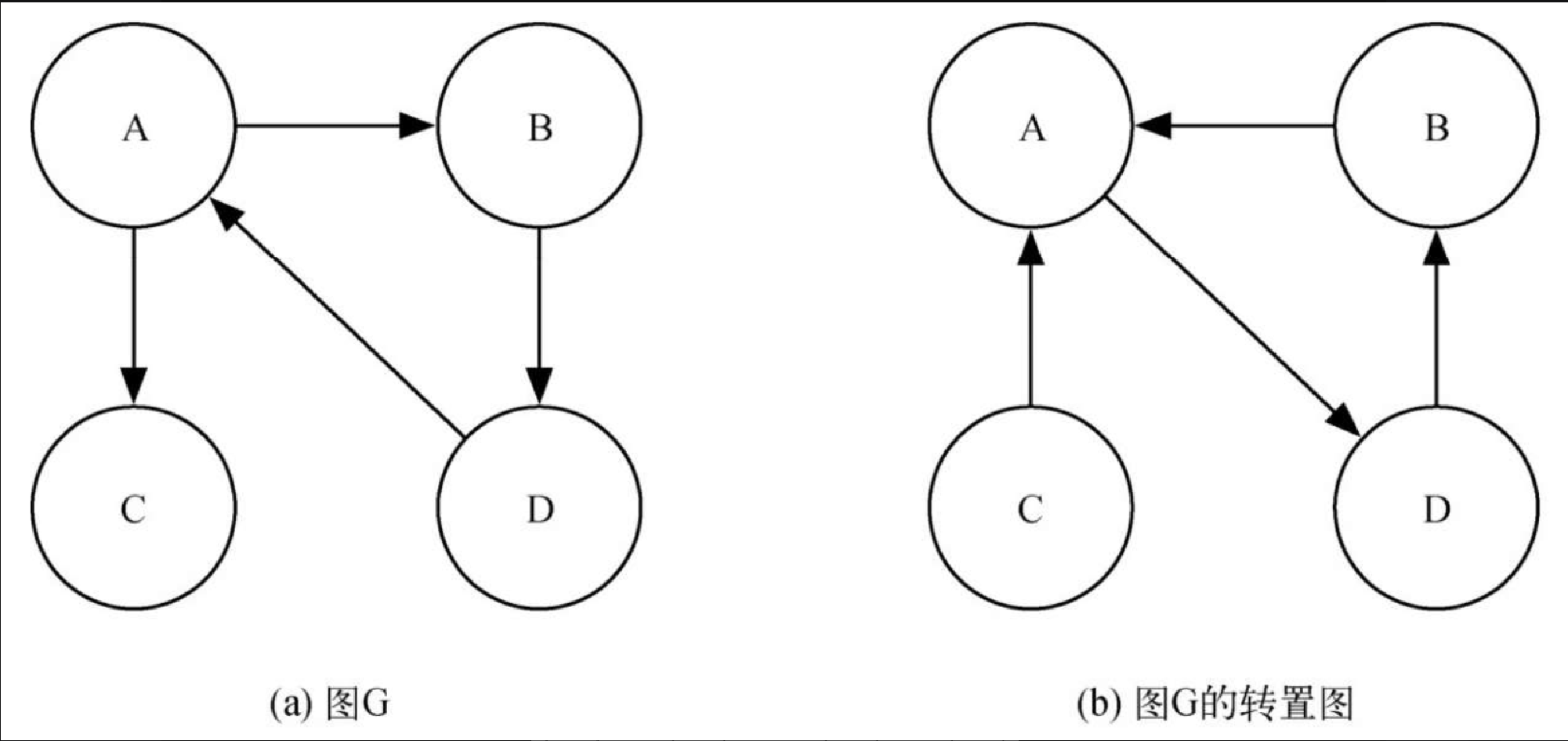
再次观察图 7-24。注意,图7-24a 中有 2 个强连通单元,图7-24b 中也是如此。
以下是计算强连通单元的算法。
-
对图 G 调用 dfs,以计算每一个顶点的结束时间。
-
计算图 GT。
-
对图 GT 调用 dfs,但是在主循环中,按照结束时间的递减顺序访问顶点。
-
第 3 步得到的深度优先森林中的每一棵树都是一个强连通单元。输出每一棵树中的顶点的 id。
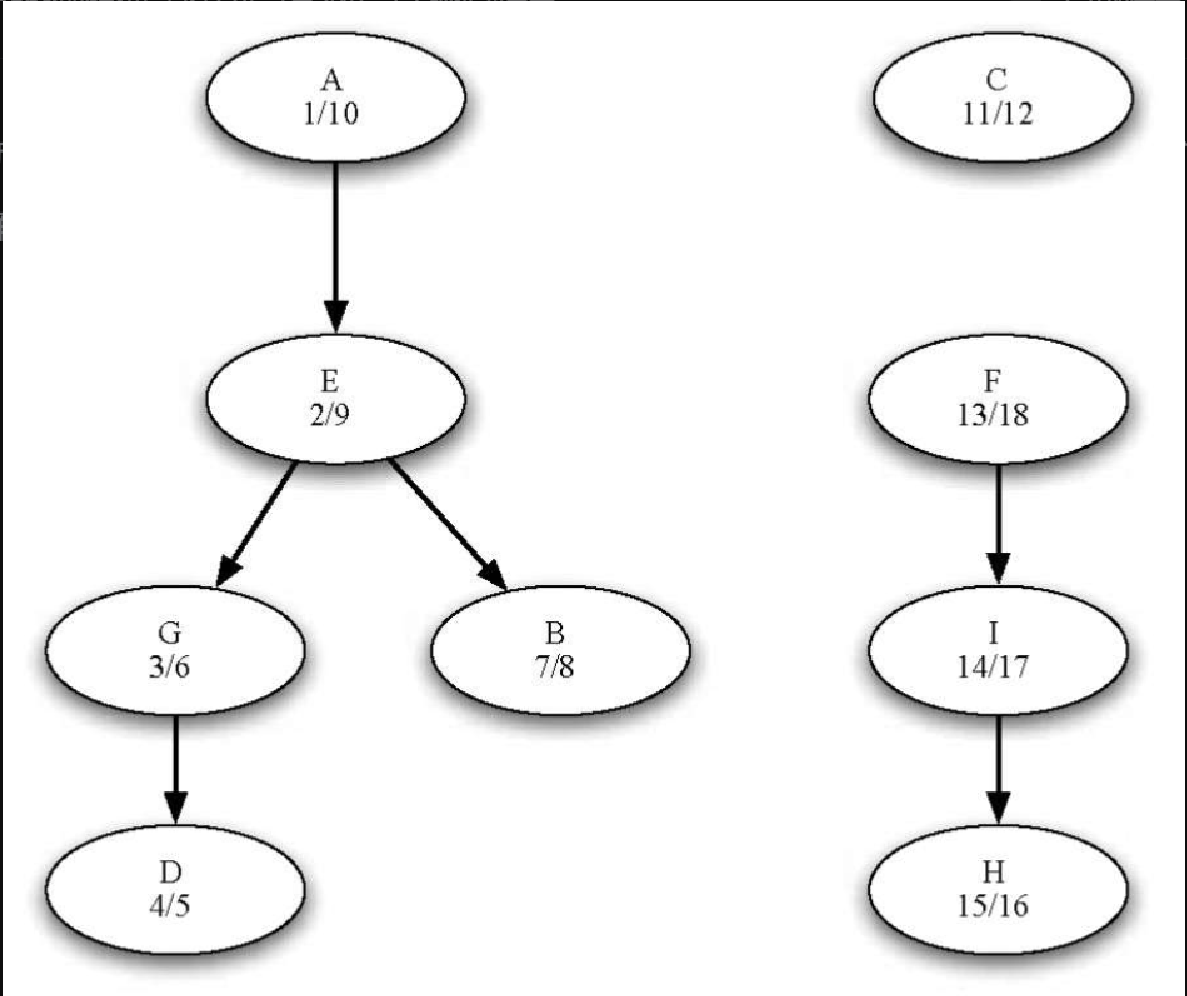
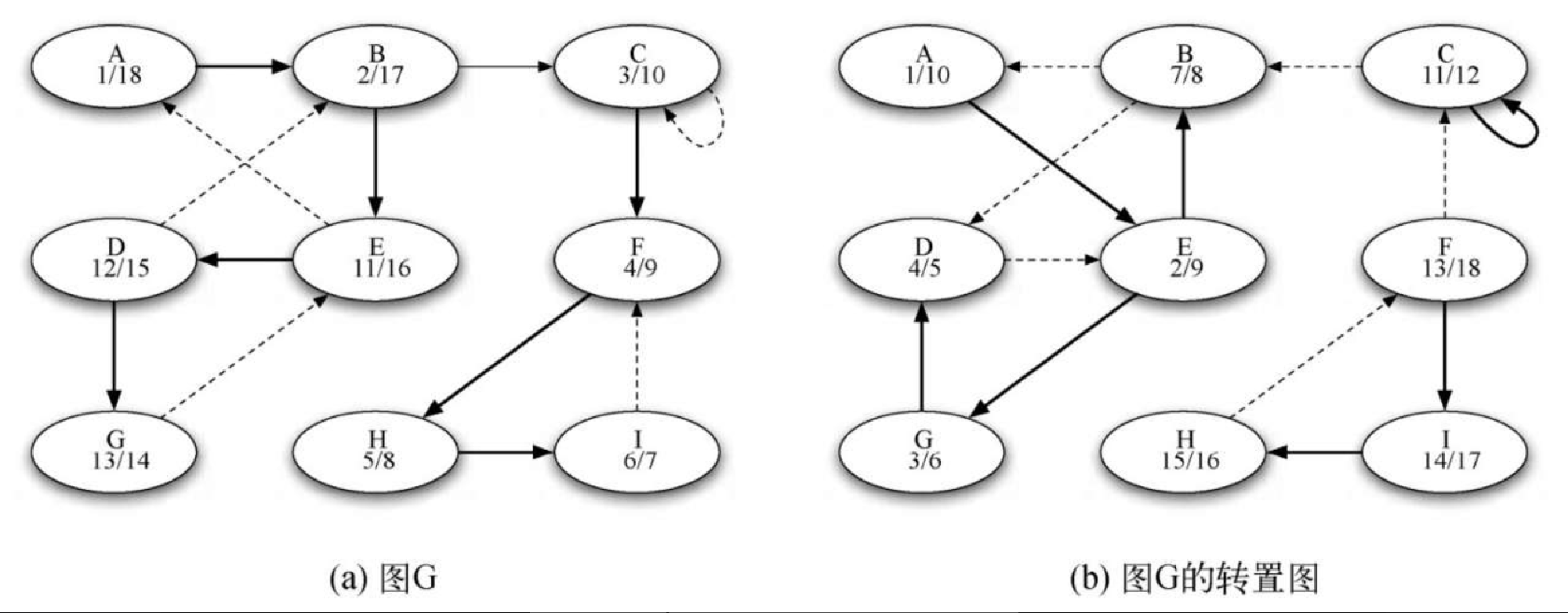
以图7-22 为例,让我们来逐步分析。图7-25a 展示了用深度优先搜索算法对原图计算得到的发现时间和结束时间,图7-25b 展示了用深度优先搜索算法在转置图上得到的发现时间和结束时间。
最后,图7-26 展示了由强连通单元算法在第 3 步生成的森林,其中有 3 棵树。我们没有提供强连通单元算法的 Python 代码,而是将其作为编程练习。