利用二叉堆实现优先级队列

第 3 章介绍过队列这一先进先出的数据结构。队列有一个重要的变体，叫作优先级队列。和队列一样，优先级队列从头部移除元素，不过元素的逻辑顺序是由优先级决定的。优先级最高的元素在最前，优先级最低的元素在最后。因此，当一个元素入队时，它可能直接被移到优先级队列的头部。你在第 7 章会看到，对于一些图算法来说，优先级队列是一个有用的数据结构。

你或许可以想到一些使用排序函数和列表实现优先级队列的简单方法。但是，就时间复杂度而言，列表的插入操作是 \$O(n)\$，排序操作是 \$O(nlog n)\$。其实，效率可以更高。实现优先级队列的经典方法是使用叫作二叉堆的数据结构。二叉堆的入队操作和出队操作均可达到 \$O(log n)\$。

二叉堆学起来很有意思，它画出来很像一棵树，但实现时只用一个列表作为内部表示。二叉堆有两个常见的变体：最小堆（最小的元素一直在队首）与最大堆（最大的元素一直在队首）。本节将实现最小堆，并将最大堆的实现留作练习。

二叉堆的操作

我们将实现以下基本的二叉堆方法。

  • BinaryHeap() 新建一个空的二叉堆。

  • insert(k) 往堆中加入一个新元素。

  • findMin() 返回最小的元素，元素留在堆中。

  • delMin() 返回最小的元素，并将该元素从堆中移除。

  • isEmpty() 在堆为空时返回 True，否则返回 False。

  • size() 返回堆中元素的个数。

  • buildHeap(list) 根据一个列表创建堆。

以下 Python 会话展示了一些二叉堆方法的用法。

>>> from pythonds.trees import BinaryHeap
>>> bh = BinaryHeap()
>>> bh.insert(5)
>>> bh.insert(7)
>>> bh.insert(3)
>>> bh.insert(11)
>>> print(bh.delMin())
3
>>> print(bh.delMin())
5
>>> print(bh.delMin())
7
>>> print(bh.delMin())
11

二叉堆的实现

  1. 结构属性

    为了使二叉堆能高效地工作，我们利用树的对数性质来表示它。你会在 6.7.3 节学到，为了保证对数性能，必须维持树的平衡。平衡的二叉树是指，其根节点的左右子树含有数量大致相等的节点。在实现二叉堆时，我们通过创建一棵完全二叉树来维持树的平衡。在完全二叉树中，除了最底层，其他每一层的节点都是满的。在最底层，我们从左往右填充节点。图 6-14 展示了完全二叉树的一个例子。

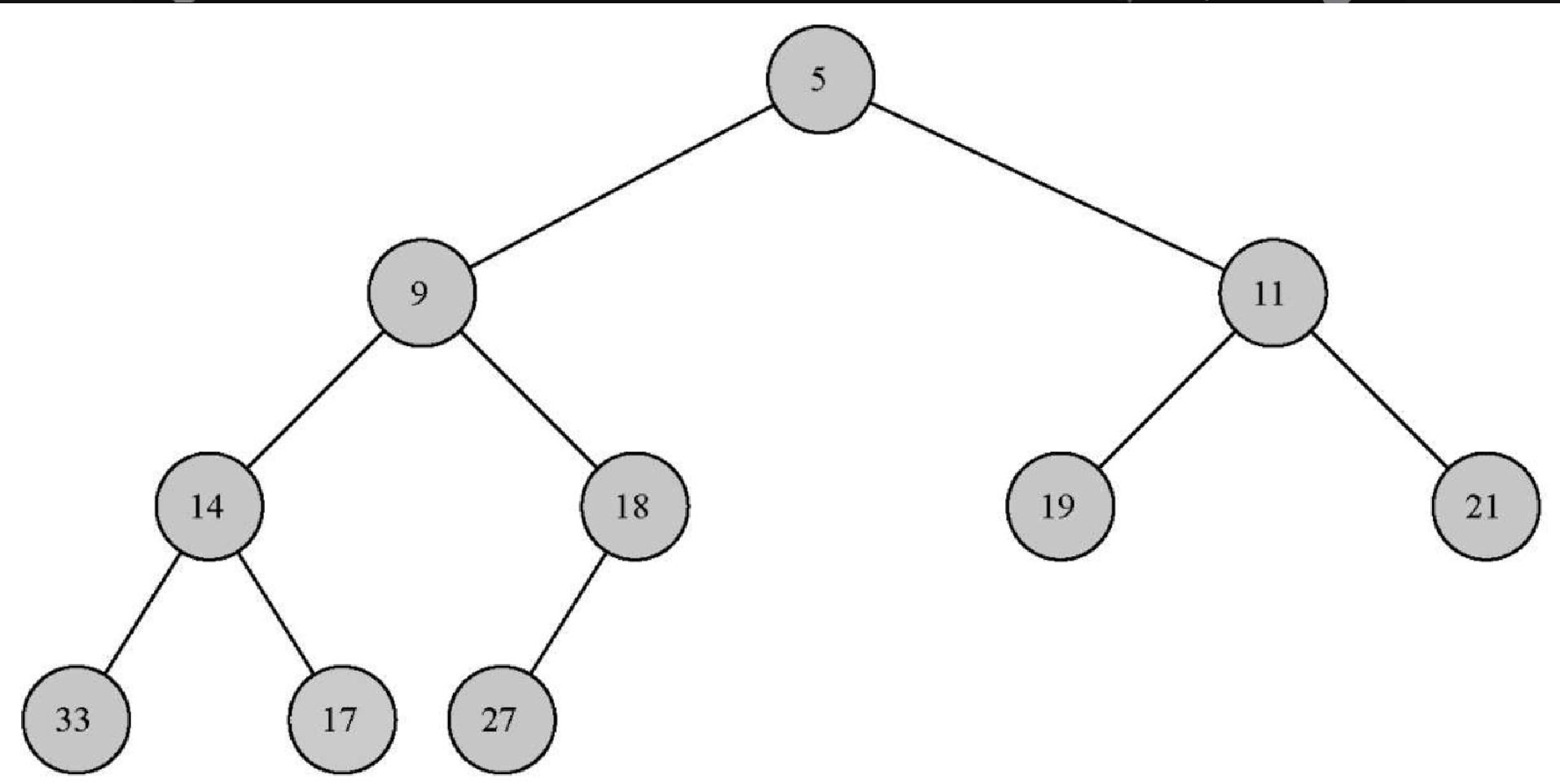    image 2023 12 13 18 44 09 504
    Figure 1. 图6-14 完全二叉树

    完全二叉树的另一个有趣之处在于，可以用一个列表来表示它，而不需要采用 “列表之列表” 或 “节点与引用” 表示法。由于树是完全的，因此对于在列表中处于位置p的节点来说，它的左子节点正好处于位置 2p；同理，右子节点处于位置 2p+1。若要找到树中任意节点的父节点，只需使用 Python 的整数除法即可。给定列表中位置 n 处的节点，其父节点的位置就是 n/2。图 6-15 展示了一棵完全二叉树，并给出了列表表示。树的列表表示——加上这个 “完全” 的结构性质——让我们得以通过一些简单的数学运算遍历完全二叉树。我们会看到，这也有助于高效地实现二叉堆。

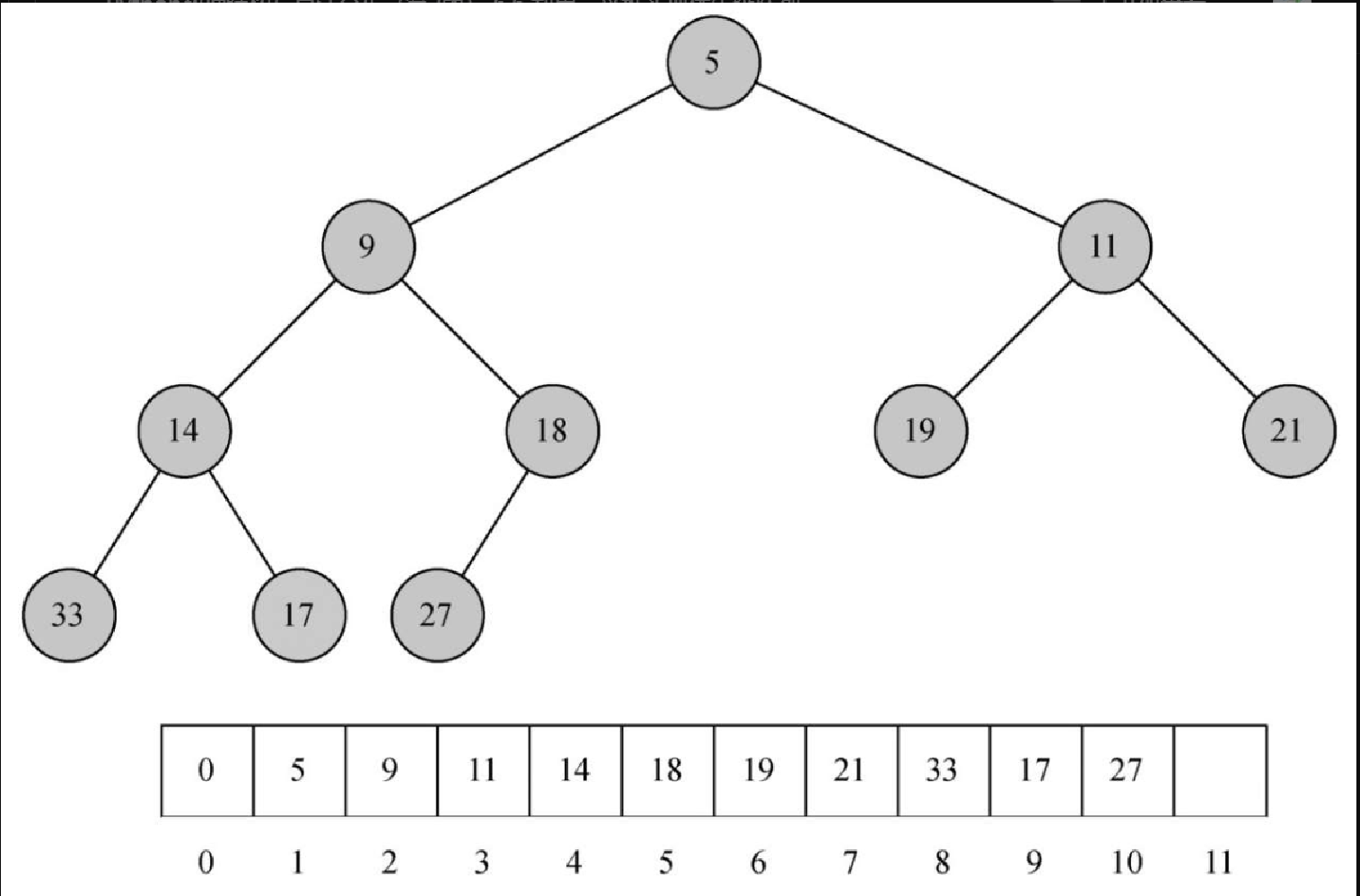    image 2023 12 13 18 45 08 358
    Figure 2. 图6-15 一棵完全二叉树及其列表表示

  2. 堆的有序性

    我们用来存储堆元素的方法依赖于堆的有序性。堆的有序性是指：对于堆中任意元素x 及其父元素 p, p 都不大于 x。图 6-15 也展示出完全二叉树具备堆的有序性。

  3. 堆操作

首先实现二叉堆的构造方法。既然用一个列表就可以表示整个二叉堆，那么构造方法要做的就是初始化这个列表与属性 currentSize，用于记录堆的当前大小。代码清单 6-17 给出了构造方法的 Python 代码。列表 heapList 的第一个元素是 0，它的唯一用途是为了使后续的方法可以使用整数除法。

代码清单6-17 新建二叉堆
class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0

接下来实现 insert 方法。将元素加入列表的最简单、最高效的方法就是将元素追加到列表的末尾。追加操作的优点在于，它能保证完全树的性质，但缺点是很可能会破坏堆的结构性质。不过可以写一个方法，通过比较新元素与其父元素来重新获得堆的结构性质。如果新元素小于其父元素，就将二者交换。图 6-16 展示了将新元素放到正确位置上所需的一系列交换操作。

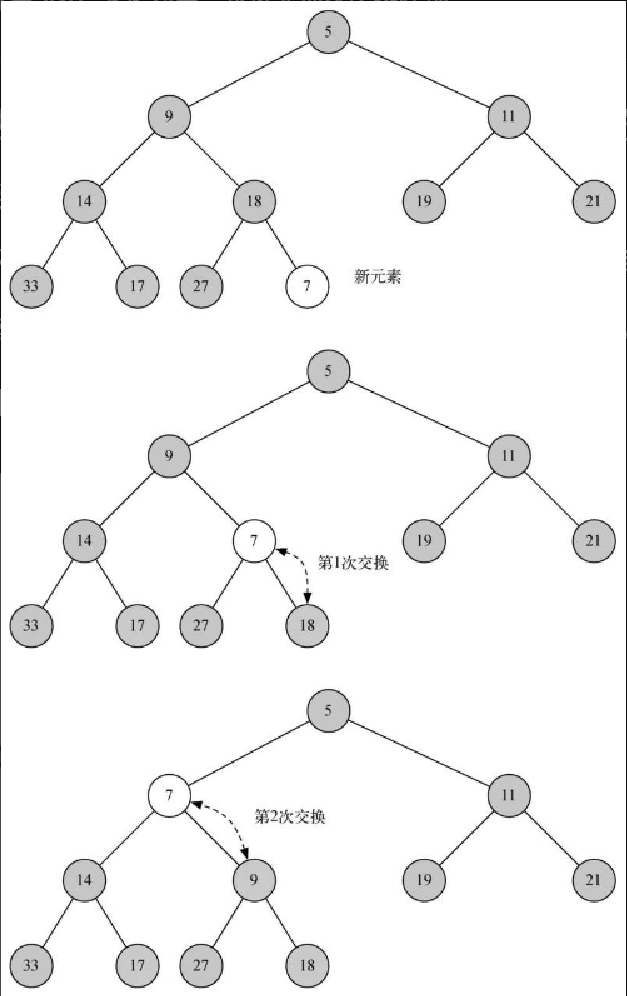
image 2023 12 13 18 47 57 127
Figure 3. 图6-16 将新元素往上移到正确位置

注意，将元素往上移时，其实是在新元素及其父元素之间重建堆的结构性质。此外，也保留了兄弟元素之间的堆性质。当然，如果新元素很小，需要继续往上一层交换。代码清单 6-18 给出了 percUp 方法的代码，该方法将元素一直沿着树向上移动，直到重获堆的结构性质。此时，heapList 中的元素 0 正好能发挥重要作用。我们使用整数除法计算任意节点的父节点。就当前节点而言，父节点的下标就是当前节点的下标除以 2。

代码清单6-18 percUp方法
def percUp(self,i):
    while i // 2 > 0:
      if self.heapList[i] < self.heapList[i // 2]:
         tmp = self.heapList[i // 2]
         self.heapList[i // 2] = self.heapList[i]
         self.heapList[i] = tmp
      i = i // 2

现在准备好编写 insert 方法了。代码清单 6-19 给出了该方法的 Python 代码。其实，insert 方法的大部分工作是由 percUp 方法完成的。当元素被追加到树中之后，percUp 方法将其移到正确的位置。

代码清单6-19 向二叉堆中新加元素
def insert(self,k):
    self.heapList.append(k)
    self.currentSize = self.currentSize + 1
    self.percUp(self.currentSize)

正确定义 insert 方法后，就可以编写 delMin 方法。既然堆的结构性质要求根节点是树的最小元素，那么查找最小值就很简单。delMin 方法的难点在于，如何在移除根节点之后重获堆的结构性质和有序性。可以分两步重建堆。第一步，取出列表中的最后一个元素，将其移到根节点的位置。移动最后一个元素保证了堆的结构性质，但可能会破坏二叉堆的有序性。第二步，将新的根节点沿着树推到正确的位置，以重获堆的有序性。图 6-17 展示了将新的根节点移动到正确位置所需的一系列交换操作。

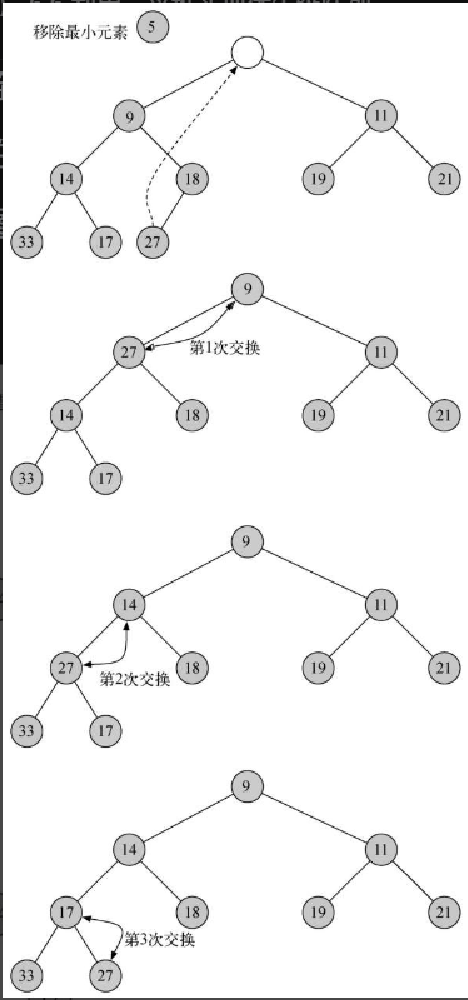
image 2023 12 13 18 51 03 683
Figure 4. 图6-17 将根节点往下移到正确位置

为了维持堆的有序性，只需交换根节点与它的最小子节点即可。重复节点与子节点的交换过程，直到节点比其两个子节点都小。代码清单 6-20 给出了 percDown 方法和 minChild 方法的 Python 代码。

代码清单6-20 percDown方法和minChild方法
def percDown(self,i):
    while (i * 2) <= self.currentSize:
        mc = self.minChild(i)
        if self.heapList[i] > self.heapList[mc]:
            tmp = self.heapList[i]
            self.heapList[i] = self.heapList[mc]
            self.heapList[mc] = tmp
        i = mc

def minChild(self,i):
    if i * 2 + 1 > self.currentSize:
        return i * 2
    else:
        if self.heapList[i*2] < self.heapList[i*2+1]:
            return i * 2
        else:
            return i * 2 + 1

delMin 方法如代码清单 6-21 所示。同样，主要工作也由辅助函数完成。本例中的辅助函数是 percDown。

代码清单6-21 从二叉堆中删除最小的元素
def delMin(self):
    retval = self.heapList[1]
    self.heapList[1] = self.heapList[self.currentSize]
    self.currentSize = self.currentSize - 1
    self.heapList.pop()
    self.percDown(1)
    return retval

关于二叉堆，还有最后一点需要讨论。我们来看看根据元素列表构建整个堆的方法。你首先想到的方法或许是这样的：给定元素列表，每次插入一个元素，构建一个堆。由于是从列表只有一个元素的情况开始，并且列表是有序的，因此可以采用二分搜索算法找到下一个元素的正确插入位置，时间复杂度约为 \$O(log n)\$。但是，为了在列表的中部插入元素，可能需要移动其他元素，以为新元素腾出空间，这种操作的时间复杂度为 \$O(n)\$。因此，将 n 个元素插入堆中的操作为 \$O(nlogn)\$。然而，如果从完整的列表开始，构建整个堆只需 \$O(n)\$。代码清单 6-22 给出了构建整个堆的代码。

代码清单6-22 根据元素列表构建堆
def buildHeap(self,alist):
    i = len(alist) // 2
    self.currentSize = len(alist)
    self.heapList = [0] + alist[:]
    while (i > 0):
        self.percDown(i)
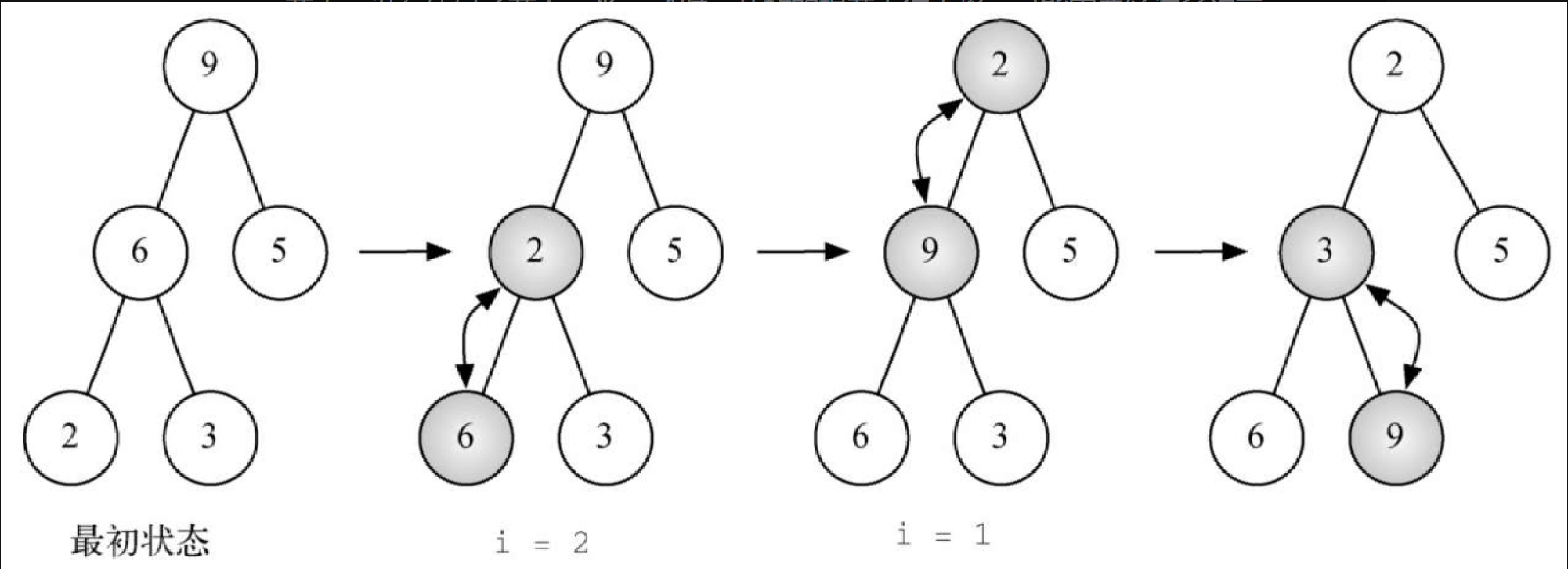
        i = i - 1

图6-18 展示了 buildHeap 方法进行的交换过程，它将各节点从最初状态移到各自的正确位置上。尽管从树的中间开始，向根的方向操作，但是 percDown 方法保证了最大的节点总是沿着树向下移动。在这棵完全二叉树中，超过中点的节点都是叶子节点，没有任何子节点。当 i = 1 时，从树的根节点往下移，可能需要经过多次交换。如你所见，9 先被移出根节点，然后 percDown 会沿着树检查子节点，以确保尽量将它往下移。在本例中，9 的第 2 次交换对象是 3。这样一来，9 就移到了树的底层，不需要再做交换了。比较一系列交换操作后的列表表示将有助于理解，如图 6-19 所示。

image 2023 12 13 18 57 04 540
Figure 5. 图6-18 根据列表[9, 6, 5, 2, 3]构建堆
image 2023 12 13 18 57 24 905
Figure 6. 图6-19 根据列表[9, 6, 5, 2, 3]构建堆

前面说过，构建堆的时间复杂度是 \$O(n)\$，这乍一听可能很难理解，证明过程超出了本书范畴。不过，要点在于，因子 \$log n\$ 是由树的高度决定的。在 buildHeap 的大部分工作中，树的高度不足 \$log n\$。

利用建堆的时间复杂度为 \$O(n)\$ 这一点，可以构造一个使用堆为列表排序的算法，使它的时间复杂度为 \$O(nlogn)\$。这个算法留作练习。