宽度优先搜索

词梯问题

我们从词梯问题开始学习图算法。考虑这样一个任务：将单词 FOOL 转换成 SAGE。在解决词梯问题时，必须每次只替换一个字母，并且每一步的结果都必须是一个单词，而不能是不存在的词。词梯问题由《爱丽丝梦游仙境》的作者刘易斯·卡罗尔于 1878 年提出。下面的单词转换序列是样例问题的一个解。

FOOL
POOL
POLL
POLE
PALE
SALE
SAGE

词梯问题有很多变体，例如在给定步数内完成转换，或者必须用到某个单词。在本节中，我们研究从起始单词转换到结束单词所需的最小步数。

由于本章的主题是图，因此我们自然会想到使用图算法来解决这个问题。以下是大致步骤：

用图表示单词之间的关系；
用一种名为宽度优先搜索的图算法找到从起始单词到结束单词的最短路径。

构建词梯图

第一个问题是如何用图来表示大的单词集合。如果两个单词的区别仅在于有一个不同的字母，就用一条边将它们相连。如果能创建这样一个图，那么其中的任意一条连接两个单词的路径就是词梯问题的一个解。图7-5 展示了一个小型图，可用于解决从 FOOL 到 SAGE 的词梯问题。注意，它是无向图，并且边没有权重。

Figure 1. 图7-5 用于解决词梯问题的小型图

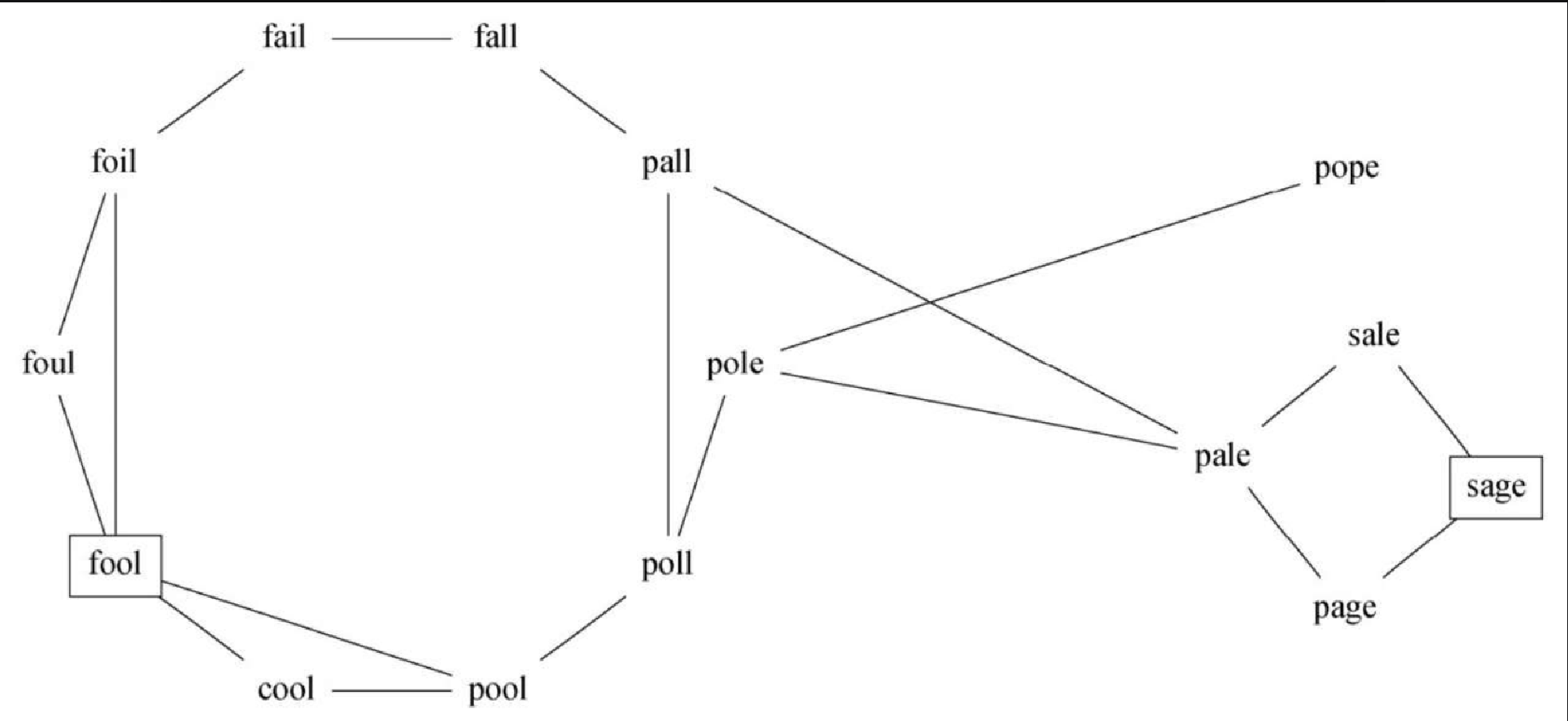
创建这个图有多种方式。假设有一个单词列表，其中每个单词的长度都相同。首先，为每个单词创建顶点。为了连接这些顶点，可以将每个单词与列表中的其他所有单词进行比较。如果两个单词只相差一个字母，就可以在图中创建一条边，将它们连接起来。对于只有少量单词的情况，这个算法还不错。但是，假设列表中有 5110 个单词，将一个单词与列表中的其他所有单词进行比较，时间复杂度为 \$O(n^2)\$。对于 5110 个单词来说，这意味着要进行 2600 多万次比较。

采用下述方法，可以更高效地构建这个关系图。假设有数目巨大的桶，每一个桶上都标有一个长度为4的单词，但是某一个字母被下划线代替。图7-6 展示了一些例子，如 POP_。当处理列表中的每一个单词时，将它与桶上的标签进行比较。使用下划线作为通配符，我们将 POPE 和 POPS 放入同一个桶中。一旦将所有单词都放入对应的桶中之后，我们就知道，同一个桶中的单词一定是相连的。

Figure 2. 图7-6 词桶示例

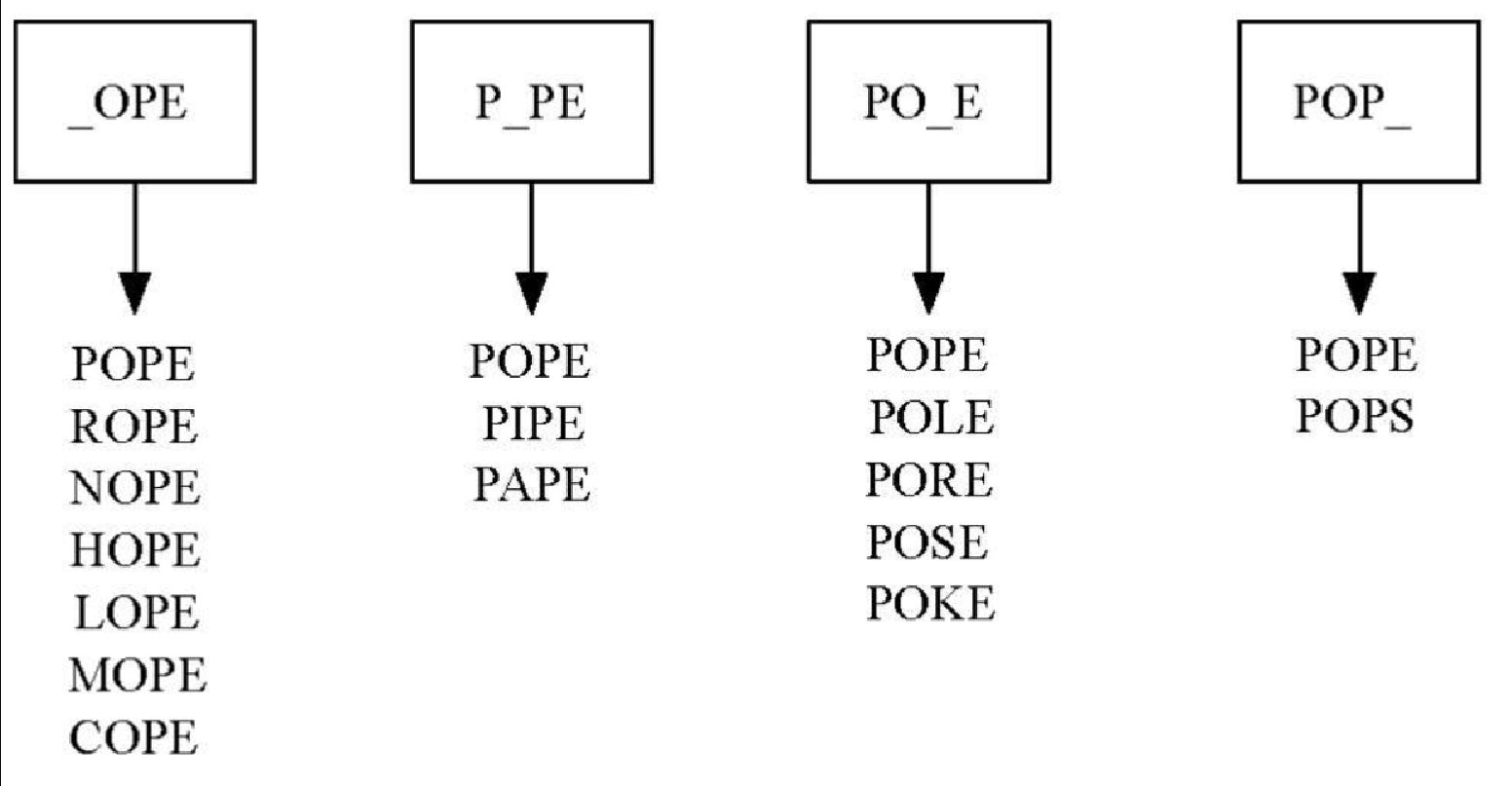
在 Python 中，可以通过字典来实现上述方法。字典的键就是桶上的标签，值就是对应的单词列表。一旦构建好字典，就能利用它来创建图。首先为每个单词创建顶点，然后在字典中对应同一个键的单词之间创建边。代码清单7-3 展示了构建图所需的 Python 代码。

代码清单7-3 为词梯问题构建单词关系图

from pythonds.graphs import Graph

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile,'r')
    # create buckets of words that differ by one letter
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
    # add vertices and edges for words in the same bucket
    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)
    return g

这是我们在本节中遇到的第一个实际的图问题，你可能会好奇这个图的稀疏程度如何。本例中的单词列表包含 5110 个单词。如果使用邻接矩阵表示，就会有 26112100 个单元格（5110 * 5110 = 26112100）。用 buildGraph 函数创建的图一共有 53286 条边。因此，只有 0.2% 的单元格被填充。这显然是一个非常稀疏的矩阵。

实现宽度优先搜索

完成图的构建之后，就可以编写能帮我们找到最短路径的图算法。我们使用的算法叫作宽度优先搜索（breadth first search，以下简称 BFS）。BFS 是最简单的图搜索算法之一，也是后续要介绍的其他重要图算法的原型。

给定图 G 和起点 s, BFS 通过边来访问在 G 中与 s 之间存在路径的顶点。BFS 的一个重要特性是，它会在访问完所有与 s 相距为 k 的顶点之后再去访问与 s 相距为 k+1 的顶点。为了理解这种搜索行为，可以想象 BFS 以每次生成一层的方式构建一棵树。它会在访问任意一个孙节点之前将起点的所有子节点都添加进来。

为了记录进度，BFS 会将顶点标记成白色、灰色或黑色。在构建时，所有顶点都被初始化成白色。白色代表该顶点没有被访问过。当顶点第一次被访问时，它就会被标记为灰色；当BFS完成对该顶点的访问之后，它就会被标记为黑色。这意味着一旦顶点变为黑色，就没有白色顶点与之相连。灰色顶点仍然可能与一些白色顶点相连，这意味着还有额外的顶点可以访问。

在代码清单7-4 中，BFS 使用7.3.3 节实现的邻接表来表示图。它还使用 Queue 来决定后续要访问的顶点，我们会了解到其重要性。

代码清单7-4 宽度优先搜索

from pythonds.graphs import Graph, Vertex
from pythonds.basic import Queue

def bfs(g,start):
  start.setDistance(0)
  start.setPred(None)
  vertQueue = Queue()
  vertQueue.enqueue(start)
  while (vertQueue.size() > 0):
    currentVert = vertQueue.dequeue()
    for nbr in currentVert.getConnections():
      if (nbr.getColor() == 'white'):
        nbr.setColor('gray')
        nbr.setDistance(currentVert.getDistance() + 1)
        nbr.setPred(currentVert)
        vertQueue.enqueue(nbr)
    currentVert.setColor('black')

除此以外，BFS 还使用了 Vertex 类的扩展版本。这个新的 Vertex 类新增了 3 个实例变量：distance、predecessor 和 color。每一个变量都有对应的 getter 方法和 setter 方法。扩展后的 Vertex 类被包含在 pythonds 包中。因为其中没有新的知识点，所以此处不展示这个类。

BFS 从起点 s 开始，将它标记为灰色，以表示正在访问它。另外两个变量，distance 和 predecessor，被分别初始化为 0 和 None。随后，start 被放入 Queue 中。下一步是系统化地访问位于队列头部的顶点。我们通过遍历邻接表来访问新的顶点。在访问每一个新顶点时，都会检查它的颜色。如果是白色，说明顶点没有被访问过，那么就执行以下 4 步。

将新的未访问顶点 nbr 标记成灰色。
将 nbr 的 predecessor 设置成当前顶点 currentVert。
将 nbr 的 distance 设置成到 currentVert 的 distance 加 1。
将 nbr 添加到队列的尾部。这样做为之后访问该顶点做好了准备。但是，要等到 currentVert 邻接表中的所有其他顶点都被访问之后才能访问该顶点。

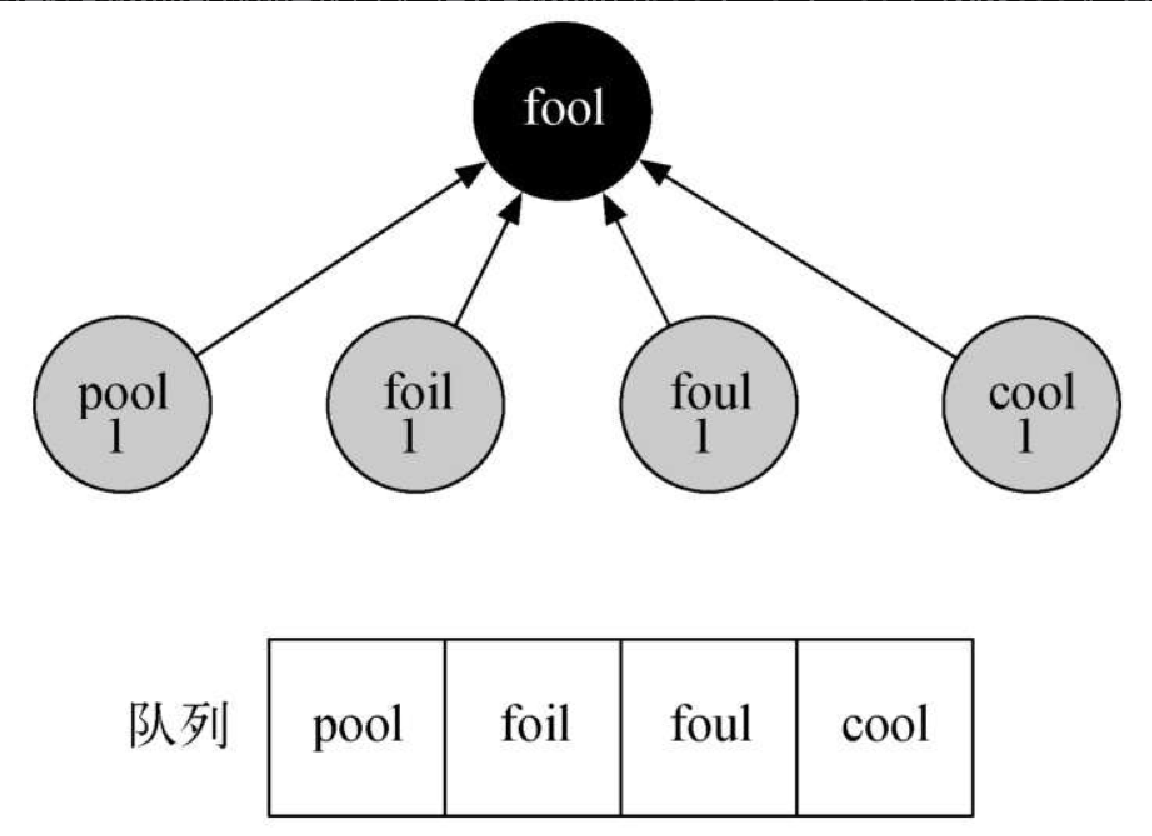
来看看 bfs 函数如何构建对应于图7-5 的宽度优先搜索树。从顶点 fool 开始，将所有与之相连的顶点都添加到树中。相邻的顶点有 pool、foil、foul，以及 cool。它们都被添加到队列中，作为之后要访问的顶点。图7-7 展示了正在构建中的树以及完成这一步之后的队列。

Figure 3. 图7-7 宽度优先搜索的第1步

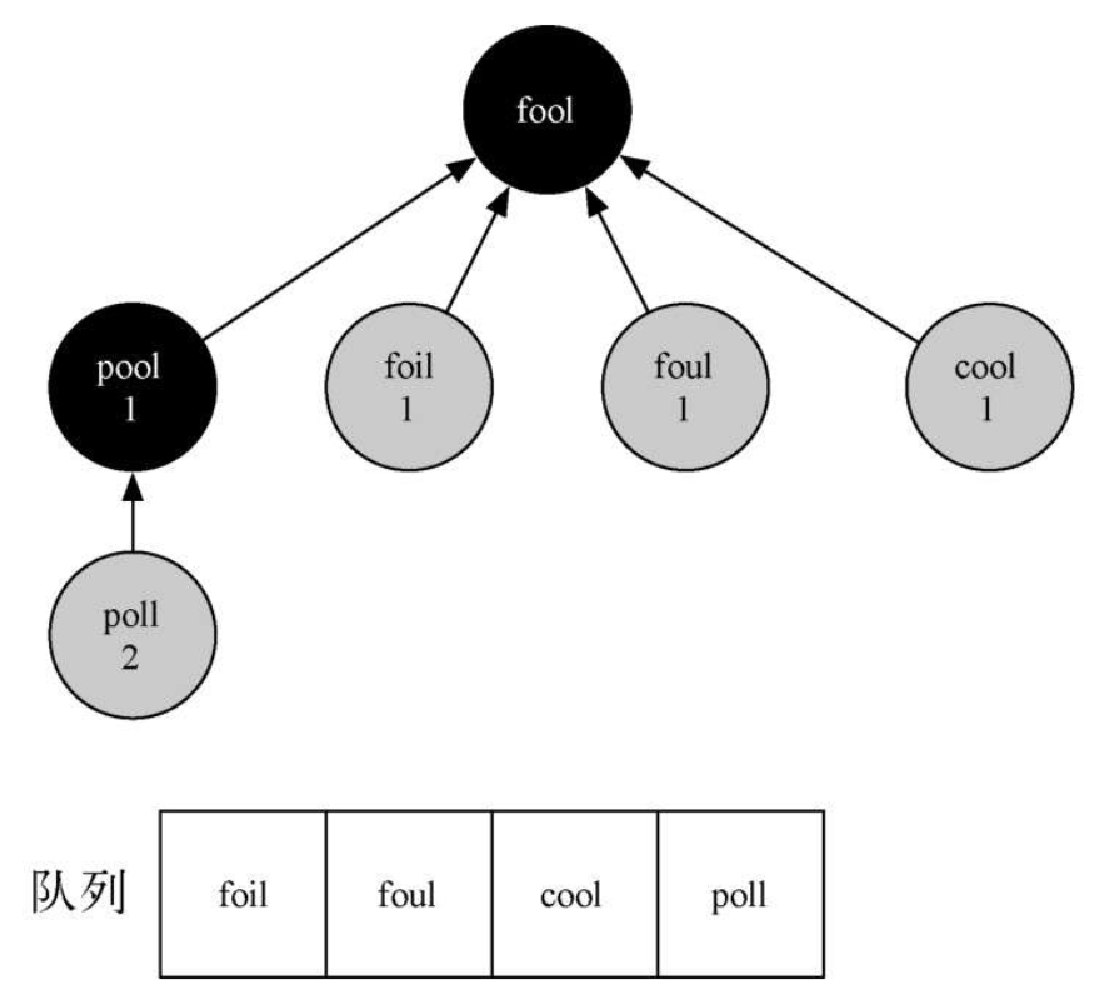
接下来，bfs 函数从队列头部移除下一个顶点（pool）并对它的邻接顶点重复之前的过程。但是，当检查 cool 的时候，bfs 函数发现它的颜色已经被标记为了灰色。这意味着从起点到 cool 有一条更短的路径，并且 cool 已经被添加到了队列中。图7-8 展示了树和队列的新状态。

Figure 4. 图7-8 宽度优先搜索的第2步

队列中的下一个顶点是 foil。唯一能添加的新顶点是 fail。当 bfs 函数继续处理队列时，后面的两个顶点都没有可供添加到队列和树中的新顶点。图7-9a 展示了树和队列在扩展了第 2 层之后的状态。

Figure 5. 图7-9 构建宽度优先搜索树

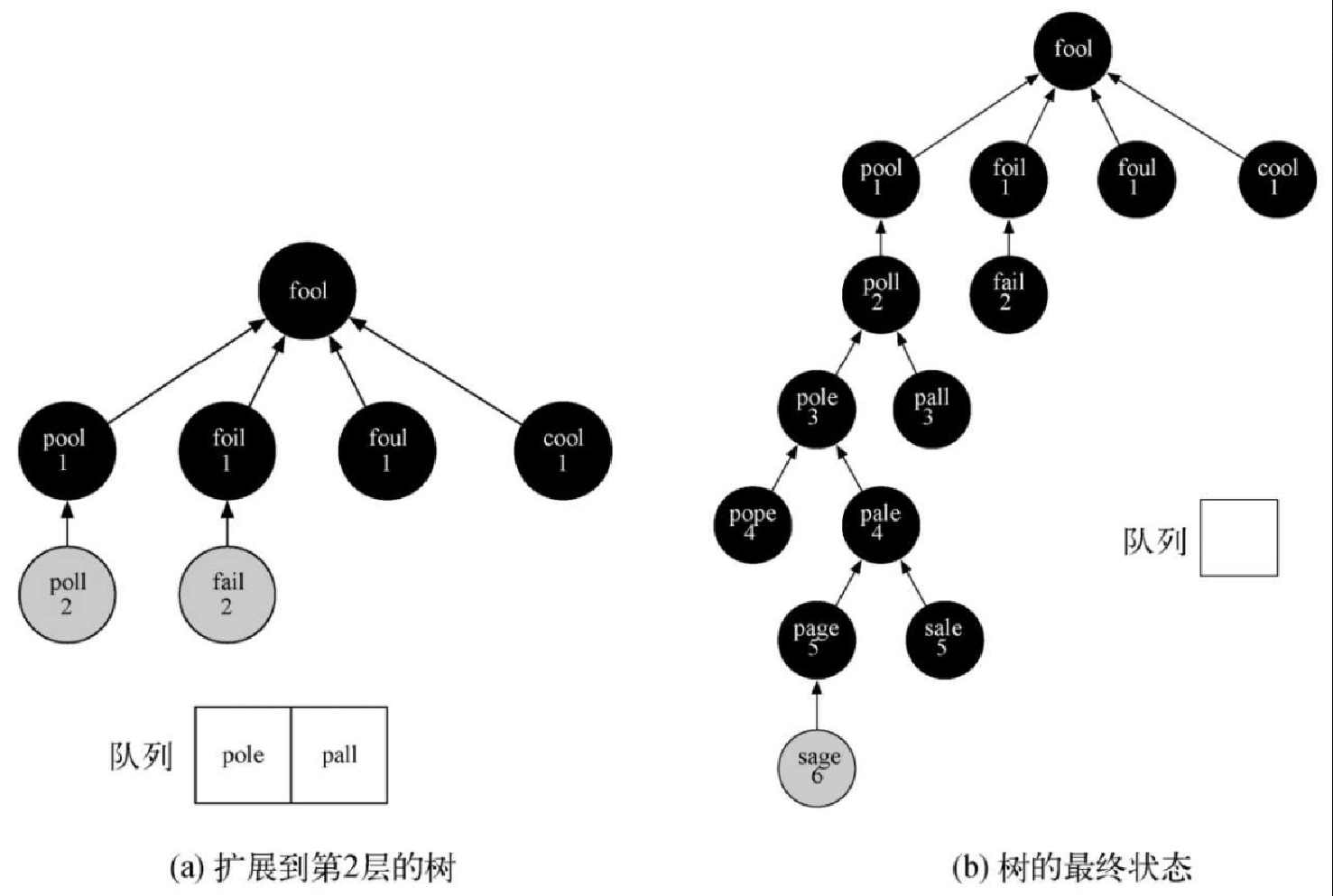
请继续研究 bfs 函数，直到能够理解其原理为止。图7-9b 展示了访问完图7-5 中所有顶点之后的宽度优先搜索树。非常神奇的一点是，我们不仅解决了一开始提出的从 FOOL 转换成 SAGE 的问题，同时也解决了许多其他问题。可以从宽度优先搜索树中的任意节点开始，跟随 predecessor 回溯到根节点，以此来找到任意单词到 fool 的最短词梯。代码清单7-5 中的函数展示了如何通过回溯 predecessor 链来打印整个词梯。

代码清单7-5 回溯宽度优先搜索树

def traverse(y):
    x = y
    while (x.getPred()):
        print(x.getId())
        x = x.getPred()
    print(x.getId())

traverse(g.getVertex('sage'))

分析宽度优先搜索

在学习其他图算法之前，让我们先分析 BFS 的性能。在代码清单7-4 中，第 8 行的 while 循环对于 |V| 中的任一顶点最多只执行一次。这是因为只有白色顶点才能被访问并添加到队列中。这使得 while 循环的时间复杂度是\$O(V)\$。至于嵌套在 while 循环中的 for 循环（第 10 行），它对每一条边都最多只会执行一次。原因是，每一个顶点最多只会出列一次，并且我们只有在顶点 u 出列时才会访问从 u 到 v 的边。这使得 for 循环的时间复杂度为 \$O(E)\$。因此，两个循环总的时间复杂度就是 \$O(V+E)\$。

进行宽度优先搜索只是整个任务的一部分，从起点一直找到终点则是任务的另一部分。这部分的最坏情况是整个图是一条长链。在这种情况下，遍历所有顶点的时间复杂度是 \$O(V)\$。正常情况下，时间复杂度等于 \$O(V)\$ 乘以某个小数，但是我们仍然用 \$O(V)\$ 来表示。

最后，对于本节的问题来说，还需要时间构建初始图。我们将 buildGraph 函数的时间复杂度分析留作练习。