图的抽象数据类型

图的抽象数据类型由下列方法定义。

Graph() 新建一个空图。
addVertex(vert) 向图中添加一个顶点实例。
addEdge(fromVert, toVert) 向图中添加一条有向边，用于连接顶点 fromVert 和 toVert。
addEdge(fromVert, toVert, weight) 向图中添加一条带权重 weight 的有向边，用于连接顶点 fromVert 和 toVert。
getVertex(vertKey) 在图中找到名为 vertKey 的顶点。
getVertices() 以列表形式返回图中所有顶点。
in 通过 vertex in graph 这样的语句，在顶点存在时返回 True，否则返回 False。

根据图的正式定义，可以通过多种方式在 Python 中实现图的抽象数据类型。你会看到，在使用不同的表达方式来实现图的抽象数据类型时，需要做很多取舍。有两种非常著名的图实现，它们分别是邻接矩阵和邻接表。本节会解释这两种实现，并且用 Python 类来实现邻接表。

邻接矩阵

要实现图，最简单的方式就是使用二维矩阵。在矩阵实现中，每一行和每一列都表示图中的一个顶点。第 v 行和第 w 列交叉的格子中的值表示从顶点 v 到顶点 w 的边的权重。如果两个顶点被一条边连接起来，就称它们是相邻的。图7-3 展示了图7-2 对应的邻接矩阵。格子中的值表示从顶点 v 到顶点 w 的边的权重。

Figure 1. 图7-3 邻接矩阵示例

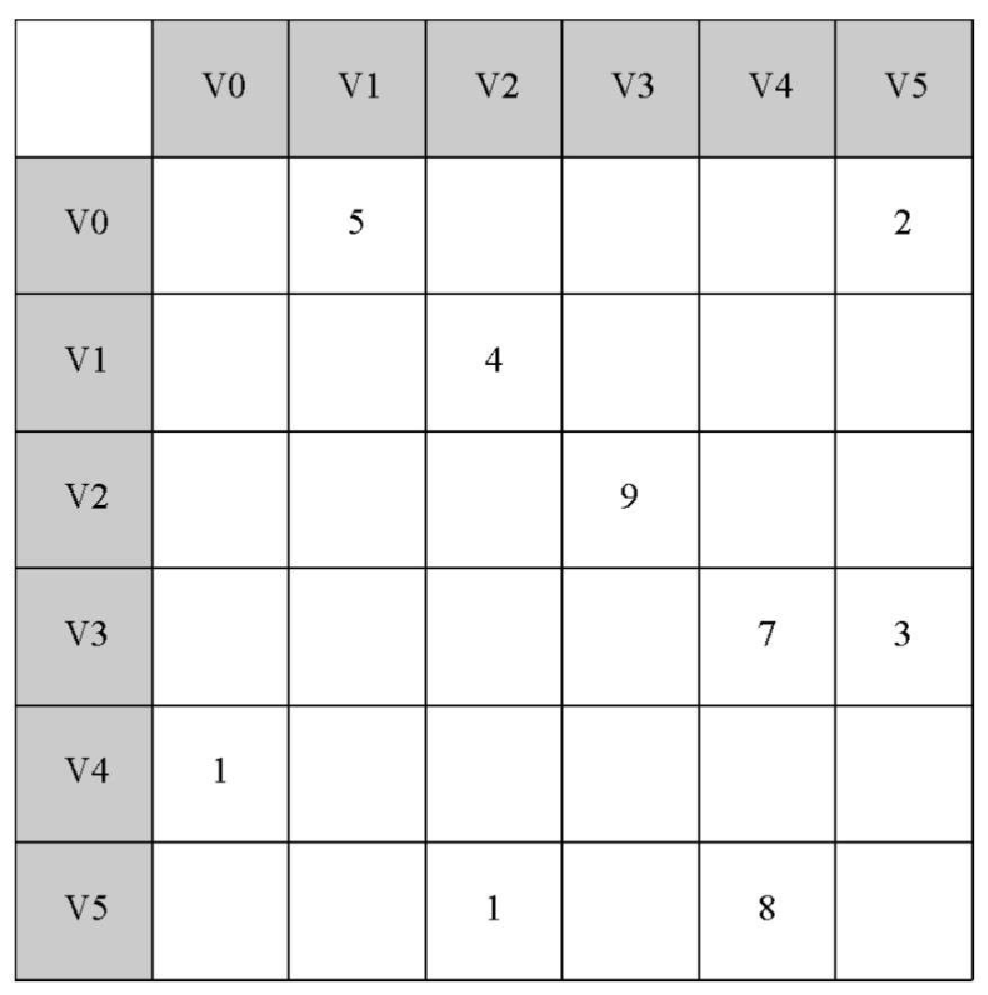
邻接矩阵的优点是简单。对于小图来说，邻接矩阵可以清晰地展示哪些顶点是相连的。但是，图7-3 中的绝大多数单元格是空的，我们称这种矩阵是 “稀疏” 的。对于存储稀疏数据来说，矩阵并不高效。事实上，要在 Python 中创建如图7-3 所示的矩阵结构并不容易。邻接矩阵适用于表示有很多条边的图。但是，“很多条边” 具体是什么意思呢？要填满矩阵，共需要多少条边？由于每一行和每一列对应图中的每一个顶点，因此填满矩阵共需要 |V|² 条边。当每一个顶点都与其他所有顶点相连时，矩阵就被填满了。在现实世界中，很少有问题能够达到这种连接度。本章所探讨的问题都会用到稀疏连接的图。

邻接表

为了实现稀疏连接的图，更高效的方式是使用邻接表。在邻接表实现中，我们为图对象的所有顶点保存一个主列表，同时为每一个顶点对象都维护一个列表，其中记录了与它相连的顶点。在对 Vertex 类的实现中，我们使用字典（而不是列表），字典的键是顶点，值是权重。图7-4 展示了图7-2 所对应的邻接表。

Figure 2. 图7-4 邻接表示例

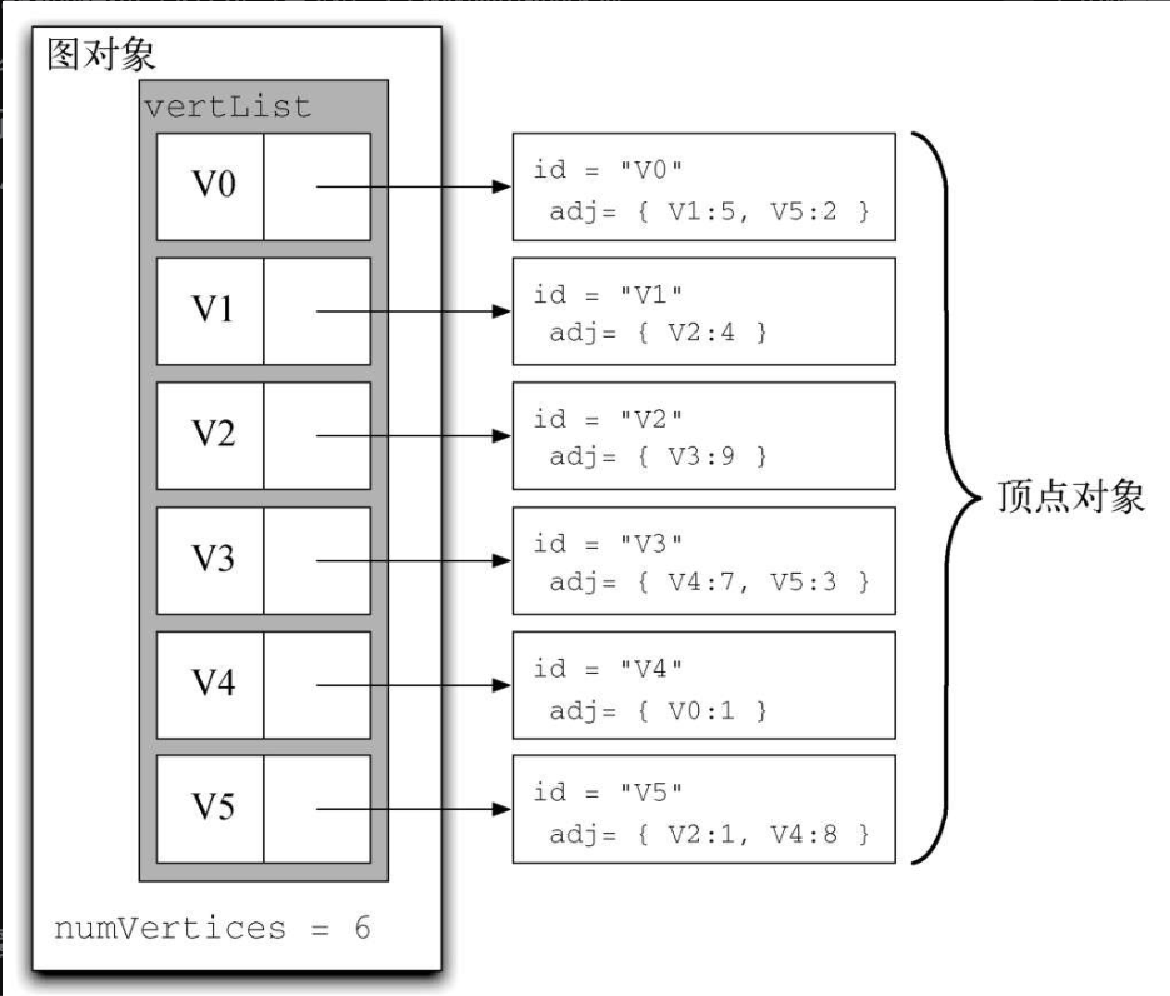
邻接表的优点是能够紧凑地表示稀疏图。此外，邻接表也有助于方便地找到与某一个顶点相连的其他所有顶点。

实现

在 Python 中，通过字典可以轻松地实现邻接表。我们要创建两个类：Graph 类存储包含所有顶点的主列表，Vertex 类表示图中的每一个顶点。

Vertex 使用字典 connectedTo 来记录与其相连的顶点，以及每一条边的权重。代码清单7-1 展示了 Vertex 类的实现，其构造方法简单地初始化 id（它通常是一个字符串），以及字典 connectedTo。addNeighbor 方法添加从一个顶点到另一个的连接。getConnections 方法返回邻接表中的所有顶点，由 connectedTo 来表示。getWeight 方法返回从当前顶点到以参数传入的顶点之间的边的权重。

代码清单7-1 Vertex类

class Vertex:
    def __init__(self,key):
        self.id = key
        self.connectedTo = {}

    def addNeighbor(self,nbr,weight=0):
        self.connectedTo[nbr] = weight

    def __str__(self):
        return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])

    def getConnections(self):
        return self.connectedTo.keys()

    def getId(self):
        return self.id

    def getWeight(self,nbr):
        return self.connectedTo[nbr]python

Graph 类的实现如代码清单7-2 所示，其中包含一个将顶点名映射到顶点对象的字典。在图7-4 中，该字典对象由灰色方块表示。Graph 类也提供了向图中添加顶点和连接不同顶点的方法。getVertices 方法返回图中所有顶点的名字。此外，我们还实现了 __iter__ 方法，从而使遍历图中的所有顶点对象更加方便。总之，这两个方法使我们能够根据顶点名或者顶点对象本身遍历图中的所有顶点。

代码清单7-2 Graph类

class Graph:
    def __init__(self):
        self.vertList = {}
        self.numVertices = 0

    def addVertex(self,key):
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)
        self.vertList[key] = newVertex
        return newVertex

    def getVertex(self,n):
        if n in self.vertList:
            return self.vertList[n]
        else:
            return None

    def __contains__(self,n):
        return n in self.vertList

    def addEdge(self,f,t,weight=0):
        if f not in self.vertList:
            nv = self.addVertex(f)
        if t not in self.vertList:
            nv = self.addVertex(t)
        self.vertList[f].addNeighbor(self.vertList[t], weight)

    def getVertices(self):
        return self.vertList.keys()

    def __iter__(self):
        return iter(self.vertList.values())python

下面的 Python 会话使用 Graph 类和 Vertex 类创建了如图7-2 所示的图。首先创建 6 个顶点，依次编号为 0～5。然后打印顶点字典。注意，对每一个键，我们都创建了一个 Vertex 实例。接着，添加将顶点连接起来的边。最后，用一个嵌套循环验证图中的每一条边都已被正确存储。请按照图 7-2 的内容检查会话的最终结果。

>>> g = Graph()
>>> for i in range(6):
...     g.addVertex(i)
>>> g.vertList
{0: <adjGraph.Vertex instance at 0x41e18>,
  1: <adjGraph.Vertex instance at 0x7f2b0>,
  2: <adjGraph.Vertex instance at 0x7f288>,
  3: <adjGraph.Vertex instance at 0x7f350>,
  4: <adjGraph.Vertex instance at 0x7f328>,
  5: <adjGraph.Vertex instance at 0x7f300>}
>>> g.addEdge(0, 1, 5)
>>> g.addEdge(0, 5, 2)
>>> g.addEdge(1, 2, 4)
>>> g.addEdge(2, 3, 9)
>>> g.addEdge(3, 4, 7)
>>> g.addEdge(3, 5, 3)
>>> g.addEdge(4, 0, 1)
>>> g.addEdge(5, 4, 8)
>>> g.addEdge(5, 2, 1)
>>> for v in g:
...     for w in v.getConnections():
...          print("( %s , %s )" % (v.getId(), w.getId()))
...
(0, 5)
(0, 1)
(1, 2)
(2, 3)
(3, 4)
(3, 5)
(4, 0)
(5, 4)
(5, 2)python