复习树:量化图片

图片是互联网上十分常见的元素，其常见程度仅次于文字。不过，如果每张广告图片都占据 196560 字节，那么互联网会慢很多。实际上，横幅广告图片只需约 14246 字节，即原存储空间的 7.2%。这些数字从何而来？怎么才能如此显著地节省空间？答案就在本节中。

数字图像概述

一幅数字图像由数以千计的像素组成。像素排列成矩阵，形成图像。图像中的每个像素代表一个特定的颜色，由三原色混合而成：红、绿、蓝。图8-14 简单地展示了像素如何排列成图像。

Figure 1. 图8-14 简单的图

在物理世界中，不同颜色之间的过渡是连续的。就像利用浮点数近似表示实数一样，计算机也必须近似表示图像中的颜色。对于每种三原色，人眼可以区分 200 种不同的层次，总共约 800 万种颜色。在实践中，我们使用 1 字节（8 位）表示像素的每个颜色构成。8 位可以表示每种三原色的 256 种层次，所以每个像素可能有约 1670 万种颜色。海量的颜色选择有助于艺术家和设计师创造出细节丰富的图片，但也有坏处，那就是图片文件的大小会迅速膨胀。举例来说，一张由百万像素相机拍出来的照片，会占据 3 兆字节的内存空间。

Python 使用元组列表来表示图片，元组由 3 个取值范围是 0～255 的数字构成，它们分别代表红、绿、蓝。在 C++ 和 Java 等语言中，图片表示为二维数组。以图8-14 为例，该图的头两行表示如下：

im = [[(255, 255, 255), (255, 255, 255), (255, 255, 255), (12, 28, 255), (12, 28, 255),
(255, 255, 255), (255, 255, 255), (255, 255, 255)], [(255, 255, 255), (255, 255, 255),
(12, 28, 255), (255, 255, 255), (255, 255, 255), (12, 28, 255), (255, 255, 255), (255,255, 255)],
...]

白色表示为 (255, 255, 255)，蓝色表示为 (12, 28, 255)。使用列表索引可以查看图片中任一像素的颜色，如下所示：

>>> im[3][2]
(255, 18, 39)

有了这种图片表示方法，就不难将图片存为文件——只需为每个像素写一个元组即可。可以先确定像素的行数和列数，然后每行写 3 个整数。实践中，PIL（Python Image Library）提供了更强大的图片类。我们可以通过 getPixelcol, row 和 setPixel((col, row), colorTuple) 读取和设置像素。注意，参数对应的是坐标，而不是行数和列数。

量化图片

有很多方法可以节省图片的存储空间，最简单的就是减少所用颜色的种类。颜色越少，红、绿、蓝的位数就越少，所需的存储空间也将随之减少。实际上，最流行的一种用于互联网的图片格式只使用了 256 种颜色。这意味着将所需的存储空间从每像素3字节降到了每像素 1 字节。

你可能会问，如何将颜色从 1670 万种降到 256 种呢？答案就是量化。要理解量化，我们将颜色想象成一个三维空间。x 轴代表红色，y 轴代表绿色，z 轴则代表蓝色。每种颜色都可以看作这个空间中的一个点。我们将由所有颜色构成的空间想象成一个 256×256×256 的立方体。越靠近 (0, 0, 0) 处，颜色越黑、越暗；越靠近 (255,255, 255) 处，颜色则越白、越亮；靠近 (255, 0, 0) 处的颜色偏红，依此类推。

最简单的量化过程是将 256×256×256 的立方体转化成 8×8×8 的立方体。虽然体积不变，但原立方体中的多种颜色在新立方体中成了一种，如图8-15 所示。

Figure 2. 图8-15 颜色量化

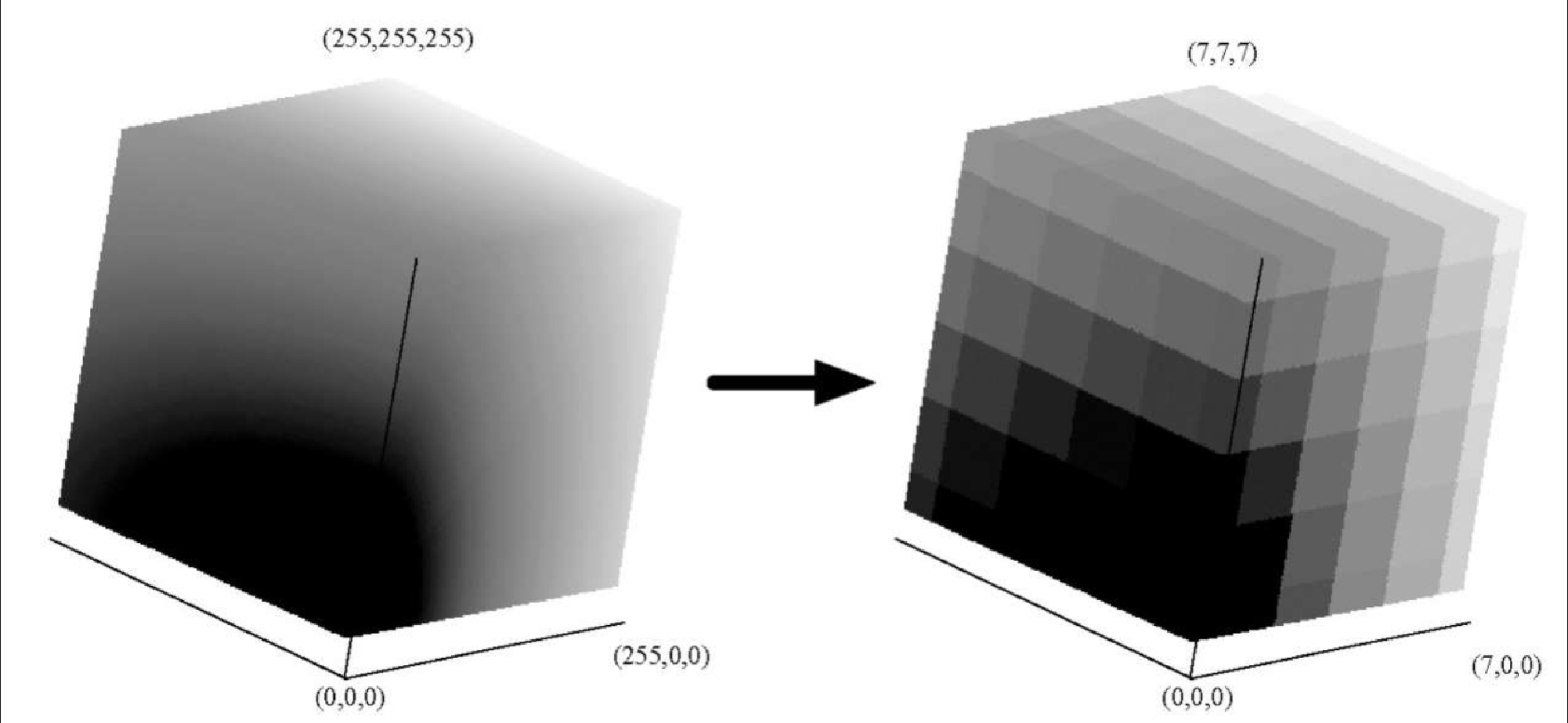
可以用 Python 实现上述颜色量化算法，如代码清单8-21 所示。simpleQuant 将每个像素的 256 位表示的颜色映射到像素中心处的颜色。这一步使用 Python 的整除很容易做到。在 simpleQuant 中，红色维度上有 7 个值，绿色和蓝色维度上有 6 个值。

代码清单8-21 简单的图片量化算法

import sys
import os
import Image

def simpleQuant():
    im = Image.open('bubbles.jpg')
    w, h = im.size
    for row in range(h):
        for col in range(w):
            r, g, b = im.getpixel((col, row))
            r = r // 36 * 36
            g = g // 42 * 42
            b = b // 42 * 42
            im.putpixel((col, row), (r, g, b))
    im.show()

图8-16 是量化前后的对比效果。当然，这些图在印刷版中变成了灰度图。如果看彩图，会发现量化后的图片损失了不少细节。草地几乎损失了所有细节，只是一片绿，人的肤色也简化成了两片棕色阴影。

Figure 3. 图8-16 使用简单的图片量化算法的前后对比效果

使用八叉树改进量化算法

simpleQuant 的问题在于，大部分图片中的颜色不是均匀分布的。很多颜色可能没有出现在图片中，所以立方体中对应的部分并没有用到。在量化后的图片中分配没用到的颜色是浪费行为。图8-17 展示了示例图片中的颜色分布。注意，只用了立方体的一小部分空间。

Figure 4. 图8-17 示例图片用到的颜色

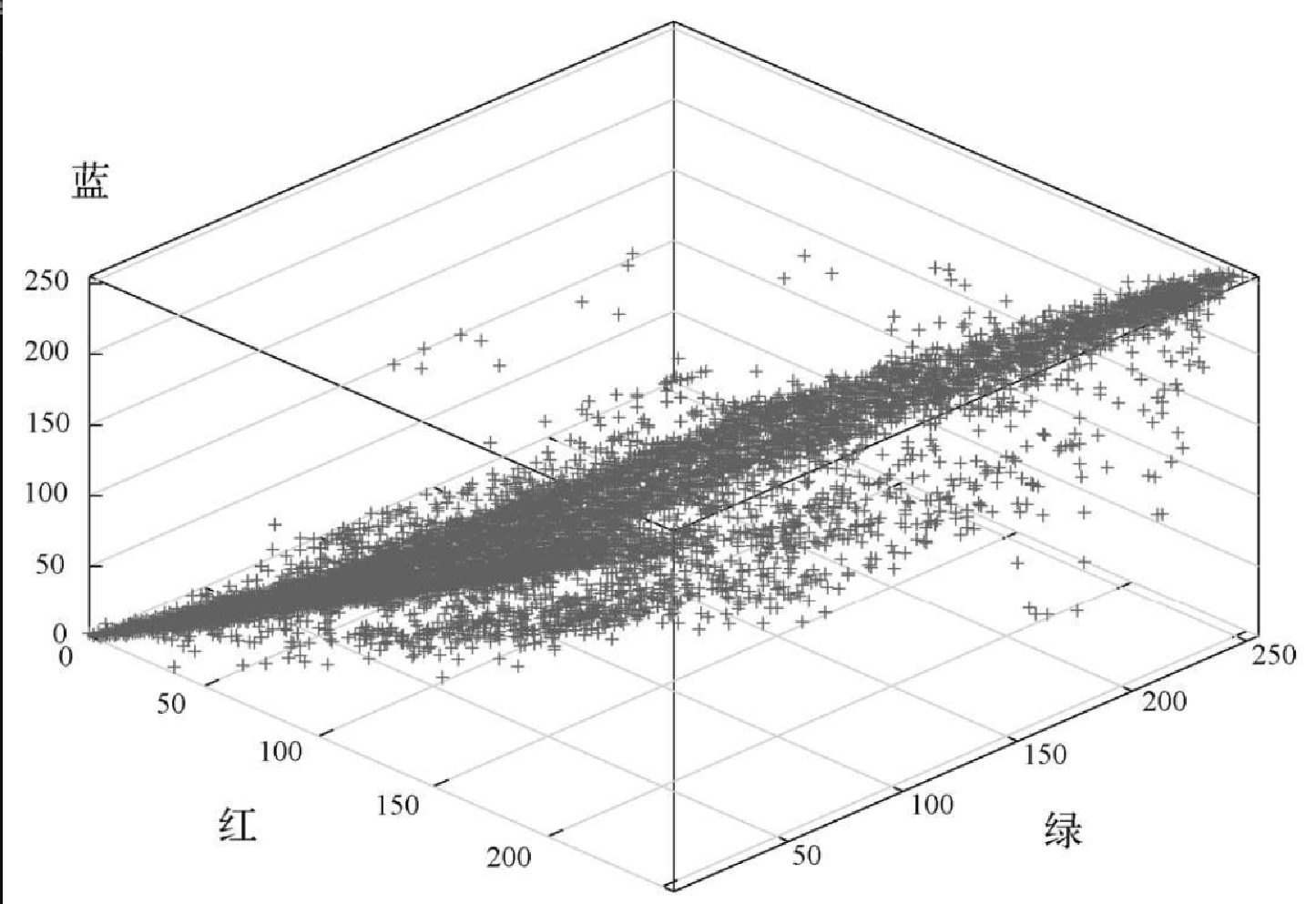
为了更好地量化图片，就要找到更好的方法，选出表示图片时用到的颜色集合。有多种算法可用于切分立方体，以更好地使用颜色。本节将介绍基于八叉树的算法。八叉树类似于二叉树，但每个节点有 8 个子节点。下面是 OctTree 抽象数据类型将实现的接口。

OctTree() 新建一棵空的八叉树。
insert(r, g, b) 往八叉树中插入一个节点，以红、绿、蓝的值为键。
find(r, g, b) 以红、绿、蓝的值为搜索键，查找一个节点，或与其最相似的节点。
reduce(n) 缩小八叉树，使其有 n 个或更少的叶子节点。

OctTree 通过如下方式切分颜色立方体。

OctTree 的根代表整个立方体。
OctTree 的第二层代表每个维度（包括 x 轴、y 轴和 z 轴）上的一个切片，将立方体等分成 8 块。
下一层将 8 个子块中的每一块再等分成 8 块，即共有 64 块。注意，父节点代表的方块包含其子节点代表的所有子块。沿着路径往下，子块始终位于父节点所规定的界限内，但会越来越具体。
八叉树的第 8 层代表所有颜色（约有 1670 万种）。

了解如何用八叉树表示颜色立方体之后，你可能认为这不过又是一种等分立方体的方法。没错，不过八叉树是分级的，我们可以利用其层级，用大立方体表示未使用的颜色，用小立方体表示常用颜色。以下大致介绍如何使用 OctTree 更好地选择图片的颜色子集。

针对图片中的每个像素，执行以下操作：
- 在 OctTree 中查找该像素的颜色，这个颜色应该是位于第 8 层的一个叶子节点；
- 如果没找到，就在第 8 层创建一个叶子节点（可能还需要在叶子节点之上创建一些内部节点）；
- 如果找到了，将叶子节点中的计数器加 1，以记录这个颜色用于多少个像素。
重复以下步骤，直到叶子节点的数目小于或等于颜色的目标数目：
- 找到用得最少的叶子节点；
- 合并该叶子节点及其所有兄弟节点，从而形成一个新的叶子节点。
剩余的叶子节点形成图片的颜色集。
若要将初始的颜色映射为量化后的值，只需沿着树向下搜索到叶子节点，然后返回叶子节点存储的颜色值。

可以将上述思路实现为 Python 函数 buildAndDisplay()，以读取、量化和展示图片，如代码清单8-22 所示。

代码清单8-22 使用八叉树构建和展示量化后的图片

def buildAndDisplay():
    im = Image.open('bubbles.jpg')
    w,h = im.size
    ot = OctTree()
    for row in range(0, h):
        for col in range(0, w):
            r, g, b = im.getpixel((col, row))
            ot.insert(r, g, b)

    ot.reduce(256)  # 减为 256 种颜色

    for row in range(0, h):
        for col in range(0, w):
            r, g, b = im.getpixel((col, row))
            nr, ng, nb = ot.find(r, g, b)
            im.putpixel((col, row), (nr, ng, nb))  # 用量化后的新值替换像素

    im.show()

这个函数遵循了前面描述的基本步骤。首先，第 5～8 行的循环读取每个像素，并将其加到八叉树中。第 8 行往八叉树中插入像素。减少叶子节点的工作由第 10 行的 reduce 方法完成。第 15 行使用 find 方法，在缩小后的八叉树中搜索颜色，并更新图片。

本例使用了 PIL 库中的 4 个简单函数：Image.open 打开已有的图片文件，getpixel 读取像素，putpixel 写入像素，show 在屏幕上展示结果。

现在来看看 OctTree 类及其关键方法。请注意，这里其实有两个类。OctTree 类用于 buildAndDisplay 函数，但其实只是用了它的一个实例。第二个类是 OctTree 类内部定义的 otNode。这种定义于另一个类内部的类称作内部类。之所以在 OctTree 类的内部定义 otNode，是因为 OctTree 的每个节点都需要访问一些存储于 OctTree 类实例中的信息。还有一个原因是，没有任何在 OctTree 类之外使用 otNode 的必要。otNode 是 OctTree 私有的，别人不需要了解它的实现细节。这是软件工程中的良好实践，称作 “信息隐藏”。

buildAndDisplay 用到的所有函数都在 OctTree 类中定义。代码清单 8-23～代码清单8-27 展示了 OctTree 类的实现。注意，构造方法首先将根节点初始化为 None，然后设置了所有节点都可能访问的 3 个重要属性：maxLevel、numLeaves 和 leafList。maxLevel 属性限制了树的总体深度，本例将它初始化为 5。我们仅略微改进量化算法，以忽略颜色信息中的两个最低有效位。即便如此，也能让树总体上小得多，并且也不会降低最终图片的质量。numLeaves 和 leafList 记录叶子节点的数目，从而使我们能直接访问叶子节点，而不用沿着树遍历。你很快就能看到这样做的重要性。

代码清单8-23 OctTree类

class OctTree:
    def __init__(self):
        self.root = None
        self.maxLevel = 5
        self.numLeaves = 0
        self.leafList = []

    def insert(self, r, g, b):
        if not self.root:
            self.root = self.otNode(outer=self)
            self.root.insert(r, g, b, 0, self)

    def find(self, r, g, b):
        if self.root:
            return self.root.find(r, g, b, 0)

    def reduce(self, maxCubes):
        while len(self.leafList) > maxCubes:
            smallest = self.findMinCube()
            smallest.parent.merge()
            self.leafList.append(smallest.parent)
            self.numLeaves = self.numLeaves + 1

    def findMinCube(self):
        minCount = sys.maxint
        maxLev = 0
        minCube = None
        for i in self.leafList:
            if i.count <= minCount and i.level >= maxLev:
                minCube = i
                minCount = i.count
                maxLev = i.level
        return minCube

八叉树的 insert 方法和 find 方法与第 6 章中的类似。先检查根节点是否存在，然后调用根节点相应的方法。注意，这两个方法都使用红、绿、蓝标识树中的节点。

在代码清单8-23 中，第 17 行定义 reduce 方法。这个方法一直循环，直到叶子列表中的节点数目小于在最终图片中要保留的颜色总数（由参数 maxCubes 定义）。reduce 使用辅助函数 findMinCube 找到 OctTree 中引用数最少的节点，然后将该节点与其所有的兄弟节点合并成一个节点（参见第 20 行）。findMinCube 方法通过 leafList 和一个查找最小值的循环模式实现。当叶子节点很多时——可以达到 1670 万个——这种做法的效率极低。在章末的练习中，你需要修改 OctTree，以提升 findMinCube 的效率。

现在来看 OctTree 中节点的类定义，如代码清单8-24 所示。otNode 类的构造方法有 3 个可选参数。参数让 OctTree 方法可以在多种环境下构造新节点。和在二叉搜索树中一样，我们显式记录节点的父节点。节点的层数表明它在树中的深度。在这 3 个参数中，最有趣的就是 outer，这是指向创建这个节点的 OctTree 实例的引用。和 self 一样，outer 允许 otNode 实例访问 OctTree 实例的属性。

关于 OctTree 中的每个节点，我们要记住的其他属性包括引用计数 count 和红、绿、蓝等颜色构成。在 insert 方法中，只有叶子节点有 red、green、blue 和 count 的值。并且，每个节点最多可以有 8 个子节点，所以我们初始化一个有 8 个引用的列表，以记录它们。二叉树只有左右两个子节点，八叉树则有 8 个子节点，编号分别为 0～7。

代码清单8-24 otNode类及其构造方法

class otNode:
    def __init__(self, parent=None, level=0, outer=None):
        self.red = 0
        self.green = 0
        self.blue = 0
        self.count = 0
        self.parent = parent
        self.level = level
        self.oTree = outer
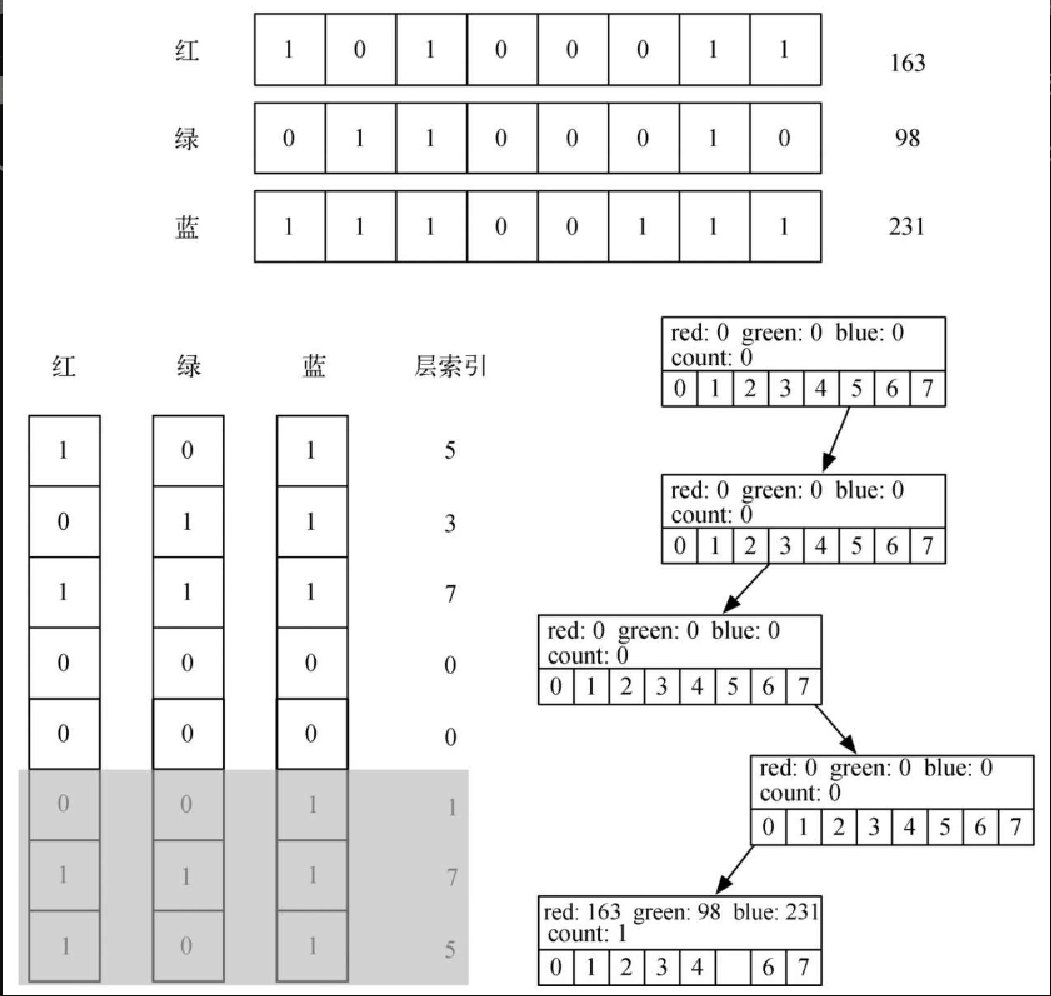
        self.children = [None] * 8

现在来看 OctTree 中真正有趣的部分。代码清单8-25 是往 OctTree 中插入新节点的 Python 代码。要解决的第一个问题是如何找出新节点在树中的位置。二叉树中的规则是，键比父节点小的节点都在左子树，键比父节点大的都在右子树。但如果每个节点都有 8 个子节点，就没这么简单了。另外，在处理颜色时，不容易说清楚每个节点的键该是什么。OctTree 使用三原色组成的信息。图8-18 展示了如何使用红、绿、蓝的值计算新节点在每一层的位置，相应的代码在代码清单8-25 中的第 18 行。

Figure 5. 图8-18 计算插入节点的位置

代码清单8-25 insert方法

def insert(self, r, g, b, level, outer):
    if level < self.oTree.maxLevel:
        idx = self.computeIndex(r, g, b, level)
        if self.children[idx] == None:
            self.children[idx] = outer.otNode(parent=self,
                                              level=level + 1,
                                              outer=outer)
        self.children[idx].insert(r, g, b, level + 1, outer)
    else:
        if self.count == 0:
            self.oTree.numLeaves = self.oTree.numLeaves + 1
            self.oTree.leafList.append(self)
        self.red += r
        self.green += g
        self.blue += b
        self.count = self.count + 1

def computeIndex(self, r, g, b, level):
    shift = 8 - level
    rc = r >> shift - 2 & 0x4
    gc = g >> shift - 1 & 0x2
    bc = b >> shift & 0x1
    return (rc | gc | bc)

插入位置的计算结合了红、绿、蓝成分的信息，从树根出发，以最高有效位开始。图8-18 给出了红（163）、绿（98）、蓝（231）各自的二进制表示。从每个颜色的最高有效位开始，本例中分别是1、0和1，放在一起得到二进制数 101，对应十进制数 5。在代码清单8-25 中，第 18 行的 computeIndex 方法进行了这样的二进制操作。

你可能不熟悉 computeIndex 使用的运算符。>> 是右移操作，& 是位运算中的 and, | 则是位运算中的 or。位运算和条件判断中的逻辑运算一样，只不过它们操作的对象是数字的位。移动操作将比特向右移动 n 位，左边用 0 填充，右边超出的部分直接舍去。

计算出当前层的索引后，进入子树。在图8-18 的例子中，我们循着 children 数组第 5 个位置上的链接往下。如果位置 5 没有节点，就新建一个。往下遍历，直到抵达 maxLevel 层。在这一层停止搜索，存储数据。注意，不是覆盖叶子节点中的数据，而是加到各颜色成分上，并增加引用计数。这样做可以计算颜色立方体中当前节点之下的颜色的平均值。这么一来，OctTree 中的叶子节点就可以表示立方体中一系列相似的颜色。

find 方法（如代码清单8-26 所示）使用和 insert 方法相同的索引计算方法，遍历八叉树，以搜索匹配红、绿、蓝成分的节点。find 方法有 3 种退出情形。

到达 maxLevel 层，返回叶子节点中颜色信息的平均值（参见第 15 行）。
在小于 maxLevel 的层上找到一个叶子节点（参见第 9 行）。稍后会介绍，只有在精简树之后，才会出现这种情形。
路径导向不存在的子树，这是个错误。

代码清单8-26 find方法

def find(self, r, g, b, level):
    if level < self.oTree.maxLevel:
        idx = self.computeIndex(r, g, b, level)
        if self.children[idx]:
            return self.children[idx].find(r, g, b, level + 1)
        elif self.count > 0:
            return ((self.red // self.count,
                 self.green // self.count,
                 self.blue // self.count))
        else:
            print("error: No leaf node for this color")
    else:
        return ((self.red // self.count,
             self.green // self.count,
             self.blue // self.count))

otNode 类的最后一个方法是 merge，如代码清单8-27 所示。merge 方法允许父节点纳入所有的子节点，从而形成一个叶子节点。如果还记得 OctTree 的每个父立方体完全包含所有子立方体，你就能明白。合并一组兄弟节点时，相当于是给它们各自代表的颜色计算加权平均值。既然兄弟节点在颜色立方体中相互离得很近，那么这个平均值就可以很好地代表它们。图8-19 描绘了合并兄弟节点的过程。

Figure 6. 图8-19 合并八叉树中的4个叶子节点

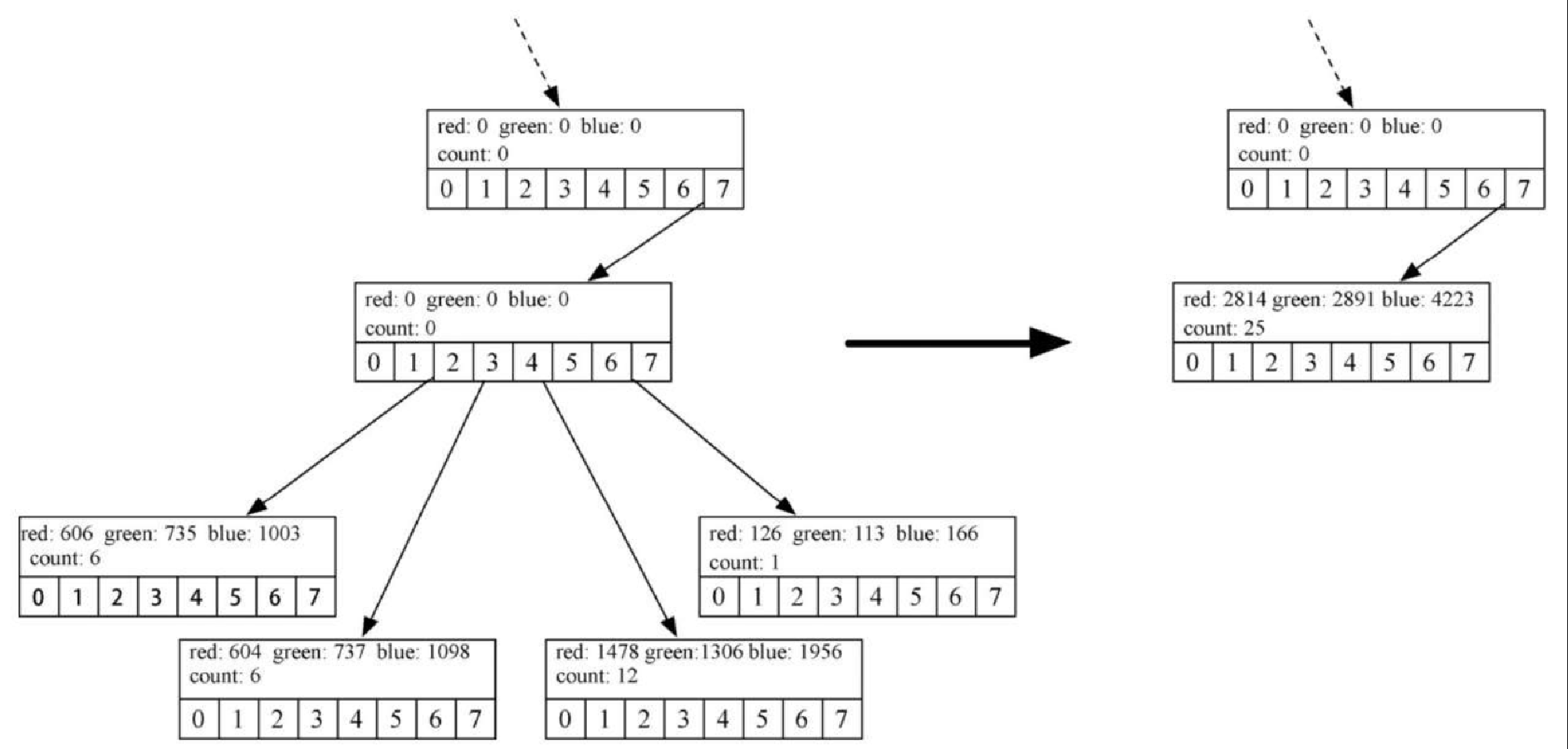
图8-19 给出了 4 个叶子节点的红、绿、蓝成分，分别是 (101, 122, 167)、(100,122, 183)、(123, 108, 163) 和 (126, 113, 166)。记住，这些值不同于图中标出的计数。注意，这 4 个叶子节点在颜色立方体中离得很近。由它们得到的新叶子节点的 id 是 (112, 115, 168)。这个值接近于 4 个值的均值，但更倾向于第 3 个颜色元组，因为第 3 个的引用计数是 12。

代码清单8-27 merge方法

def merge(self):
    for i in self.children:
        if i:
            if i.count > 0:
                self.oTree.leafList.remove(i)
                self.oTree.numLeaves -= 1
            else:
                print("Recursively Merging non-leaf ...")
                i.merge()
            self.count += i.count
            self.red += i.red
            self.green += i.green
            self.blue += i.blue

    for i in range(8):
        self.children[i] = None

因为 OctTree 只使用呈现在图片中的颜色，并且忠实地保留了常用的颜色，所以量化后的图片在质量上要比本节开头的简单方法得到的图片高得多。图8-20 是原始图片和量化图片的对比。

Figure 7. 图8-20 比较原始图片和利用OctTree量化的图片

还有很多其他的图片压缩算法，比如游程编码、离散余弦变换、霍夫曼编码等。理解这些算法并不难，希望你能查找相关资料并了解它们。另外，可以通过抖动这一技巧完善量化图片。抖动是指将不同的颜色靠近，让眼睛混合这些颜色，形成一张更真实的图片。这是报纸惯用的老把戏，通过黑色加上另 3 种颜色实现彩色印刷。你可以自行研究抖动的原理，并使它为你所用。