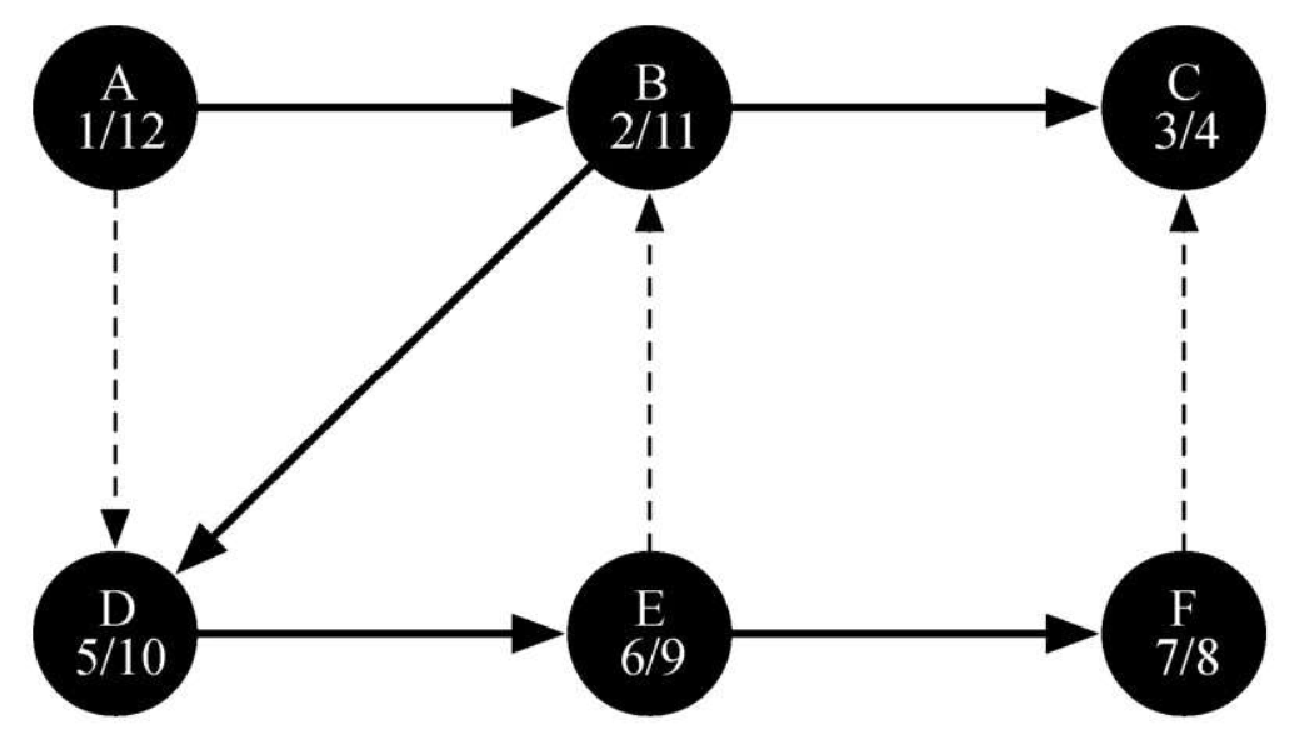
深度优先搜索
骑士周游问题
另一个经典问题是骑士周游问题,我们用它来说明第 2 种常见的图算法。为了解决骑士周游问题,我们取一块国际象棋棋盘和一颗骑士棋子(马)。目标是找到一系列走法,使得骑士对棋盘上的每一格刚好都只访问一次。这样的一个移动序列被称为 “周游路径”。多年来,骑士周游问题吸引了众多棋手、数学家和计算机科学家。对于 8×8 的棋盘,周游数的上界是 1.305×1035,但死路更多。很明显,解决这个问题需要聪明人或者强大的计算能力,抑或兼具二者。
尽管人们研究出很多种算法来解决骑士周游问题,但是图搜索算法是其中最好理解和最易编程的一种。我们再一次通过两步来解决这个问题:
-
用图表示骑士在棋盘上的合理走法;
-
使用图算法找到一条长度为 rows × columns-1 的路径,满足图中的每一个顶点都只被访问一次。
构建骑士周游图
为了用图表示骑士周游问题,我们将棋盘上的每一格表示为一个顶点,同时将骑士的每一次合理走法表示为一条边。图7-10 展示了骑士的合理走法以及在图中对应的边。
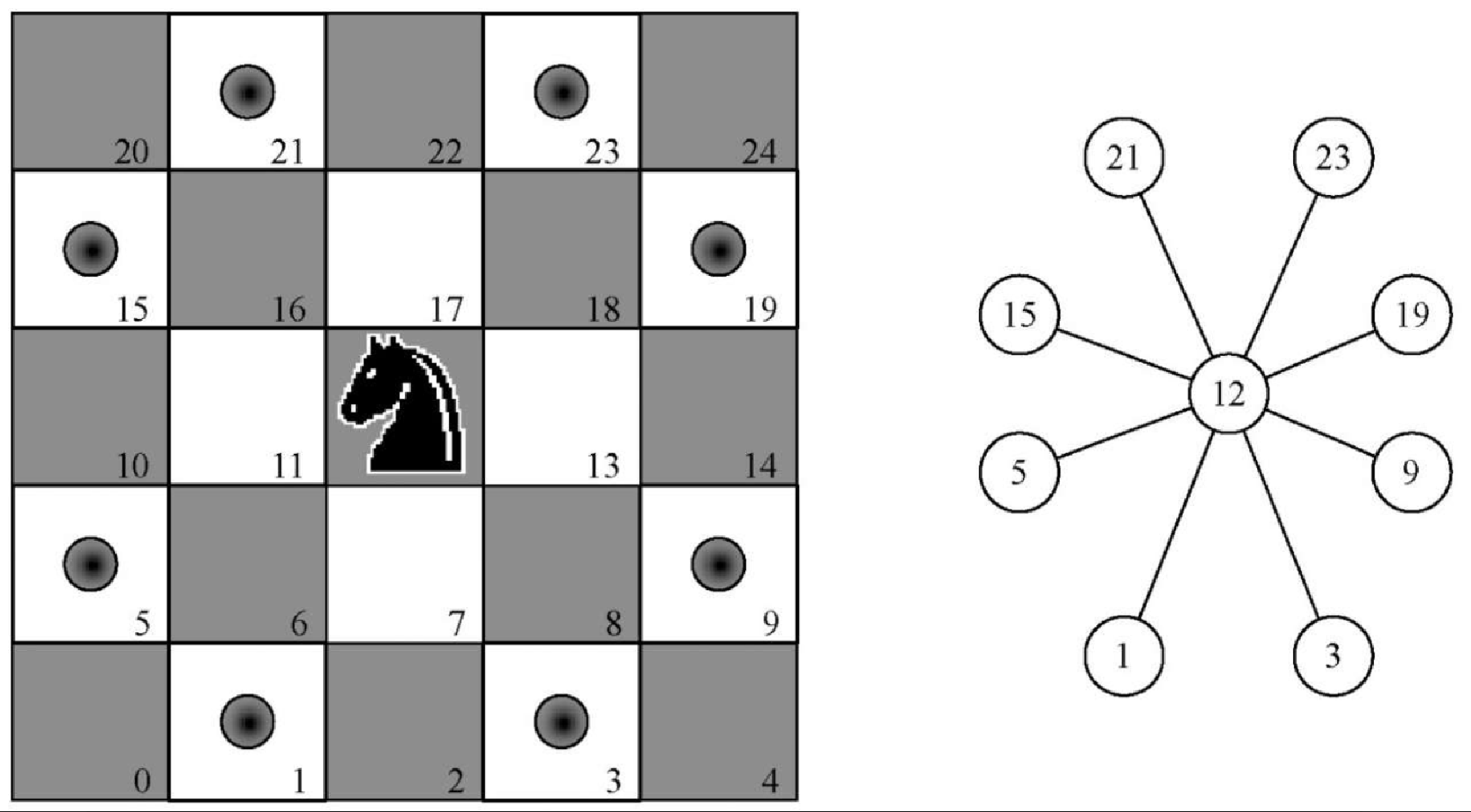
可以用代码清单 7-6 中的 Python 函数来构建 n × n 棋盘对应的完整图。knightGraph 函数将整个棋盘遍历了一遍。当它访问棋盘上的每一格时,都会调用辅助函数 genLegalMoves 来创建一个列表,用于记录从这一格开始的所有合理走法。之后,所有的合理走法都被转换成图中的边。另一个辅助函数 posToNodeId 将棋盘上的行列位置转换成与图 7-10 中顶点编号相似的线性顶点数。
from pythonds.graphs import Graph
def knightGraph(bdSize):
ktGraph = Graph()
for row in range(bdSize):
for col in range(bdSize):
nodeId = posToNodeId(row,col,bdSize)
newPositions = genLegalMoves(row,col,bdSize)
for e in newPositions:
nid = posToNodeId(e[0],e[1],bdSize)
ktGraph.addEdge(nodeId,nid)
return ktGraph
def posToNodeId(row, column, board_size):
return (row * board_size) + column在代码清单7-7 中,genLegalMoves 函数接受骑士在棋盘上的位置,并且生成 8 种可能的走法。legalCoord 辅助函数确认走法是合理的。
def genLegalMoves(x,y,bdSize):
newMoves = []
moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
if legalCoord(newX,bdSize) and \
legalCoord(newY,bdSize):
newMoves.append((newX,newY))
return newMoves
def legalCoord(x,bdSize):
if x >= 0 and x < bdSize:
return True
else:
return False图7-11展示了在 8×8 的棋盘上所有合理走法所对应的完整图,其中一共有 336 条边。注意,与棋盘中间的顶点相比,边缘顶点的连接更少。可以看到,这个图也是非常稀疏的。如果图是完全相连的,那么会有 4096 条边。由于本图只有 336条边,因此邻接矩阵的填充率只有 8.2%。
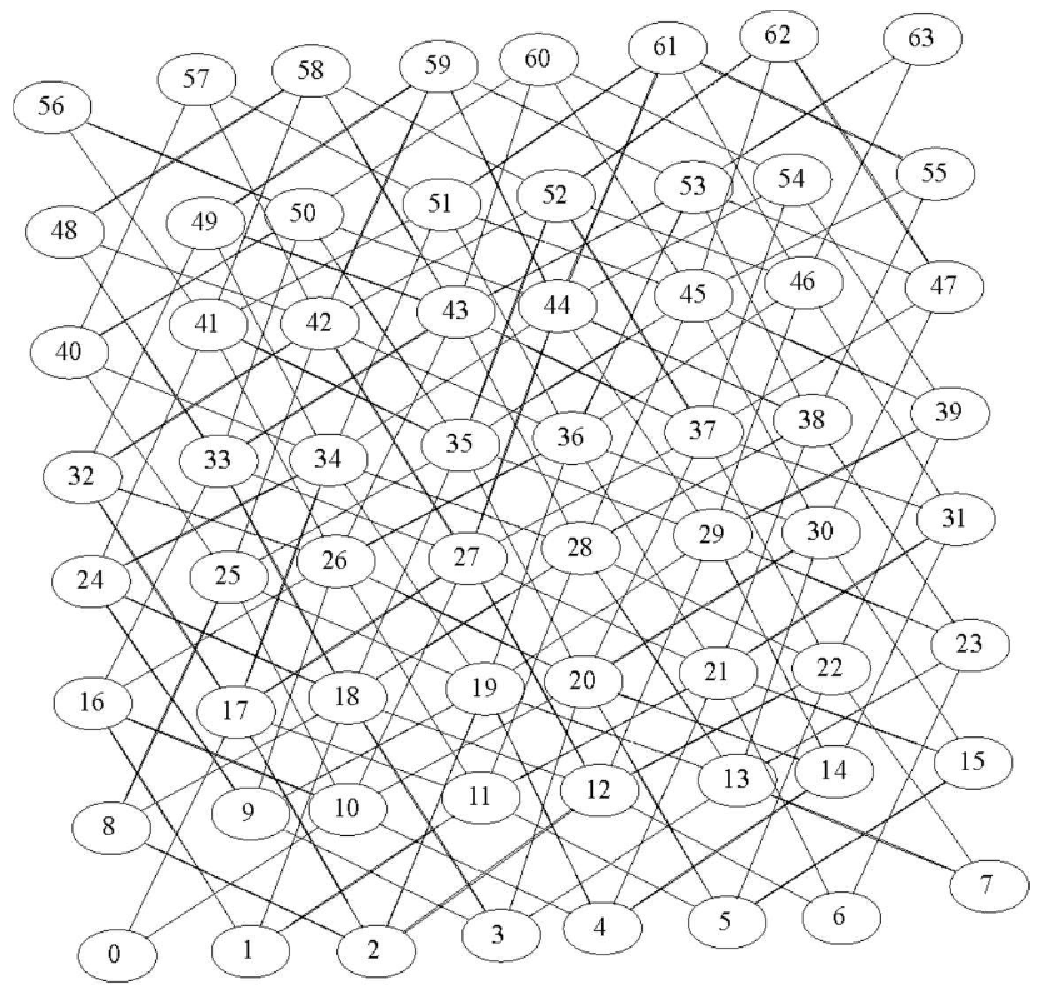
实现骑士周游
用来解决骑士周游问题的搜索算法叫作深度优先搜索(depth first search,以下简称 DFS)。与 BFS 每次构建一层不同,DFS 通过尽可能深地探索分支来构建搜索树。本节将探讨 DFS 的 2 种实现:第 1 种通过显式地禁止顶点被多次访问来直接解决骑士周游问题;第 2 种更通用,它在构建搜索树时允许其中的顶点被多次访问。本章稍后将利用第 2 种实现开发其他的图算法。
DFS 正是为找到由 63 条边构成的路径所需的算法。我们会看到,当 DFS 遇到死路时(无法找到下一个合理走法),它会回退到树中倒数第 2 深的顶点,以继续移动。
在代码清单 7-8 中,knightTour 函数接受 4 个参数:n 是搜索树的当前深度;path 是到当前为止访问过的顶点列表;u 是希望在图中访问的顶点;limit 是路径上的顶点总数。knightTour 函数是递归的。当被调用时,它首先检查基本情况。如果有一条包含 64 个顶点的路径,就从 knightTour 返回 True,以表示找到了一次成功的周游。如果路径不够长,则通过选择一个新的访问顶点并对其递归调用 knightTour 来进行更深一层的探索。
DFS 也使用颜色来记录已被访问的顶点。未访问的顶点是白色的,已被访问的则是灰色的。如果一个顶点的所有相邻顶点都已被访问过,但是路径长度仍然没有达到 64,就说明遇到了死路。如果遇到死路,就必须回溯。当从 knightTour 返回 False 时,就会发生回溯。在宽度优先搜索中,我们使用了队列来记录将要访问的顶点。由于深度优先搜索是递归的,因此我们隐式地使用一个栈来回溯。当从 knightTour 调用返回 False 时,仍然在 while 循环中,并且会查看 nbrList 中的下一个顶点。
代码清单7-8 knightTour 函数
from pythonds.graphs import Graph, Vertex
def knightTour(n,path,u,limit):
u.setColor('gray')
path.append(u)
if n < limit:
nbrList = list(u.getConnections())
i = 0
done = False
while i < len(nbrList) and not done:
if nbrList[i].getColor() == 'white':
done = knightTour(n+1, path, nbrList[i], limit)
i = i + 1
if not done: # prepare to backtrack
path.pop()
u.setColor('white')
else:
done = True
return done让我们通过一个例子来看看 knightTour 的运行情况,可以参照图7-12 来追踪搜索的变化。这个例子假设在代码清单7-8 中第 6 行对 getConnections 方法的调用将顶点按照字母顺序排好。首先调用 knightTour(0, path, A, 6)。
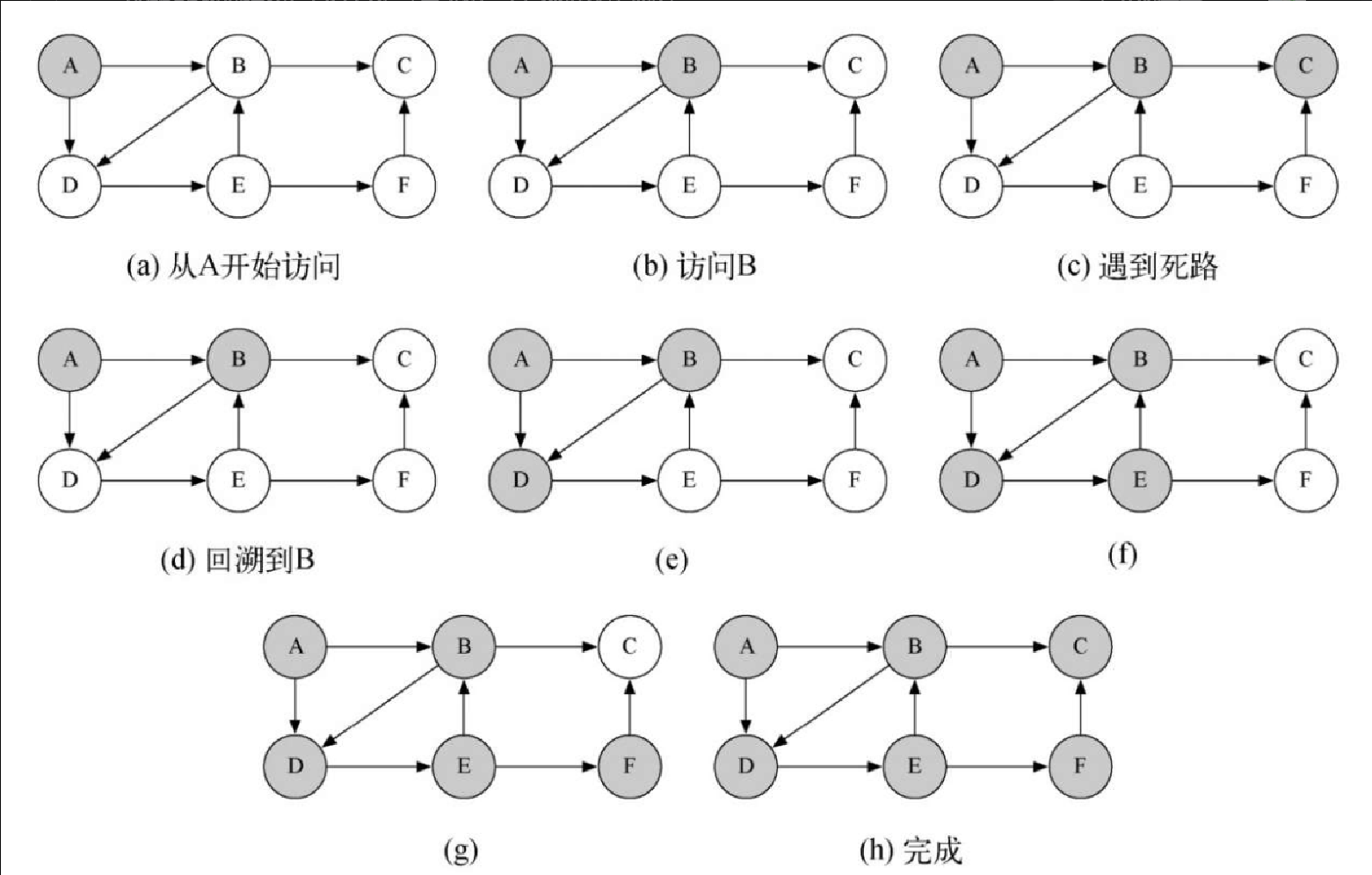
knightTour 函数从顶点 A 开始访问。与 A 相邻的顶点是 B 和 D。按照字母顺序,B 在 D 之前,因此 DFS 选择 B 作为下一个要访问的顶点,如图7-12b 所示。对 B 的访问从递归调用 knightTour 开始。B 与 C 和 D 相邻,因此 knightTour 接下来会访问 C。但是,C 没有白色的相邻顶点(如图7-12c 所示),因此是死路。此时,将 C 的颜色改回白色。knightTour 的调用返回 False,也就是将搜索回溯到顶点 B,如图7-12d所示。接下来要访问的顶点是 D,因此 knightTour 进行了一次递归调用来访问它。从顶点 D 开始,knightTour 可以继续进行递归调用,直到再一次访问顶点 C。但是,这一次,检验条件 n < limit 失败了,因此我们知道遍历完了图中所有的顶点。此时返回 True,以表明对图进行了一次成功的遍历。当返回列表时,path 包含 [A, B, D,E, F, C]。其中的顺序就是每个顶点只访问一次所需的顺序。
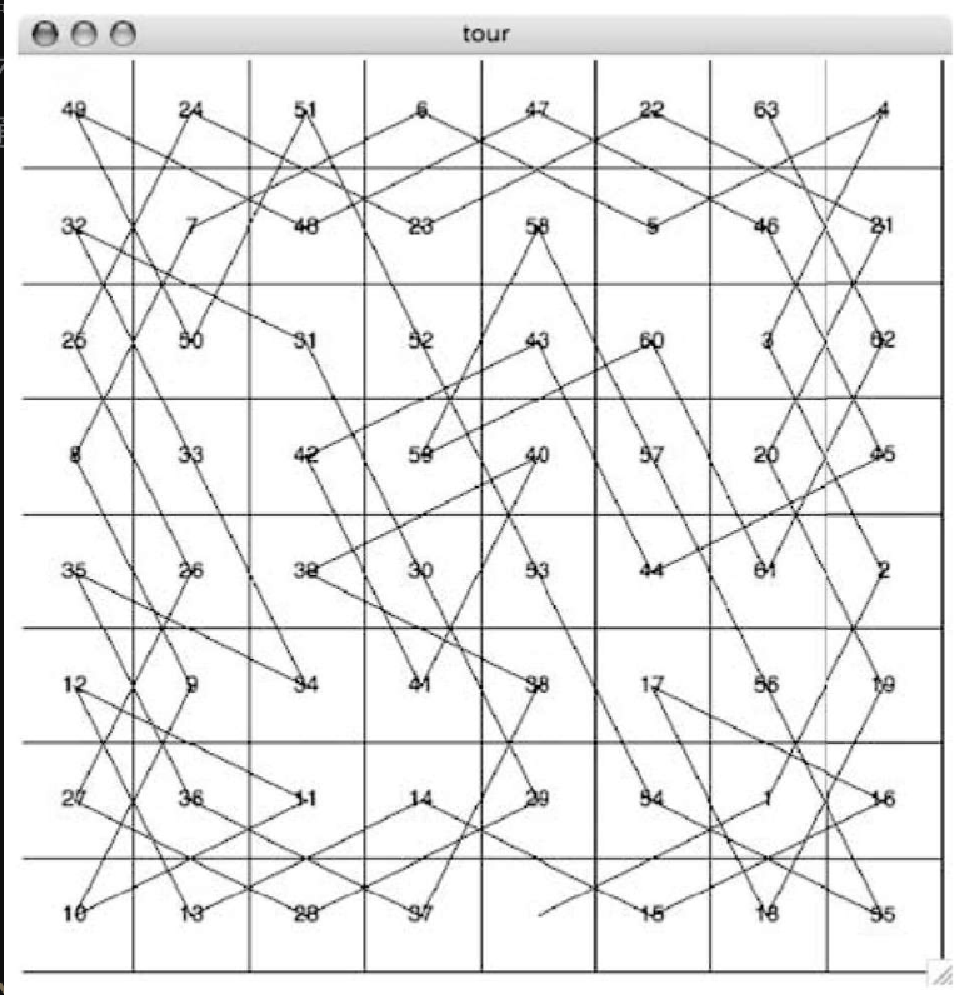
图7-13展示了在 8×8 的棋盘上周游的完整路径。存在多条周游路径,其中有一些是对称的。通过一些修改之后,可以实现循环周游,即起点和终点在同一个位置。
分析骑士周游
在学习深度优先搜索的通用版本之前,我们探索骑士周游问题中的最后一个有趣的话题:性能。具体地说,knightTour 对用于选择下一个访问顶点的方法非常敏感。例如,利用速度正常的计算机,可以在 1.5 秒之内针对 5×5 的棋盘生成一条周游路径。但是,如果针对 8×8 的棋盘,会怎么样呢?可能需要等待半个小时才能得到结果!
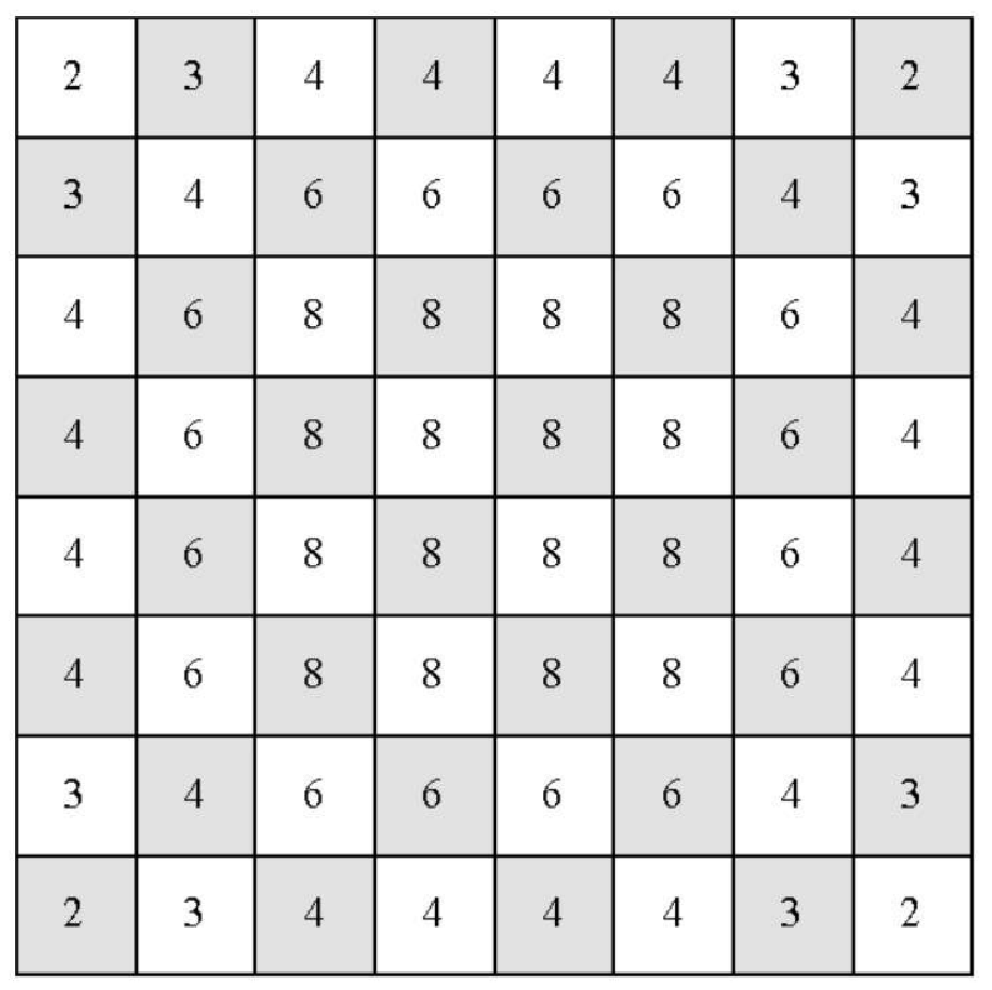
如此耗时的原因在于,目前实现的骑士周游问题算法是一种 \$O(k^N)\$的指数阶算法,其中 N 是棋盘上的格子数,k是一个较小的常量。图7-14 有助于理解搜索过程。树的根节点代表搜索过程的起点。从起点开始,算法生成并且检测骑士能走的每一步。如前所述,合理走法的数目取决于骑士在棋盘上的位置。若骑士位于四角,只有 2 种合理走法;若位于与四角相邻的格子中,则有 3 种合理走法;若在棋盘中央,则有 8 种合理走法。图7-15 展示了棋盘上的每一格所对应的合理走法数目。在树的下一层,对于骑士当前位置来说,又有 2~8 种不同的合理走法。待检查位置的数目对应搜索树中的节点数目。
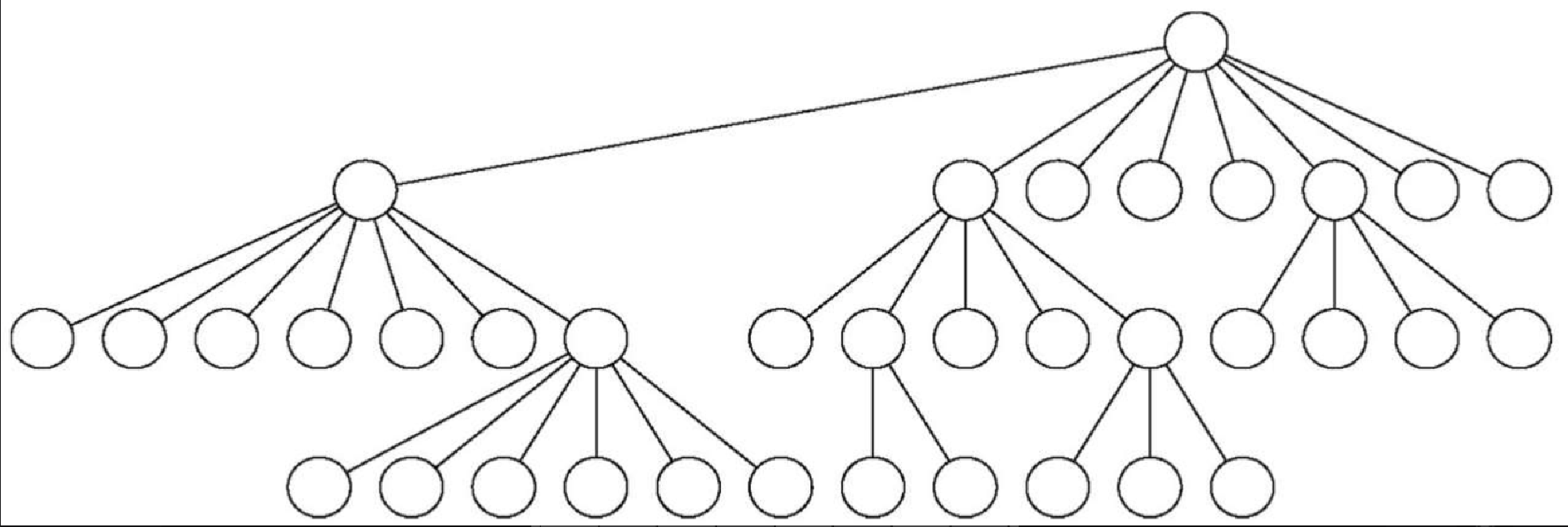
我们已经看到,在高度为 N 的二叉树中,节点数为 2N+1-1;至于子节点可能多达 8 个而非 2 个的树,其节点数会更多。由于每一个节点的分支数是可变的,因此可以使用平均分支因子来估计节点数。需要注意的是,这个算法是指数阶算法:kN+1-1,其中 k 是棋盘的平均分支因子。让我们看看它增长得有多快。对于 5×5 的棋盘,搜索树有 25 层(若把顶层记为第 0 层,则 N = 24),平均分支因子 k = 3.8。因此,搜索树中的节点数是 3.825-1 或者 3.12×1014。对于 6×6 的棋盘,k = 4.4,搜索树有 1.5×1023 个节点。对于 8×8 的棋盘,k = 5.25,搜索树有 1.3×1046 个节点。由于这个问题有很多个解,因此不需要访问搜索树中的每一个节点。但是,需要访问的节点的小数部分只是一个常量乘数,它并不能改变该问题的指数特性。我们把将k表达成棋盘大小的函数留作练习。
幸运的是,有办法针对 8×8 的棋盘在 1 秒内得到一条周游路径。代码清单 7-9 展示了加速搜索过程的代码。orderByAvail 函数用于替换代码清单 7-8 中第 6 行的 u.getConnections 调用。在 orderByAvail 函数中,第 10 行是最重要的一行。这一行保证接下来要访问的顶点有最少的合理走法。你可能认为这样做非常影响性能;为什么不选择合理走法最多的顶点呢?运行该程序,并在排序语句之后插入 resList.reverse(),便可轻松找到原因。
def orderByAvail(n):
resList = []
for v in n.getConnections():
if v.getColor() == 'white':
c = 0
for w in v.getConnections():
if w.getColor() == 'white':
c = c + 1
resList.append((c,v))
resList.sort(key=lambda x: x[0])
return [y[1] for y in resList]选择合理走法最多的顶点作为下一个访问顶点的问题在于,它会使骑士在周游的前期就访问位于棋盘中间的格子。当这种情况发生时,骑士很容易被困在棋盘的一边,而无法到达另一边的那些没访问过的格子。首先访问合理走法最少的顶点,则可使骑士优先访问棋盘边缘的格子。这样做保证了骑士能够尽早访问难以到达的角落,并且在需要的时候通过中间的格子跨越到棋盘的另一边。我们称利用这类知识来加速算法为启发式技术。人类每天都在使用启发式技术做决定,启发式搜索也经常被用于人工智能领域。本例用到的启发式技术被称作 Warnsdorff 算法,以纪念在 1823 年提出该算法的数学家 H. C. Warnsdorff。
通用深度优先搜索
骑士周游是深度优先搜索的一种特殊情况,它需要创建没有分支的最深深度优先搜索树。通用的深度优先搜索其实更简单,它的目标是尽可能深地搜索,尽可能多地连接图中的顶点,并且在需要的时候进行分支。
一次深度优先搜索甚至能够创建多棵深度优先搜索树,我们称之为深度优先森林。和宽度优先搜索类似,深度优先搜索也利用前驱连接来构建树。此外,深度优先搜索还会使用 Vertex 类中的两个额外的实例变量:发现时间记录算法在第一次访问顶点时的步数,结束时间记录算法在顶点被标记为黑色时的步数。在学习之后会发现,顶点的发现时间和结束时间提供了一些有趣的特性,后续算法会用到这些特性。
深度优先搜索的实现如代码清单 7-10 所示。由于 dfs 函数和 dfsvisit 辅助函数使用一个变量来记录调用 dfsvisit 的时间,因此我们选择将代码作为 Graph 类的一个子类中的方法来实现。该实现继承 Graph 类,并且增加了 time 实例变量,以及 dfs 和 dfsvisit 两个方法。注意第 11 行,dfs 方法遍历图中所有的顶点,并对白色顶点调用 dfsvisit 方法。之所以遍历所有的顶点,而不是简单地从一个指定的顶点开始搜索,是因为这样做能够确保深度优先森林中的所有顶点都在考虑范围内,而不会有被遗漏的顶点。for aVertex in self 这条语句可能看上去不太正确,但是此处的 self 是 DFSGraph 类的一个实例,遍历一个图实例中的所有顶点其实是一件非常自然的事情。
from pythonds.graphs import Graph
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred(-1)
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)尽管本例中的 bfs 实现只对回到起点的路径上的顶点感兴趣,但也可以创建一个表示图中所有顶点间的最短路径的宽度优先森林。这个问题留作练习。在接下来的两个例子中,我们会看到为何记录深度优先森林十分重要。
从 startVertex 开始,dfsvisit 方法尽可能深地探索所有相邻的白色顶点。如果仔细观察dfsvisit 的代码并且将其与 bfs 比较,应该注意到二者几乎一样,除了内部 for 循环的最后一行,dfsvisit 通过递归地调用自己来继续进行下一层的搜索,bfs 则将顶点添加到队列中,以供后续搜索。有趣的是,bfs 使用队列,dfsvisit 则使用栈。我们没有在代码中看到栈,但是它其实隐式地存在于 dfsvisit 的递归调用中。
图7-16 展示了在小型图上应用深度优先搜索算法的过程。图中,虚线表示被检查过的边,但是其一端的顶点已经被添加到深度优先搜索树中。在代码中,这是通过检查另一端的顶点是否不为白色来完成的。
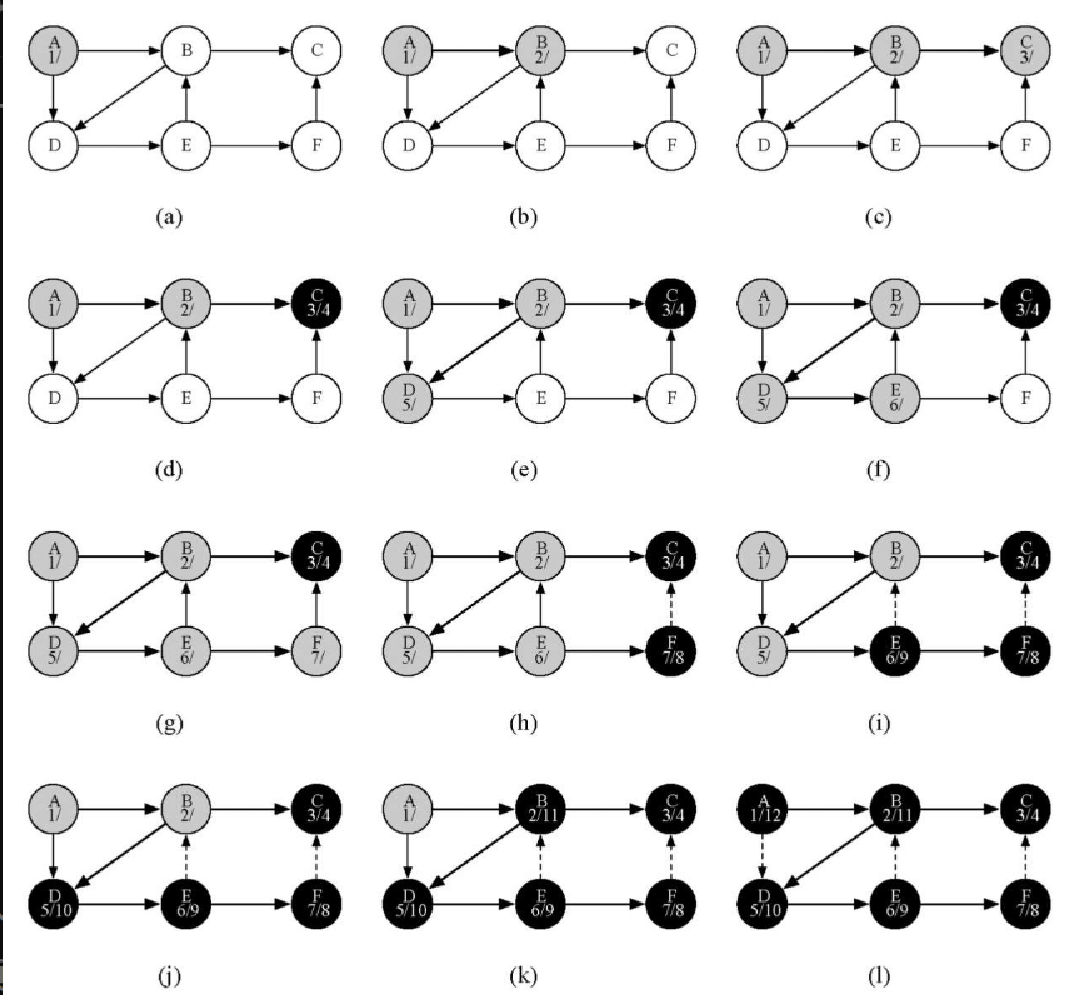
搜索从图中的顶点 A 开始。由于所有顶点一开始都是白色的,因此算法会访问 A。访问顶点的第一步是将其颜色设置为灰色,以表明正在访问该顶点,并将其发现时间设为 1。由于 A 有两个相邻顶点(B 和 D),因此它们都需要被访问。我们按照字母顺序来访问顶点。
接下来访问顶点 B,将它的颜色设置为灰色,并把发现时间设置为 2。B 也与两个顶点(C 和 D)相邻,因此根据字母顺序访问 C。
访问 C 时,搜索到达某个分支的终点。在将 C 标为灰色并且把发现时间设置为 3 之后,算法发现 C 没有相邻顶点。这意味着对 C 的探索完成,因此将它标为黑色,并将完成时间设置为 4。图7-16d 展示了搜索至这一步时的状态。
由于 C 是一个分支的终点,因此需要返回到 B,并且继续探索其余的相邻顶点。唯一的待探索顶点就是 D,它把搜索引到 E。E 有两个相邻顶点,即 B 和 F。正常情况下,应该按照字母顺序来访问这两个顶点,但是由于 B 已经被标记为灰色,因此算法自知不应该访问 B,因为如果这么做就会陷入死循环。因此,探索过程跳过 B,继续访问 F。
F 只有 C 这一个相邻顶点,但是 C 已经被标记为黑色,因此没有后续顶点需要探索,也即到达另一个分支的终点。从此时起,算法一路回溯到起点,同时为各个顶点设置完成时间并将它们标记为黑色,如图7-16h~图7-16l所示。
每个顶点的发现时间和结束时间都体现了括号特性,这意味着深度优先搜索树中的任一节点的子节点都有比该节点更晚的发现时间和更早的结束时间。图7-17 展示了通过深度优先搜索算法构建的树。