递归可视化

前文探讨了一些能用递归轻松解决的问题。但是，要想象递归的样子或者将递归过程可视化仍然十分困难。这使得递归难以掌握。本节将探讨一系列使用递归来绘制有趣图案的例子。看着这些图案一点一点地形成，你会对递归过程有新的认识，从而深刻地理解递归的概念。

我们将使用 Python 的 turtle 模块来绘制图案。Python 的各个版本都提供 turtle 模块，它用起来非常简便。顾名思义，可以用 turtle 模块创建一只小乌龟（turtle）并让它向前或向后移动，或者左转、右转。小乌龟的尾巴可以抬起或放下。当尾巴放下时，移动的小乌龟会在其身后画出一条线。若要增加美观度，可以改变小乌龟尾巴的宽度以及尾尖所蘸墨水的颜色。

让我们通过一个简单的例子来展示小乌龟绘图的过程。使用 turtle 模块递归地绘制螺旋线，如代码清单4-5 所示。先导入 turtle 模块，然后创建一个小乌龟对象，同时也会创建用于绘制图案的窗口。接下来定义 drawSpiral 函数。这个简单函数的基本情况是，要画的线的长度（参数 len）降为 0。如果线的长度大于 0，就让小乌龟向前移动 len 个单位距离，然后向右转 90 度。递归发生在用缩短后的距离再一次调用 drawSpiral 函数时。代码清单4-5 在结尾处调用了 myWin.exitonclick() 函数，这使小乌龟进入等待模式，直到用户在窗口内再次点击之后，程序清理并退出。

代码清单4-5 用turtle模块递归地绘制螺旋线

import turtle

myTurtle = turtle.Turtle()
myWin = turtle.Screen()

def drawSpiral(myTurtle, lineLen):
    if lineLen > 0:
        myTurtle.forward(lineLen)
        myTurtle.right(90)
        drawSpiral(myTurtle,lineLen-5)

drawSpiral(myTurtle,100)
myWin.exitonclick()

理解了这个例子的原理，便能用 turtle 模块绘制漂亮的图案。接下来绘制一棵分形树。分形是数学的一个分支，它与递归有很多共同点。分形的定义是，不论放大多少倍来观察分形图，它总是有相同的基本形状。自然界中的分形例子包括海岸线、雪花、山岭，甚至树木和灌木丛。众多自然现象中的分形本质使得程序员能够用计算机生成看似非常真实的电影画面。下面来生成一棵分形树。

思考如何用分形来描绘一棵树。如前所述，不论放大多少倍，分形图看起来都一样。对于树木来说，这意味着即使是一根小嫩枝也有和一整棵树一样的形状和特征。借助这一思想，可以把树定义为树干，其上长着一棵向左生长的子树和一棵向右生长的子树。因此，可以将树的递归定义运用到它的左右子树上。

让我们将上述想法转换成 Python 代码。代码清单4-6 展示了如何用 turtle 模块绘制分形树。仔细研究这段代码，会发现第 5 行和第 7 行进行了递归调用。第 5 行在小乌龟向右转了 20 度之后立刻进行递归调用，这就是之前提到的右子树。然后，第 7 行再一次进行递归调用，但这次是在向左转了 40 度以后。之所以需要让小乌龟左转 40 度，是因为它首先需要抵消之前右转的 20 度，然后再继续左转 20 度来绘制左子树。同时注意，每一次进行递归调用时，都从参数 branchLen 中减去一些，这是为了让递归树越来越小。第 2 行的 if 语句会检查 branchLen 是否满足基本情况。

代码清单4-6 绘制分形树

def tree(branchLen,t):
    if branchLen > 5:
        t.forward(branchLen)
        t.right(20)
        tree(branchLen-15,t)
        t.left(40)
        tree(branchLen-10,t)
        t.right(20)
        t.backward(branchLen)

请执行分形树的代码，但在此之前，先想象一下绘制出来的树会是什么样。这棵树是如何开枝散叶的呢？程序是会同时对称地绘制左右子树，还是会先绘制右子树再绘制左子树？在输入 tree 函数的代码之后，可以用下面的代码来绘制一棵树。

>>> from turtle import *
>>> t = Turtle()
>>> myWin = t.getscreen()
>>> t.left(90)
>>> t.up()
>>> t.backward(300)
>>> t.down()
>>> t.color('green')
>>> tree(110, t)
>>> myWin.exitonclick()

注意，树上的每一个分支点都对应一次递归调用，而且程序先绘制右子树，并一路到其最短的嫩枝，如图4-7 所示。接着，程序一路反向回到树干，以此绘制完右子树，如图4-8 所示。然后，开始绘制左子树，但并不是一直往左延伸到最左端的嫩枝。相反，左子树自己的右子树被完全画好后才会绘制最左端的嫩枝。

Figure 1. 图4-7 先绘制右子树

Figure 2. 图4-8 分形树的右半部分

这个简单的分形树程序仅仅是一个开始。你会注意到，绘制出来的树看上去并不真实，这是由于自然界并不如计算机程序一样对称。在本章最后的练习中，你将探索如何绘制出看起来更真实的树。

谢尔平斯基三角形

另一个具有自相似性的分形图是谢尔平斯基三角形，如图4-9 所示。谢尔平斯基三角形展示了三路递归算法。手动绘制谢尔平斯基三角形的过程十分简单：从一个大三角形开始，通过连接每条边的中点将它分割成四个新的三角形；忽略中间的三角形，利用同样的方法分割其余三个三角形。每一次创建一个新三角形集合，都递归地分割三个三角形。如果笔尖足够细，可以无限地重复这一分割过程。在继续阅读之前，不妨试着亲手绘制谢尔平斯基三角形。

Figure 3. 图4-9 谢尔平斯基三角形

既然可以无限地重复分割算法，那么它的基本情况是什么呢？答案是，基本情况根据我们想要的分割次数设定。这个次数有时被称为分形图的 “度”。每进行一次递归调用，就将度减 1，直到度是 0 为止。代码清单4-7 展示了生成如图4-9 所示的谢尔平斯基三角形的代码。

代码清单4-7 绘制谢尔平斯基三角形

import turtle

def drawTriangle(points,color,myTurtle):
    myTurtle.fillcolor(color)
    myTurtle.up()
    myTurtle.goto(points[0][0],points[0][1])
    myTurtle.down()
    myTurtle.begin_fill()
    myTurtle.goto(points[1][0],points[1][1])
    myTurtle.goto(points[2][0],points[2][1])
    myTurtle.goto(points[0][0],points[0][1])
    myTurtle.end_fill()

def getMid(p1,p2):
    return ( (p1[0]+p2[0]) / 2, (p1[1] + p2[1]) / 2)

def sierpinski(points,degree,myTurtle):
    colormap = ['blue','red','green','white','yellow',
                'violet','orange']
    drawTriangle(points,colormap[degree],myTurtle)
    if degree > 0:
        sierpinski([points[0],
                        getMid(points[0], points[1]),
                        getMid(points[0], points[2])],
                   degree-1, myTurtle)
        sierpinski([points[1],
                        getMid(points[0], points[1]),
                        getMid(points[1], points[2])],
                   degree-1, myTurtle)
        sierpinski([points[2],
                        getMid(points[2], points[1]),
                        getMid(points[0], points[2])],
                   degree-1, myTurtle)

def main():
   myTurtle = turtle.Turtle()
   myWin = turtle.Screen()
   myPoints = [[-100,-50],[0,100],[100,-50]]
   sierpinski(myPoints,3,myTurtle)
   myWin.exitonclick()

main()

代码清单4-7 中的程序遵循了之前描述的思想。sierpinski 首先绘制外部的三角形，接着进行 3 个递归调用，每一个调用对应生成的一个新三角形。本例再一次使用 Python 自带的标准 turtle 模块。在 Python 解释器中执行 help('turtle')，可以详细了解 turtle 模块中的所有方法。

请根据代码清单4-7 思考三角形的绘制顺序。假设三个角的顺序是左下角、顶角、右下角。由于 sierpinski 的递归调用方式，它会一直在左下角绘制三角形，直到绘制完最小的三角形才会往回绘制剩下的三角形。之后，它会开始绘制顶部的三角形，直到绘制完最小的三角形。最后，它会绘制右下角的三角形，直到全部绘制完成。

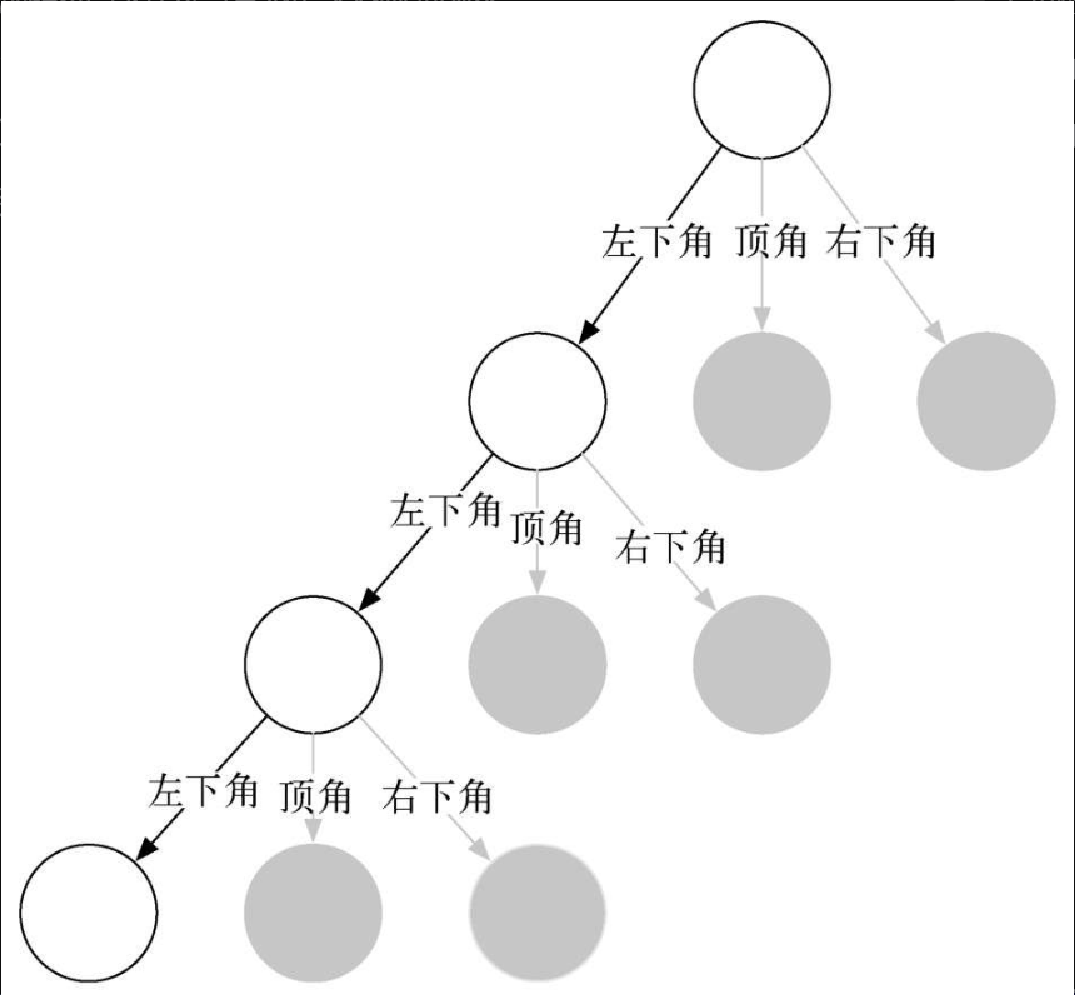
函数调用图有助于理解递归算法。由图4-10 可知，递归调用总是往左边进行的。在图中，黑线表示正在执行的函数，灰线表示没有被执行的函数。越深入到该图的底部，三角形就越小。函数一次完成一层的绘制；一旦它绘制好底层左边的三角形，就会接着绘制底层中间的三角形，依此类推。

Figure 4. 图4-10 谢尔平斯基三角形的函数调用图

sierpinski 函数非常依赖于 getMid 函数，后者接受两个点作为输入，并返回它们的中点。此外，代码清单4-7 中有一个函数使用 turtle 模块的 begin_fill 和 end_fill 绘制带颜色的三角形。这意味着谢尔平斯基三角形的每一层都有不同的颜色。