最短路径问题

当我们浏览网页、发送电子邮件，或者从校园的另一处登录实验室里的计算机时，在后台发生了很多事，信息从一台计算机传送到另一台计算机。深入地研究信息在多台计算机之间的传送过程，是计算机网络课程的主要内容。本节将适当地讨论互联网的运作机制，并以此介绍另一个非常重要的图算法。

图7-27 从整体上展示了互联网的通信机制。当我们使用浏览器访问某一台服务器上的网页时，访问请求必须通过路由器从本地局域网传送到互联网上，并最终到达该服务器所在局域网对应的路由器。然后，被请求的网页通过相同的路径被传送回浏览器。在图7-27 中，标有 “互联网” 的云图标中有众多额外的路由器，它们的工作就是协同将信息从一处传送到另一处。如果你的计算机支持 traceroute 命令，可以利用它亲眼看到许多路由器。图7-28 展示了 traceroute 命令的执行结果：在路德学院的 Web 服务器和明尼苏达大学的邮件服务器之间有 13 个路由器。

Figure 1. 图7-27 互联网通信概览

Figure 2. 图7-28 服务器之间的路由器

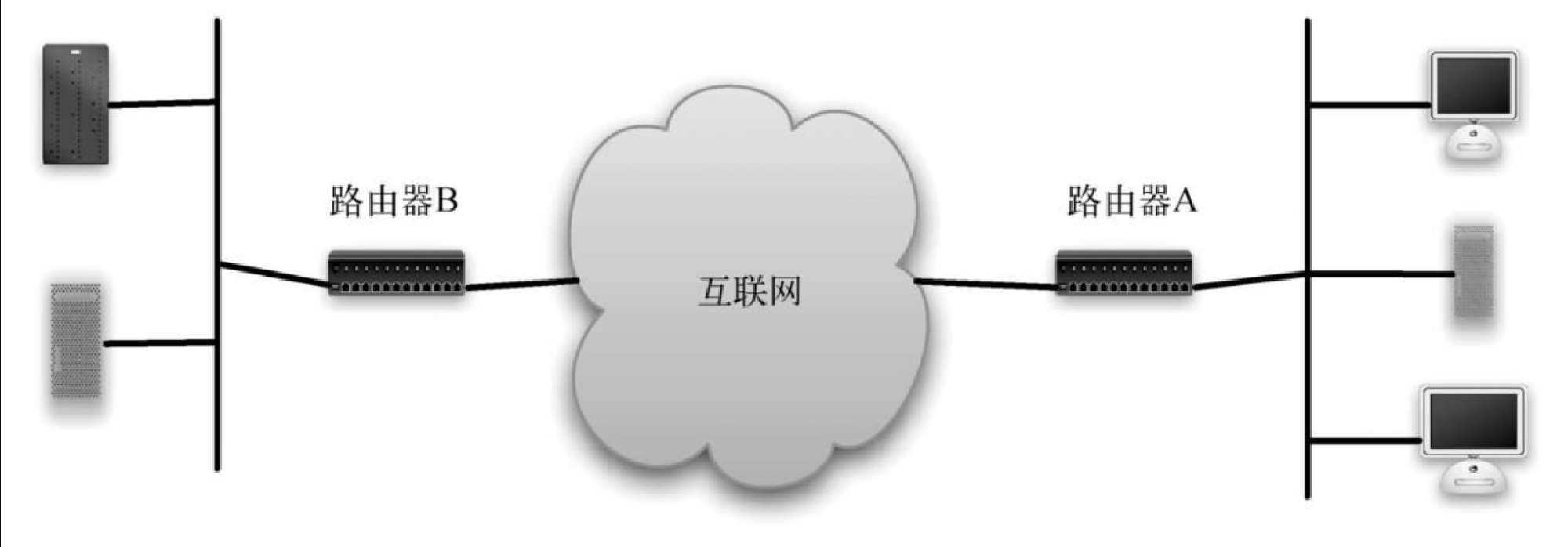
互联网上的每一个路由器都与一个或多个其他的路由器相连。如果在不同的时间执行 traceroute 命令，极有可能看到信息在不同的路由器间流动。这是由于一对路由器之间的连接存在着一定的成本，成本大小取决于流量、时间段以及众多其他因素。至此，你应该能够理解为何可以用带权重的图来表示路由器网络。

图7-29 展示了一个小型路由器网络对应的带权图。我们要解决的问题是为给定信息找到权重最小的路径。这个问题并不陌生，因为它和我们之前用宽度优先搜索解决过的问题十分相似，只不过现在考虑的是路径的总权重，而不是路径的长度。需要注意的是，如果所有的权重都相等，那么两个问题就没有区别。

Figure 3. 图7-29 小型路由器网络对应的带权图

Dijkstra算法

Dijkstra 算法可用于确定最短路径，它是一种循环算法，可以提供从一个顶点到其他所有顶点的最短路径。这与宽度优先搜索非常像。

为了记录从起点到各个终点的总开销，要利用 Vertex 类中的实例变量 dist。该实例变量记录从起点到当前顶点的最小权重路径的总权重。Dijkstra 算法针对图中的每个顶点都循环一次，但循环顺序是由一个优先级队列控制的。用来决定顺序的正是 dist。在创建顶点时，将 dist 设为一个非常大的值。理论上可以将 dist 设为无穷大，但是实际一般将其设为一个大于所有可能出现的实际距离的值。

Dijkstra 算法的实现如代码清单7-11 所示。当程序运行结束时，dist 和 predecessor 都会被设置成正确的值。

代码清单7-11 Dijkstra算法的Python实现

from pythonds.graphs import PriorityQueue, Graph, Vertex
def dijkstra(aGraph,start):
    pq = PriorityQueue()
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in aGraph])
    while not pq.isEmpty():
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
            newDist = currentVert.getDistance() \
                    + currentVert.getWeight(nextVert)
            if newDist < nextVert.getDistance():
                nextVert.setDistance( newDist )
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert,newDist)

Dijkstra 算法使用了优先级队列。你应该记得，第 6 章讲过如何用堆实现优先级队列。不过，第 6 章中的简单实现和用于 Dijkstra 算法的实现有几个不同点。首先，PriorityQueue 类存储了键-值对的二元组。这对于 Dijkstra 算法来说非常重要，因为优先级队列中的键必须与图中顶点的键相匹配。其次，二元组中的值被用来确定优先级，对应键在优先级队列中的位置。在 Dijkstra 算法的实现中，我们使用了顶点的距离作为优先级，这是因为我们总希望访问距离最小的顶点。另一个不同点是增加了 decreaseKey 方法（第 14 行）。当到一个顶点的距离减少并且该顶点已在优先级队列中时，就调用这个方法，从而将该顶点移向优先级队列的头部。

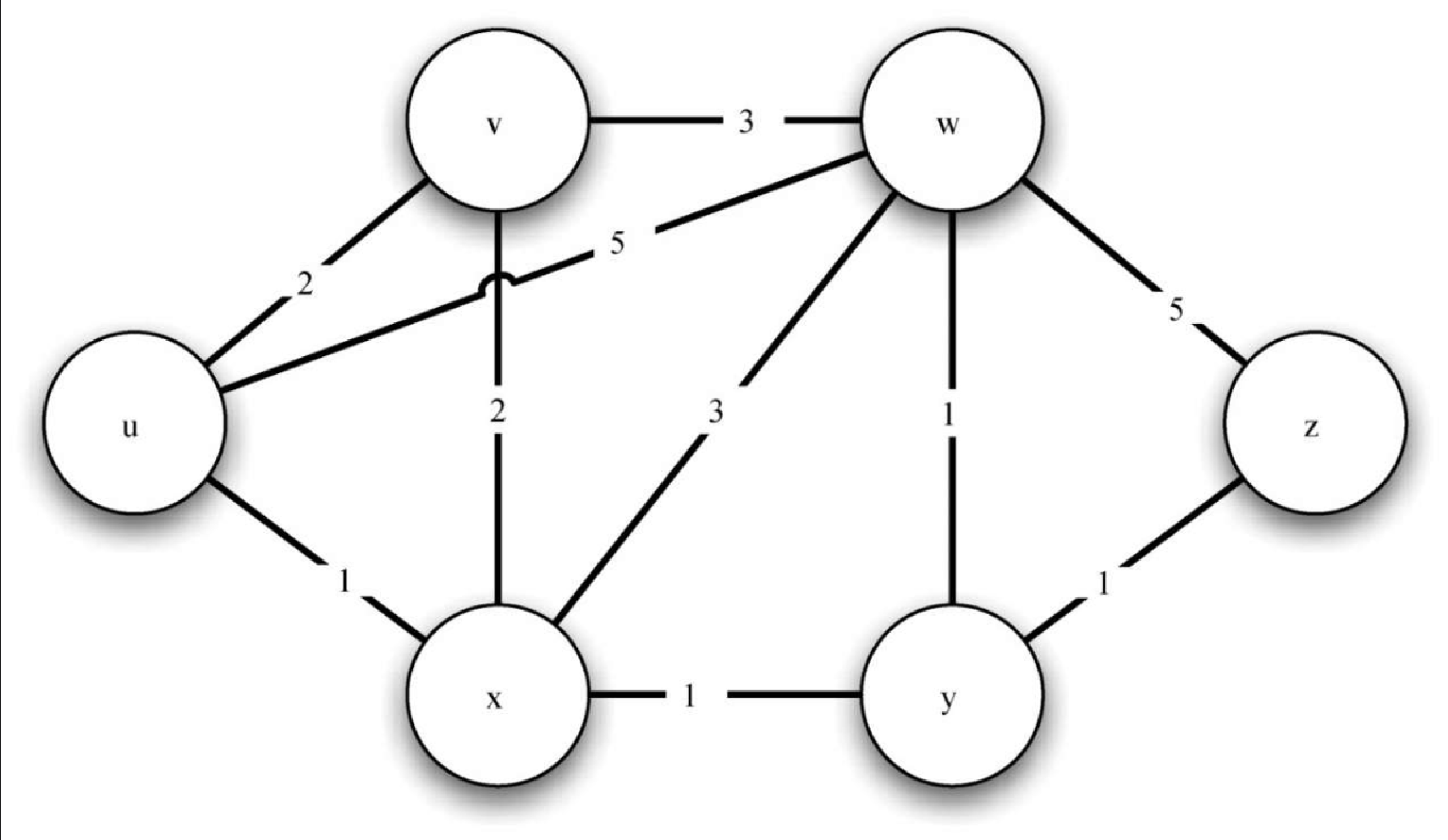
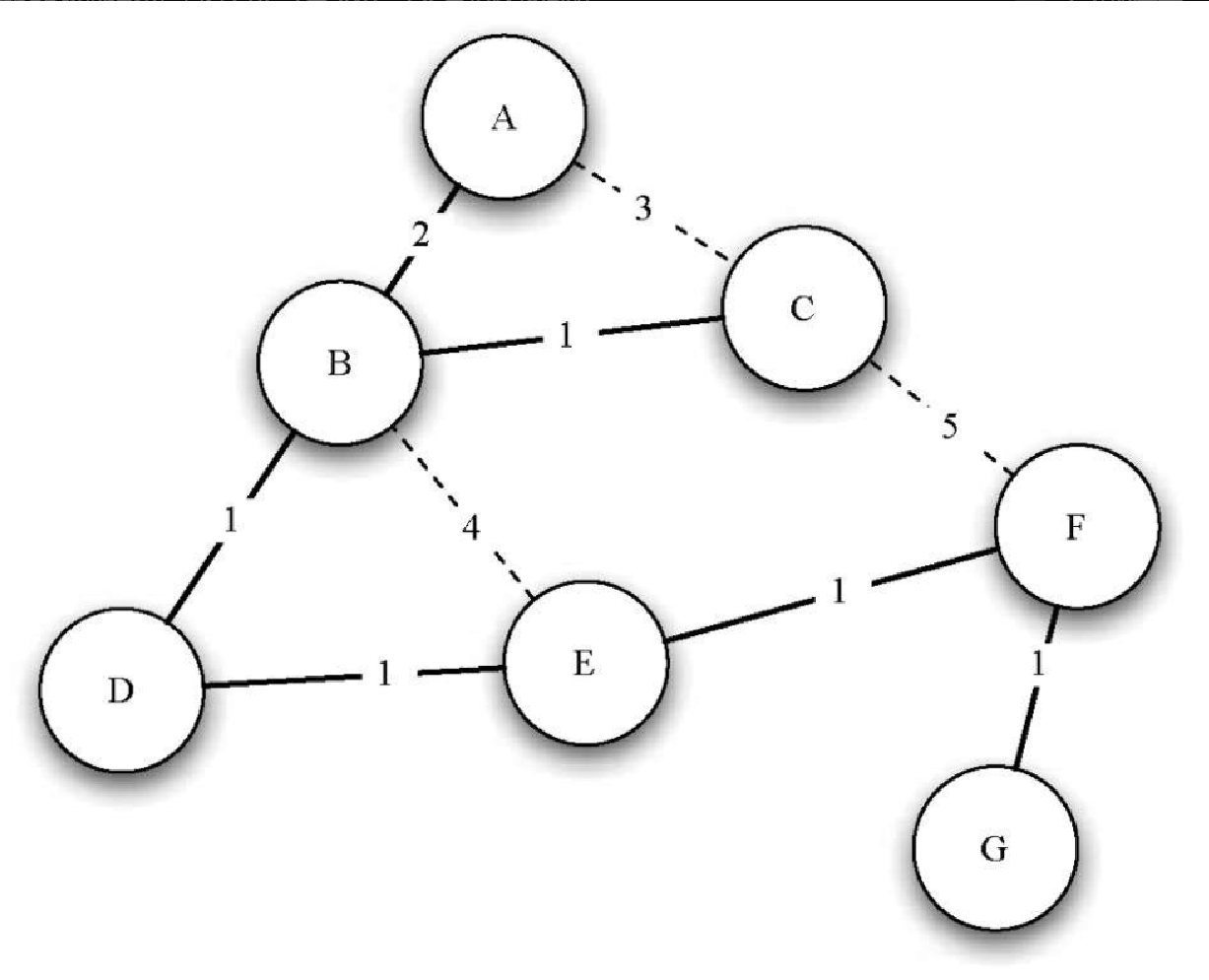
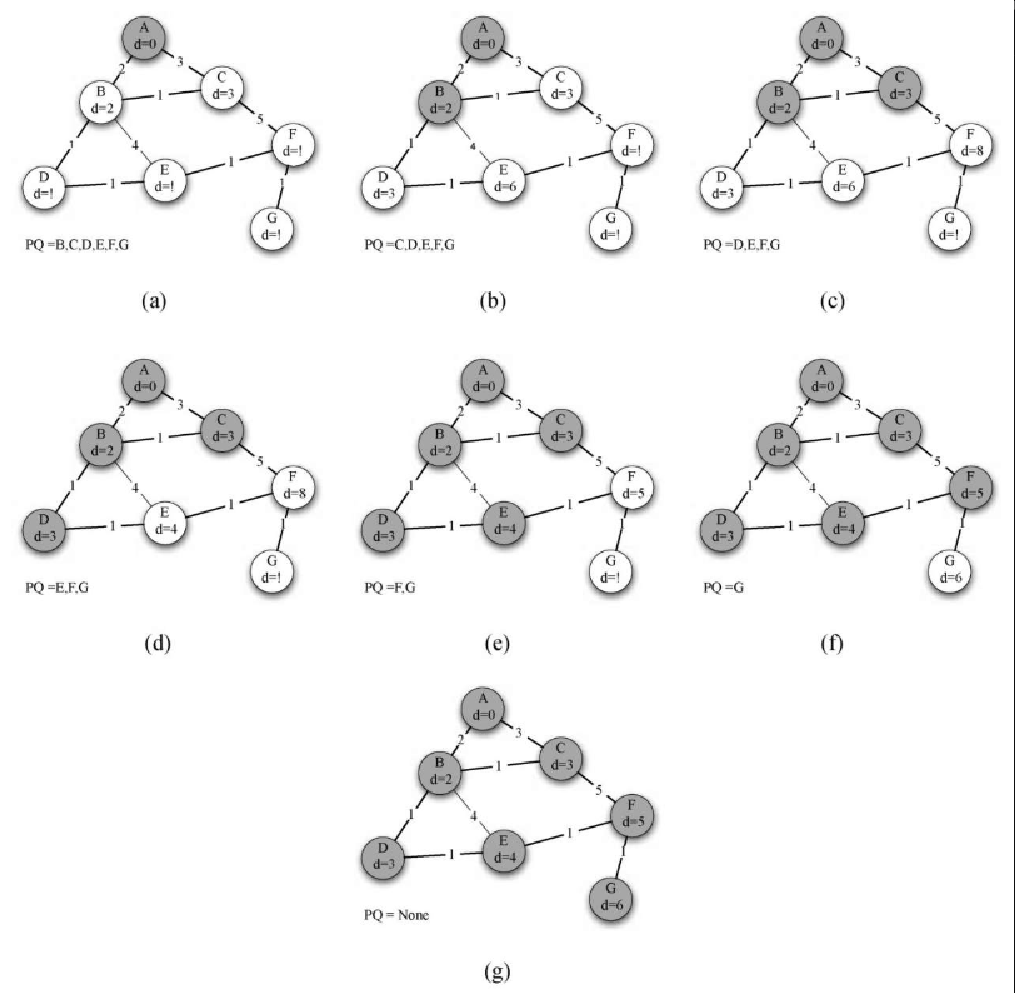
让我们对照图7-30 来理解如何针对每一个顶点应用 Dijkstra 算法。从顶点 u 开始，与 u 相邻的 3 个顶点分别是 v、w 和 x。由于到 v、w 和 x 的初始距离都是 sys.maxint，因此从起点到它们的新开销就是直接开销。更新这 3 个顶点的开销，同时将它们的前驱顶点设置成 u，并将它们添加到优先级队列中。我们使用距离作为优先级队列的键。此时，算法运行的状态如图7-30a 所示。

Figure 4. 图7-30 Dijkstra算法的应用过程

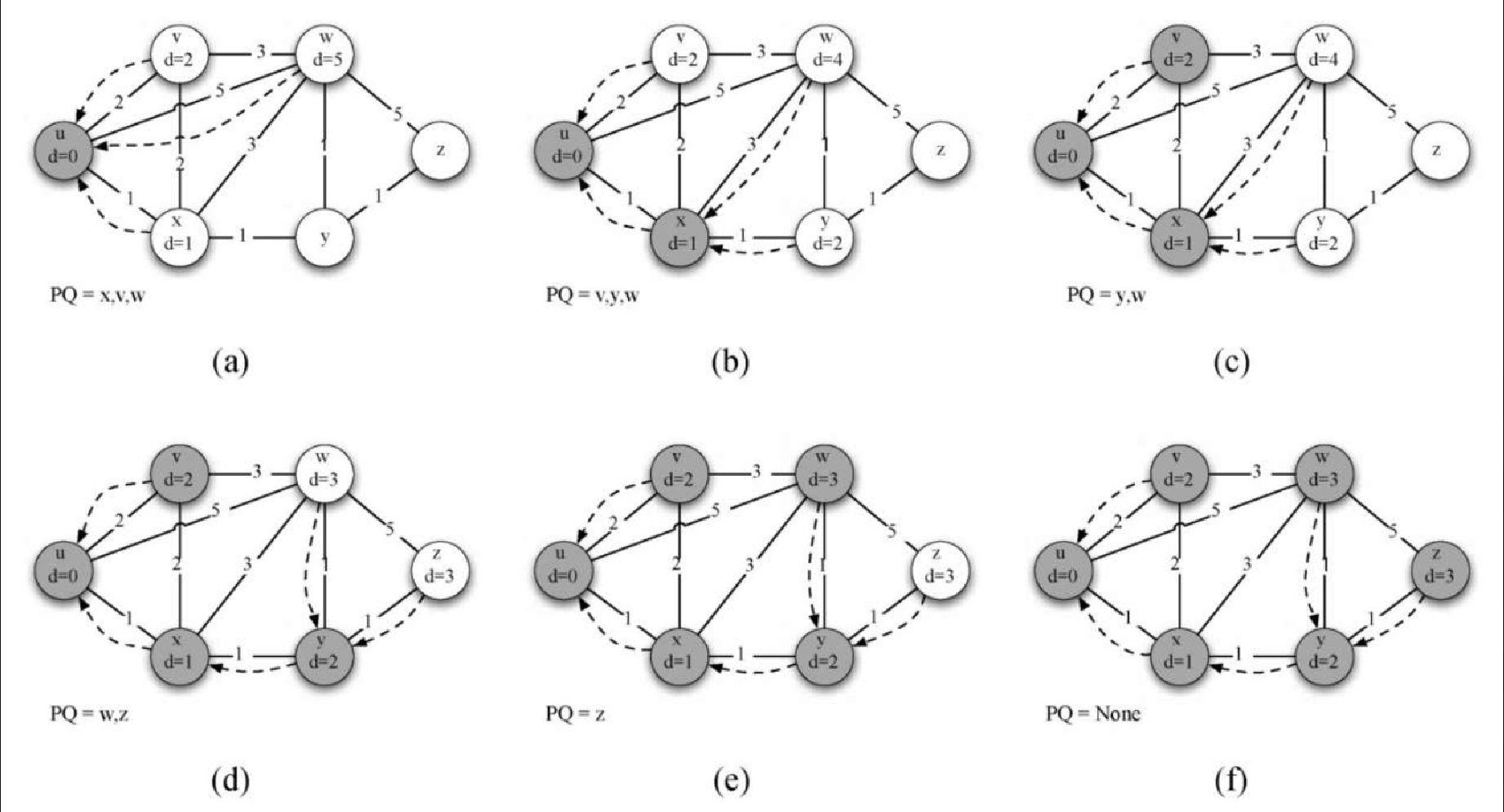
下一次 while 循环检查与x相邻的顶点。之所以 x 是第 2 个被访问的顶点，是因为它到起点的开销最小，因此排在了优先级队列的头部。与 x 相邻的有 u、v、w 和 y。对于每一个相邻顶点，检查经由 x 到它的距离是否比已知的距离更短。显然，对于 y 来说确实如此，因为它的初始距离是 sys.maxint；对于 u 和 v 来说则不然，因为它们的距离分别为 0 和 2。但是，我们发现经过 x 到 w 的距离比直接从 u 到 w 的距离要短。因此，将到达 w 的距离更新为更短的值，并且将 w 的前驱顶点从 u 改为 x。图7-30b 展示了此时的状态。

下一步检查与 v 相邻的顶点。这一步没有对图做任何改动，因此我们继续检查顶点 y。此时，我们发现经由 y 到达 w 和 z 的距离都更短，因此相应地调整它们的距离及前驱顶点。最后检查 w 和 z，发现不需要做任何改动。由于优先级队列为空，因此退出。

非常重要的一点是，Dijkstra 算法只适用于边的权重均为正的情况。如果图7-29 中有一条边的权重为负，那么 Dijkstra 算法永远不会退出。

除了 Dijkstra 算法，还有其他一些算法被用于寻找最短路径。Dijkstra 算法的问题是需要有完整的图，这意味着每一个路由器都要知道整个互联网的路由器连接情况，而事实并非如此。Dijkstra 算法的一些变体允许每个路由器在运行时才发现图，例如 “距离向量” 路由算法。

分析Dijkstra算法

最后，我们来分析 Dijkstra 算法的时间复杂度。开始时，要将图中的每一个顶点都添加到优先级队列中，这个操作的时间复杂度是 \$O(V)\$。优先级队列构建完成之后，while 循环针对每一个顶点都执行一次，这是由于一开始所有顶点都被添加到优先级队列中，并且只在循环时才被移除。在循环内部，每次对 delMin 的调用都是 \$O(logV)\$。综合起来考虑，循环和 delMin 调用的总时间复杂度是 \$O(VlogV)\$。for 循环对图中的每一条边都执行一次，并且循环内部的 decreaseKey 调用为 \$O(ElogV)\$。因此，总的时间复杂度为 \$O((V+E)logV)\$。

Prim算法

在学习最后一个图算法之前，先考虑网络游戏设计师和互联网广播服务提供商面临的问题。他们希望高效地把信息传递给所有人。这在网络游戏中非常重要，因为所有玩家都可以据此知道其他玩家的最近位置。互联网广播也需要做到这一点，以让所有听众都接收到所需数据。图7-31 展示了上述广播问题。

Figure 5. 图7-31 广播问题

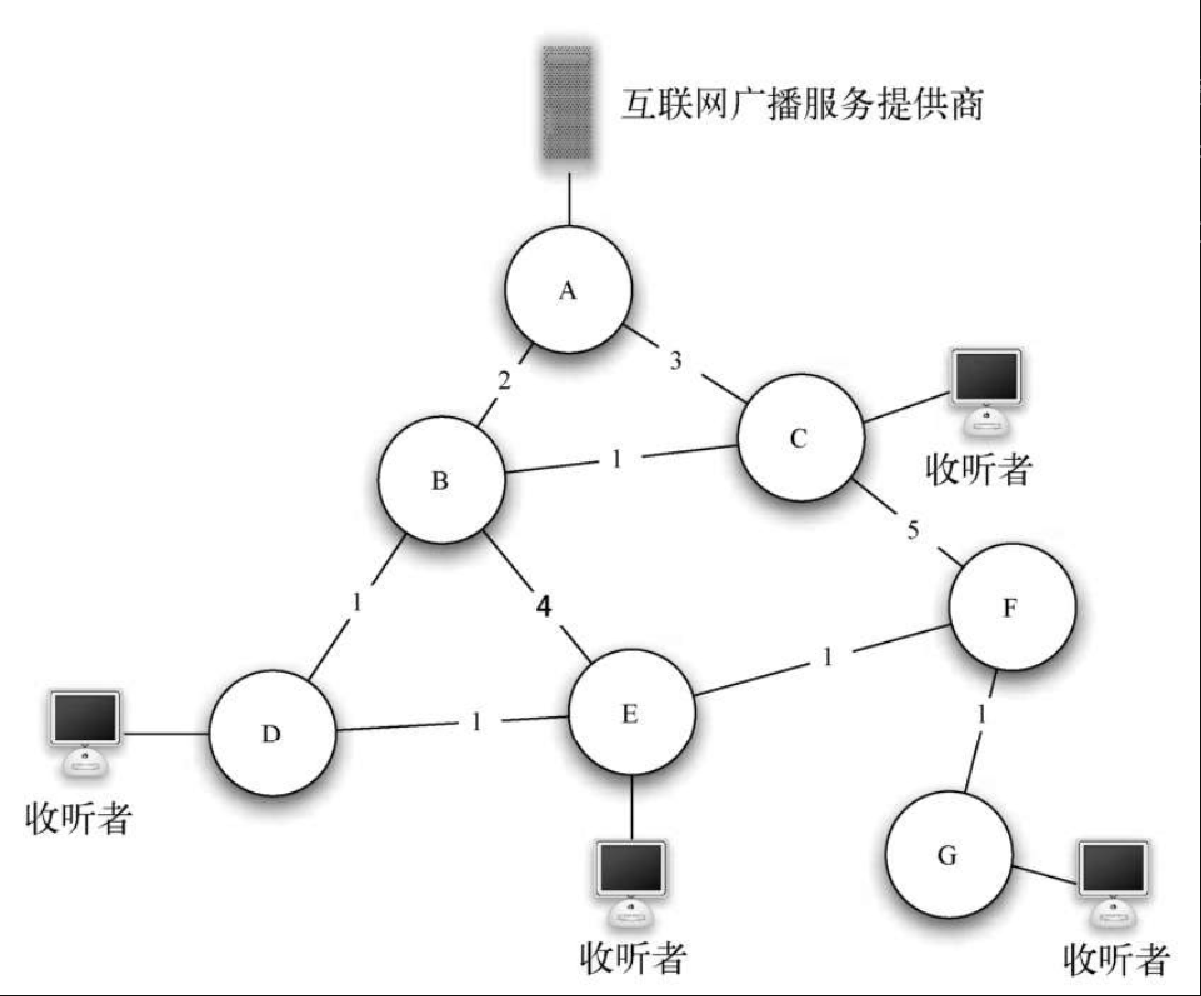
为了更好地理解上述问题，我们先来看看如何通过蛮力法求解。你稍后会看到，本节提出的解决方案为何优于蛮力法。假设互联网广播服务提供商要向所有收听者播放一条消息，最简单的方法是保存一份包含所有收听者的列表，然后向每一个收听者单独发送消息。以图7-31 为例，若采用上述解法，则每一条消息都需要有 4 份副本。假设使用开销最小的路径，让我们来看看每一个路由器需要处理多少次相同的消息。

从广播服务提供商发出的所有消息都会经过路由器 A，因此 A 能够看到每一条消息的所有副本。路由器 C 只能看到一份副本，而由于路由器 B 和 D 在收听者 1、2、3 的最短路径上，因此它们能够看到每一条消息的 3 份副本。考虑到广播服务提供商每秒会发送数百条消息，这样做会导致流量剧增。

一种蛮力法是广播服务提供商针对每条消息只发送一份副本，然后由路由器来正确地发送。最简单的方法就是无控制泛滥法，策略如下：每一条消息都设有存活时间 ttl，它大于或等于广播服务提供商和最远的收听者之间的距离；每一个路由器都接收到消息的一份副本，并且将消息发送给所有的相邻路由器。在消息被发送时，它的 ttl 递减，直到变为 0。不难发现，无控制泛滥法产生的不必要消息比第一种方法更多。

解决广播问题的关键在于构建一棵权重最小的生成树。我们对最小生成树的正式定义如下：对于图 \$G=(V, E)\$，最小生成树 T 是 E 的无环子集，并且连接 V 中的所有顶点。

图7-32 展示了简化的广播图，并且突出显示了形成最小生成树的所有边。为了解决广播问题，广播服务提供商只需向网络中发送一条消息副本。每一个路由器向属于生成树的相邻路由器转发消息，其中不包括刚刚向它发送消息的路由器。在图7-32 的例子中，A 把消息转发给 B, B 把消息转发给 C 和 D, D 转发给 E, E 转发给 F, F 转发给 G。每一个路由器都只看到任意消息的一份副本，并且所有的收听者都接收到了消息。

Figure 6. 图7-32 广播图中的最小生成树

上述思路对应的算法叫作 Prim 算法。由于每一步都选择代价最小的下一步，因此 Prim 算法属于一种 “贪婪算法”。在这个问题中，代价最小的下一步是选择权重最小的边。接下来实现 Prim 算法。

构建生成树的基本思想如下：

当 T 还不是生成树时，(a) 找到一条可以安全添加到树中的边；(b) 将新的边添加到 T 中。

难点在于，如何找到 “可以安全添加到树中的边”。我们这样定义安全的边：它的一端是生成树中的顶点，另一端是还不在生成树中的顶点。这保证了构建的树不会出现循环。

Prim 算法的 Python 实现如代码清单7-12 所示。与 Dijkstra 算法类似，Prim 算法也使用了优先级队列来选择下一个添加到图中的顶点。

代码清单7-12 Prim算法的Python实现

from pythonds.graphs import PriorityQueue, Graph, Vertex

def prim(G,start):
    pq = PriorityQueue()
    for v in G:
        v.setDistance(sys.maxsize)
        v.setPred(None)
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in G])
    while not pq.isEmpty():
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
          newCost = currentVert.getWeight(nextVert)
          if nextVert in pq and newCost<nextVert.getDistance():
              nextVert.setPred(currentVert)
              nextVert.setDistance(newCost)
              pq.decreaseKey(nextVert,newCost)

图7-33 展示了将 Prim 算法应用于示例生成树的过程。以顶点 A 作为起点，将 A 到其他所有顶点的距离都初始化为无穷大。检查 A 的相邻顶点后，可以更新从 A 到 B 和 C 的距离，因为实际的距离小于无穷大。更新距离之后，B 和 C 被移到优先级队列的头部。并且，它们的前驱顶点被设置为 A。注意，我们还没有把 B 和 C 添加到生成树中。只有在从优先级队列中移除时，顶点才会被添加到生成树中。

Figure 7. 图7-33 Prim算法的应用过程

由于到 B 的距离最短，因此接下来检查 B 的相邻顶点。检查后发现，可以更新 D 和 E。接下来处理优先级队列中的下一个顶点 C。与 C 相邻的唯一一个还在优先级队列中的顶点是 F，因此更新到 F 的距离，并且调整 F 在优先级队列中的位置。

现在检查与 D 相邻的顶点，发现可以将到 E 的距离从 6 减少为 4。修改距离的同时，把 E 的前驱顶点改为 D，以此准备将 E 添加到生成树中的另一个位置。Prim 算法正是通过这样的方式将每一个顶点都添加到生成树中。