动态规划
许多计算机程序被用于优化某些值,例如找到两点之间的最短路径,为一组数据点找到最佳拟合线,或者找到满足一定条件的最小对象集合。计算机科学家采用很多策略来解决这些问题。本书的一个目标就是帮助你了解不同的问题解决策略。在解决优化问题时,一个策略是 动态规划。
优化问题的一个经典例子就是在找零时使用最少的硬币。假设某个自动售货机制造商希望在每笔交易中给出最少的硬币。一个顾客使用一张一美元的纸币购买了价值 37 美分的物品,最少需要找给该顾客多少硬币呢?答案是 6 枚:25 美分的 2 枚,10 美分的 1 枚,1 美分的 3 枚。该如何计算呢?从面值最大的硬币(25 美分)开始,使用尽可能多的硬币,然后尽可能多地使用面值第 2 大的硬币。这种方法叫作贪婪算法——试图最大程度地解决问题。
对于美国的硬币来说,贪婪算法很有效。不过,假如除了常见的 1 分、5 分、10 分和 25 分,硬币的面值还有 21 分,那么贪婪算法就没法正确地为找零 63 分的情况得出最少硬币数。尽管多了 21 分的面值,贪婪算法仍然会得到 6 枚硬币的结果,而最优解是 3 枚面值为 21 分的硬币。
让我们来考察一种必定能得到最优解的方法。由于本章的主题是递归,因此你可能已经猜到,这是一种递归方法。首先确定基本情况:如果要找的零钱金额与硬币的面值相同,那么只需找 1 枚硬币即可。
如果要找的零钱金额和硬币的面值不同,则有多种选择:1 枚 1 分的硬币加上找零金额减去 1 分之后所需的硬币;1 枚 5 分的硬币加上找零金额减去 5 分之后所需的硬币;1 枚 10 分的硬币加上找零金额减去 10 分之后所需的硬币;1 枚 25 分的硬币加上找零金额减去 25 分之后所需的硬币。我们需要从中找到硬币数最少的情况,如下所示。
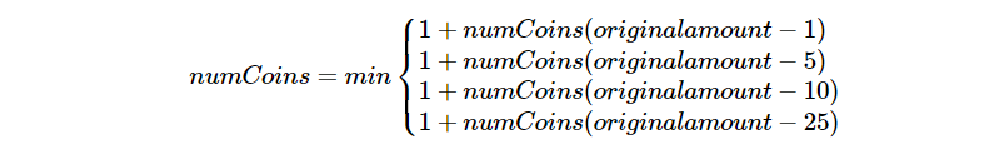
numCoins = min(1 + numCoins(originalamount -1),
1 + numCoins(originalamount -5),
1 + numCoins(originalamount -10),
1 + numCoins(originalamount -25))代码清单4-14 实现了上述算法。第3行检查是否为基本情况:尝试使用 1 枚硬币找零。如果没有一个硬币面值与找零金额相等,就对每一个小于找零金额的硬币面值进行递归调用。第 6 行使用列表循环来筛选出小于当前找零金额的硬币面值。第 7 行的递归调用将找零金额减去所选的硬币面值,并将所需的硬币数加 1,以表示使用了 1 枚硬币。
def recMC(coinValueList,change):
minCoins = change
if change in coinValueList:
return 1
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMC(coinValueList,change-i)
if numCoins < minCoins:
minCoins = numCoins
return minCoins
print(recMC([1,5,10,25],63))代码清单4-14 的问题是,它的效率非常低。事实上,针对找零金额是 63 分的情况,它需要进行 67716925 次递归调用才能找到最优解。图4-14 有助于理解该算法的严重缺陷。针对找零金额是 26 分的情况,该算法需要进行 377 次递归调用,图中仅展示了其中的一小部分。
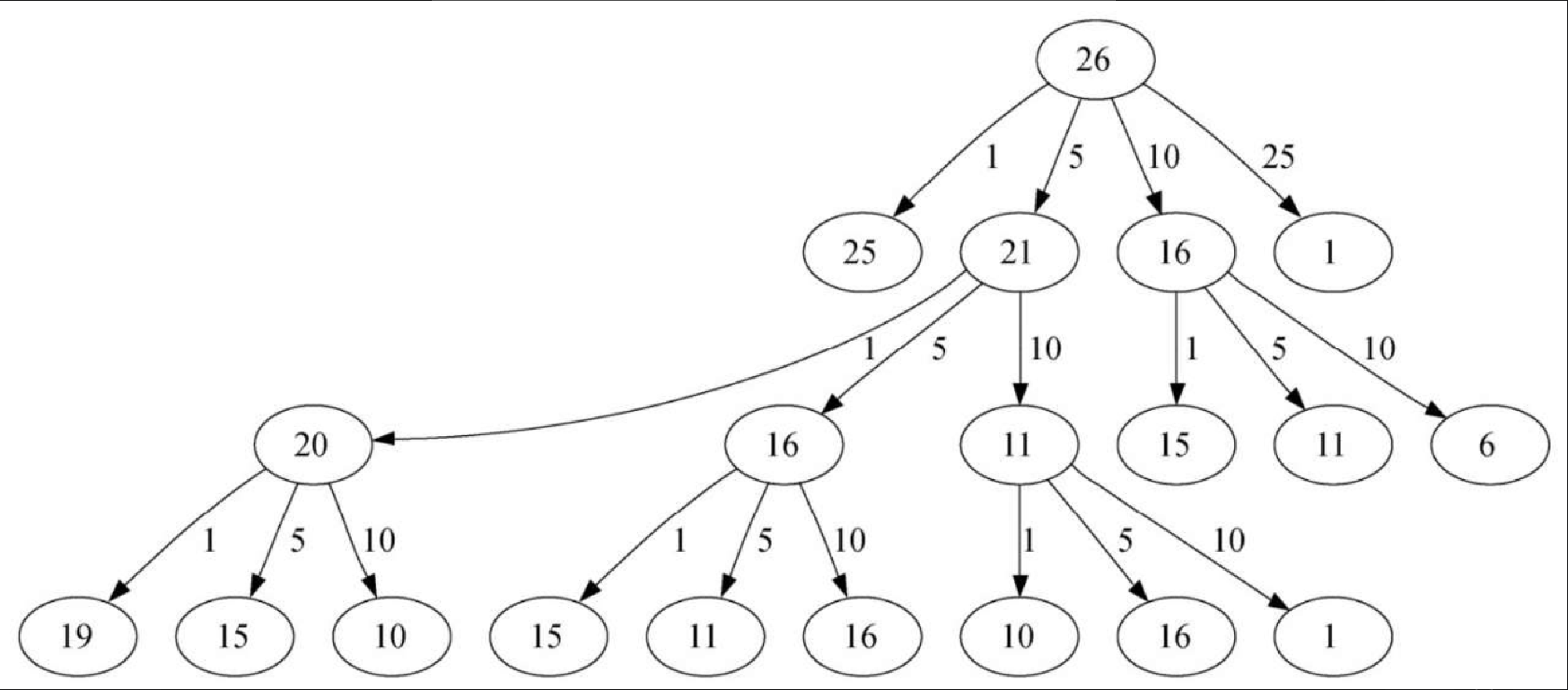
在图4-14 中,每一个节点都对应一次对 recMC 的调用,节点中的数字表示此时正在计算的找零金额,箭头旁的数字表示刚使用的硬币面值。从图中可以发现,采用不同的面值组合,可以到达任一节点。主要的问题是重复计算量太大。举例来说,数字为 15 的节点出现了 3 次,每次都会进行 52 次函数调用。显然,该算法将大量时间和资源浪费在了重复计算已有的结果上。
减少计算量的关键在于记住已有的结果。简单的做法是把最少硬币数的计算结果存储在一张表中,并在计算新的最少硬币数之前,检查结果是否已在表中。如果是,就直接使用结果,而不是重新计算。代码清单4-15 实现了添加查询表之后的算法。
def recDC(coinValueList,change,knownResults):
minCoins = change
if change in coinValueList:
knownResults[change] = 1
return 1
elif knownResults[change] > 0:
return knownResults[change]
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recDC(coinValueList, change-i,
knownResults)
if numCoins < minCoins:
minCoins = numCoins
knownResults[change] = minCoins
return minCoins
print(recDC([1,5,10,25],63,[0]*63))注意,第 6 行会检查查询表中是否已经有某个找零金额对应的最少硬币数。如果没有,就递归地计算并且把得到的最少硬币数结果存在表中。修改后的算法将计算找零 63 分所需的递归调用数降低到 221 次!
尽管代码清单4-15 实现的算法能得到正确的结果,但是它不太正规。如果查看 knownResults 表,会发现其中有一些空白的地方。事实上,我们所做的优化并不是动态规划,而是通过记忆化(或者叫作缓存)的方法来优化程序的性能。
真正的动态规划算法会用更系统化的方法来解决问题。在解决找零问题时,动态规划算法会从 1 分找零开始,然后系统地一直计算到所需的找零金额。这样做可以保证在每一步都已经知道任何小于当前值的找零金额所需的最少硬币数。
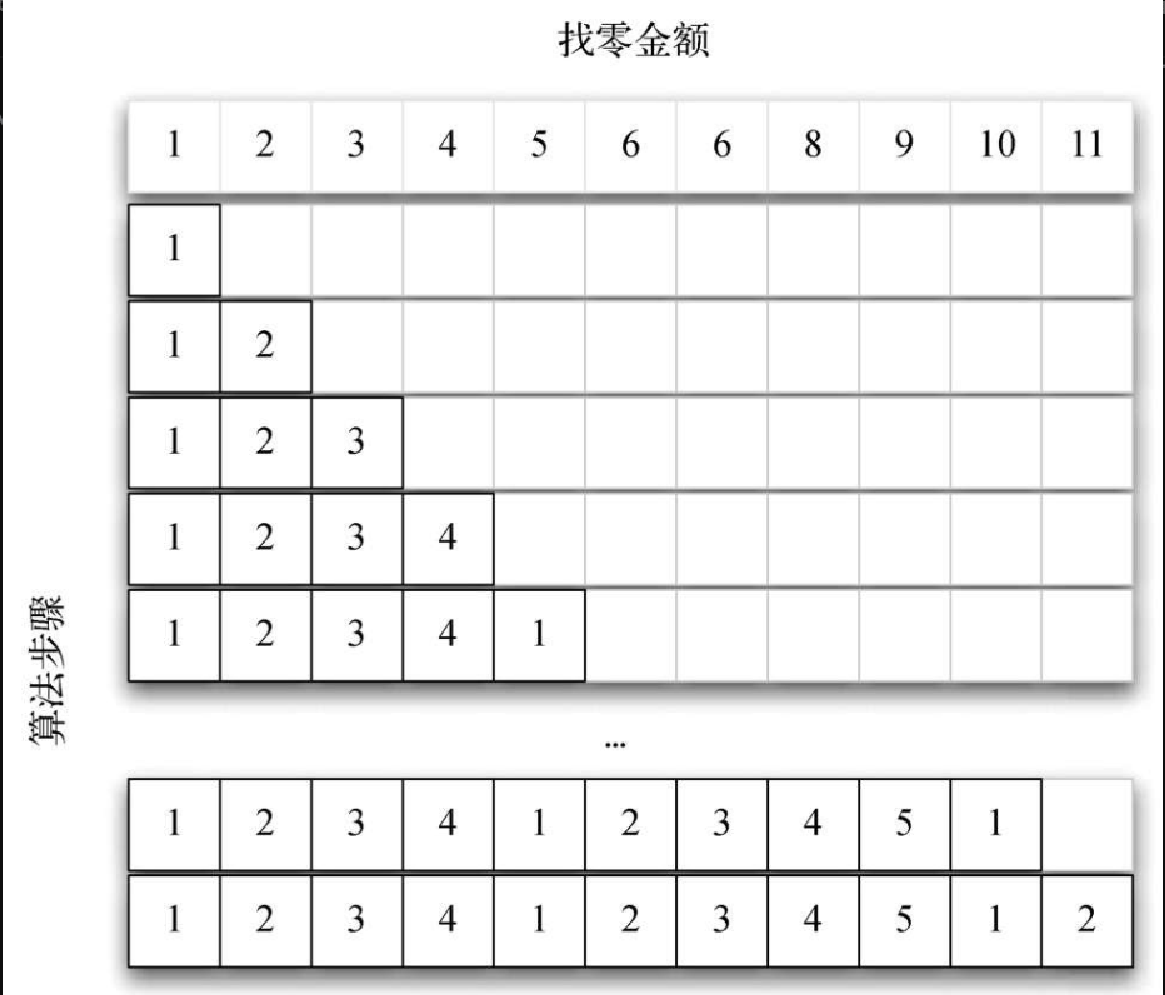
让我们来看看如何将找零 11 分所需的最少硬币数填入查询表,图4-15 展示了这个过程。从 1 分开始,只需找 1 枚 1 分的硬币。第 2 行展示了 1 分和 2 分所需的最少硬币数。同理,2 分只需找 2 枚 1 分的硬币。第 5 行开始变得有趣起来,此时我们有 2 个可选方案:要么找 5 枚 1 分的硬币,要么找 1 枚 5 分的硬币。哪个方案更好呢?查表后发现,4 分所需的最少硬币数是 4,再加上 1 枚 1 分的硬币就得到 5 分(共需要 5 枚硬币);如果直接找 1 枚 5 分的硬币,则最少硬币数是 1。由于 1 比 5 小,因此我们把 1 存入表中。接着来看 11 分的情况,我们有 3 个可选方案,如图4-16 所示。
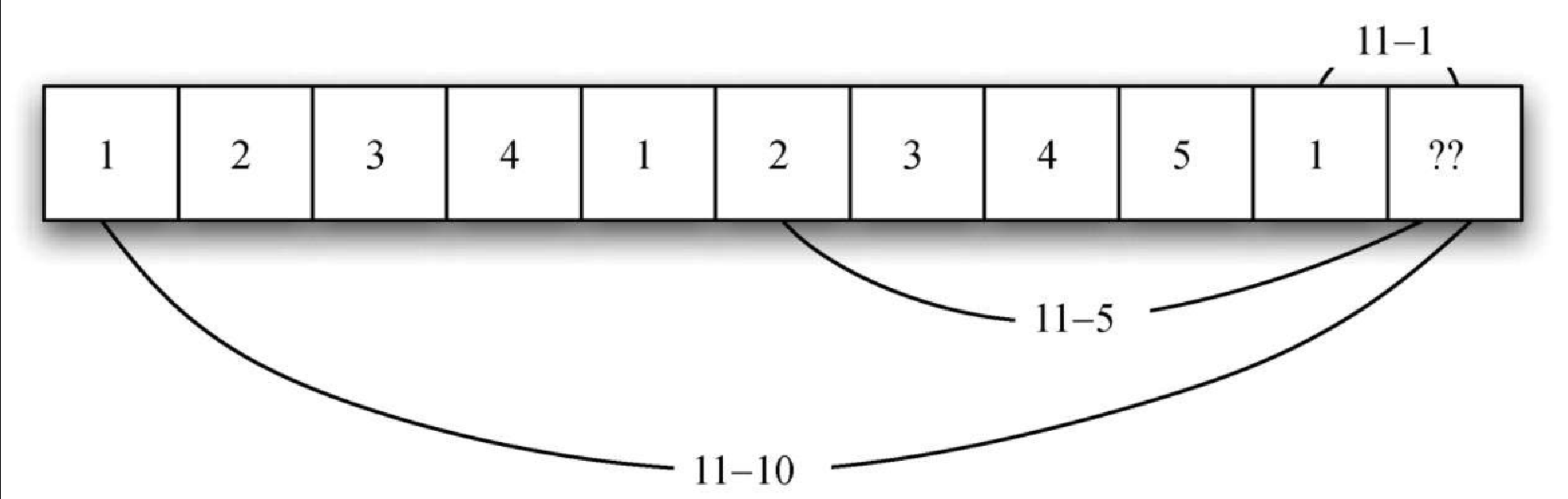
-
1 枚 1 分的硬币加上找 10 分零钱(11-1)最少需要的硬币(1枚)。
-
1 枚 5 分的硬币加上找 6 分零钱(11-5)最少需要的硬币(2枚)。
-
1 枚 10 分的硬币加上找 1 分零钱(11-10)最少需要的硬币(1枚)。
第 1 个和第 3 个方案均可得到最优解,即共需要 2 枚硬币。找零问题的动态规划解法如代码清单4-16 所示。dpMakeChange 接受 3 个参数:硬币面值列表、找零金额,以及由每一个找零金额所需的最少硬币数构成的列表。当函数运行结束时,minCoins 将包含找零金额从 0 到 change 的所有最优解。
def dpMakeChange(coinValueList,change,minCoins):
for cents in range(change+1):
coinCount = cents
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents-j] + 1 < coinCount:
coinCount = minCoins[cents-j]+1
minCoins[cents] = coinCount
return minCoins[change]注意,尽管我们一开始使用递归方法来解决找零问题,但是 dpMakeChange 并不是递归函数。请记住,能够用递归方法解决问题,并不代表递归方法是最好或最高效的方法。动态规划函数所做的大部分工作是从第 4 行开始的循环。该循环针对由 cents 指定的找零金额考虑所有可用的面值。和找零 11 分的例子一样,我们把最少硬币数记录在 minCoins 表中。
尽管找零算法在寻找最少硬币数时表现出色,但是由于没有记录所用的硬币,因此它并不能帮助我们进行实际的找零工作。通过记录 minCoins 表中每一项所加的硬币,可以轻松扩展 dpMakeChange,从而记录所用的硬币。如果知道上一次加的硬币,便可以减去其面值,从而找到表中前一项,并通过它知晓之前所加的硬币。代码清单4-17 展示了修改后的 dpMakeChange 算法,以及从表中回溯并打印所用硬币的 printCoins 函数。
def dpMakeChange(coinValueList,change,minCoins,coinsUsed):
for cents in range(change+1):
coinCount = cents
newCoin = 1
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents-j] + 1 < coinCount:
coinCount = minCoins[cents-j]+1
newCoin = j
minCoins[cents] = coinCount
coinsUsed[cents] = newCoin
return minCoins[change]
def printCoins(coinsUsed,change):
coin = change
while coin > 0:
thisCoin = coinsUsed[coin]
print(thisCoin)
coin = coin - thisCoin
def main():
amnt = 63
clist = [1,5,10,21,25]
coinsUsed = [0]*(amnt+1)
coinCount = [0]*(amnt+1)
print("Making change for",amnt,"requires")
print(dpMakeChange(clist,amnt,coinCount,coinsUsed),"coins")
print("They are:")
printCoins(coinsUsed,amnt)
print("The used list is as follows:")
print(coinsUsed)
main()最后,来看看动态规划算法如何处理硬币面值含 21 分的情况。前 3 行创建要使用的硬币列表。接着创建用来存储结果的列表。coinsUsed 是一个列表,其中是用于找零的硬币。coinCount 是最少硬币数。
>>> cl = [1, 5, 10, 21, 25]
>>> coinsUsed = [0]*64
>>> coinCount = [0]*64
>>> dpMakeChange(cl, 63, coinCount, coinsUsed)
3
>>> printCoins(coinsUsed, 63)
21
21
21
>>> printCoins(coinsUsed, 52)
10
21
21
>>> coinsUsed
[1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 1, 1, 1, 1, 5, 1, 1, 1, 1,
10, 21, 1, 1, 1, 25, 1, 1, 1, 1, 5, 10, 1, 1, 1, 10, 1, 1, 1,
1, 5, 10, 21, 1, 1, 10, 21, 1, 1, 1, 25, 1, 10, 1, 1, 5, 10,
1, 1, 1, 10, 1, 10, 21]注意,硬币的打印结果直接取自 coinsUsed。第一次调用 printCoins 时,从 coinsUsed 的位置 63 处开始,打印出 21;然后计算 63-21=42,接着查看列表的第 42 个元素。这一次,又遇到了 21。最后,第 21 个元素也是 21。由此,便得到 3 枚 21 分的硬币。