小结

本章探讨了递归算法的一些例子。选择这些算法，是为了让你理解递归能高效地解决何种问题。以下是本章的要点。

所有递归算法都必须有基本情况。
递归算法必须改变其状态并向基本情况靠近。
递归算法必须递归地调用自己。
递归在某些情况下可以替代循环。
递归算法往往与问题的形式化表达相对应。
递归并非总是最佳方案。有时，递归算法比其他算法的计算复杂度更高。

讨论题

画出汉诺塔问题的调用栈（假设起初栈中有3个盘子）。
根据 4.4 节所描述的规则，在纸上绘制出谢尔平斯基三角形。
采用动态规划算法找零，计算找零 33 美分所需的最少硬币数（假设除了常见的面值外，还有面值为 8 美分的硬币）。

编程练习

写一个递归函数来计算数的阶乘。
写一个递归函数来反转列表。
采用下列一个或全部方法修改递归树程序。
- 修改树枝的粗细程度，使得 branchLen 越小，线条越细。
- 修改树枝的颜色，使得当 branchLen 非常小时，树枝看上去像叶子。
- 修改小乌龟的转向角度，使得每一个分支的角度都是一定范围内的随机值，例如使角度取值范围是 15～45 度。运行程序，查看绘制结果。
- 递归地修改 branchLen，使其减去一定范围内的随机值，而不是固定值。
找到一种绘制分形山的算法。提示：可以使用三角形。
写一个递归函数来计算斐波那契数列，并对比递归函数与循环函数的性能。
实现汉诺塔问题的一个解决方案，使用 3 个栈来记录盘子的位置。
使用 turtle 绘图模块写一个递归程序，画出希尔伯特曲线。
使用 turtle 绘图模块写一个递归程序，画出科赫雪花。
写一个程序来解决这样一个问题：有 2 个坛子，其中一个的容量是 4 加仑，另一个的是 3 加仑。坛子上都没有刻度线。可以用水泵将它们装满水。如何使 4 加仑的坛子最后装有 2 加仑的水？
扩展练习 9 中的程序，将坛子的容量和较大的坛子中最后的水量作为参数。
写一个程序来解决这样一个问题：3 只羚羊和 3 只狮子准备乘船过河，河边有一艘能容纳 2 只动物的小船。但是，如果两侧河岸上的狮子数量大于羚羊数量，羚羊就会被吃掉。找到运送办法，使得所有动物都能安全渡河。
利用 turtle 绘图模块修改汉诺塔程序，将盘子的移动过程可视化。提示：可以创建多只小乌龟，并将它们的形状改为长方形。
帕斯卡三角形由数字组成，其中的数字交错摆放，使得：11 11 21 13 3114 64 1

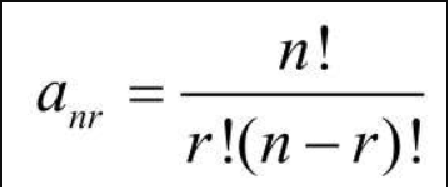
这是计算二项式系数的等式。在帕斯卡三角形中，每个数等于其上方两数之和，如下所示。

将行数作为参数，写一个输出帕斯卡三角形的程序。
假设一个计算机科学家兼艺术大盗闯入美术馆。他只能用一个容量为 W 磅的背包来装盗取的艺术品，并且他对每一件艺术品的价值和重量了如指掌。他会如何写一个动态规划程序来帮助自己最大程度地获利呢？下面的例子可以帮助你思考：假设背包容量是 20 磅，艺术品为 5 件。
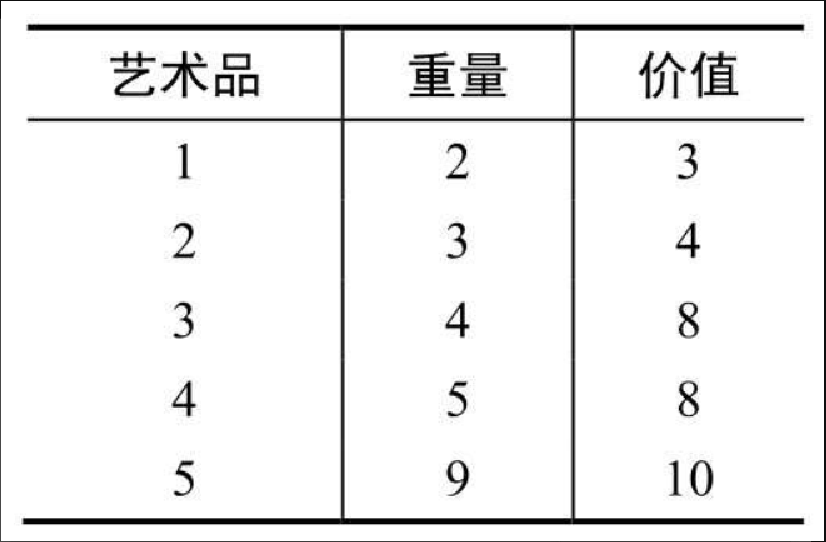
请尝试解决字符串编辑距离问题，它在很多研究领域中非常有用。假设要把单词 algorithm 转换成 alligator。对于每一个字母，可以用 5 个单位的代价将其从一个单词复制到另一个，也可以用 20 个单位的代价将其删除或插入。拼写检查程序利用将一个单词转换为另一个的总代价来提供拼写建议。请设计一个动态规划算法，给出任意两个单词之间的最小编辑距离。