二叉树的应用

解析树

树的实现已经齐全了，现在来看看如何用树解决一些实际问题。本节介绍解析树，可以用它来表示现实世界中像句子（如图 6-9 所示）或数学表达式这样的构造。

Figure 1. 图6-9 一个简单句子的解析树

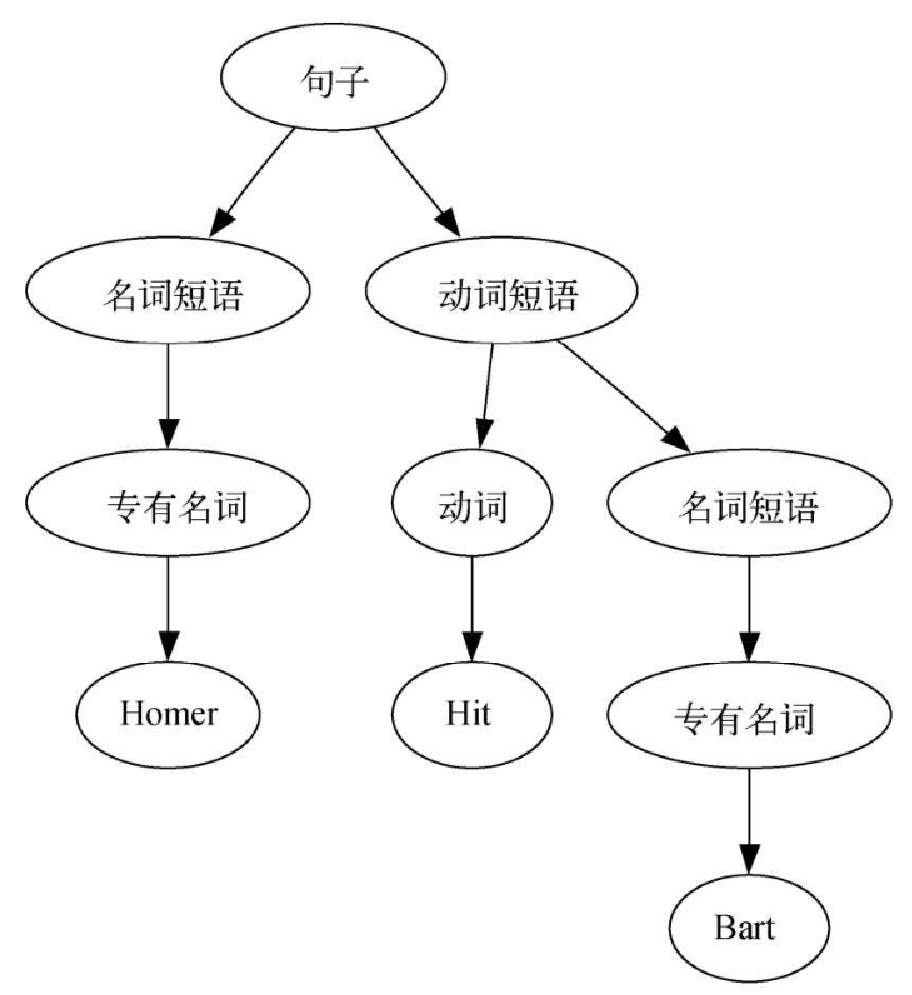
图6-9 展示了一个简单句子的层次结构。用树状结构表示句子让我们可以使用子树处理句子的独立部分。

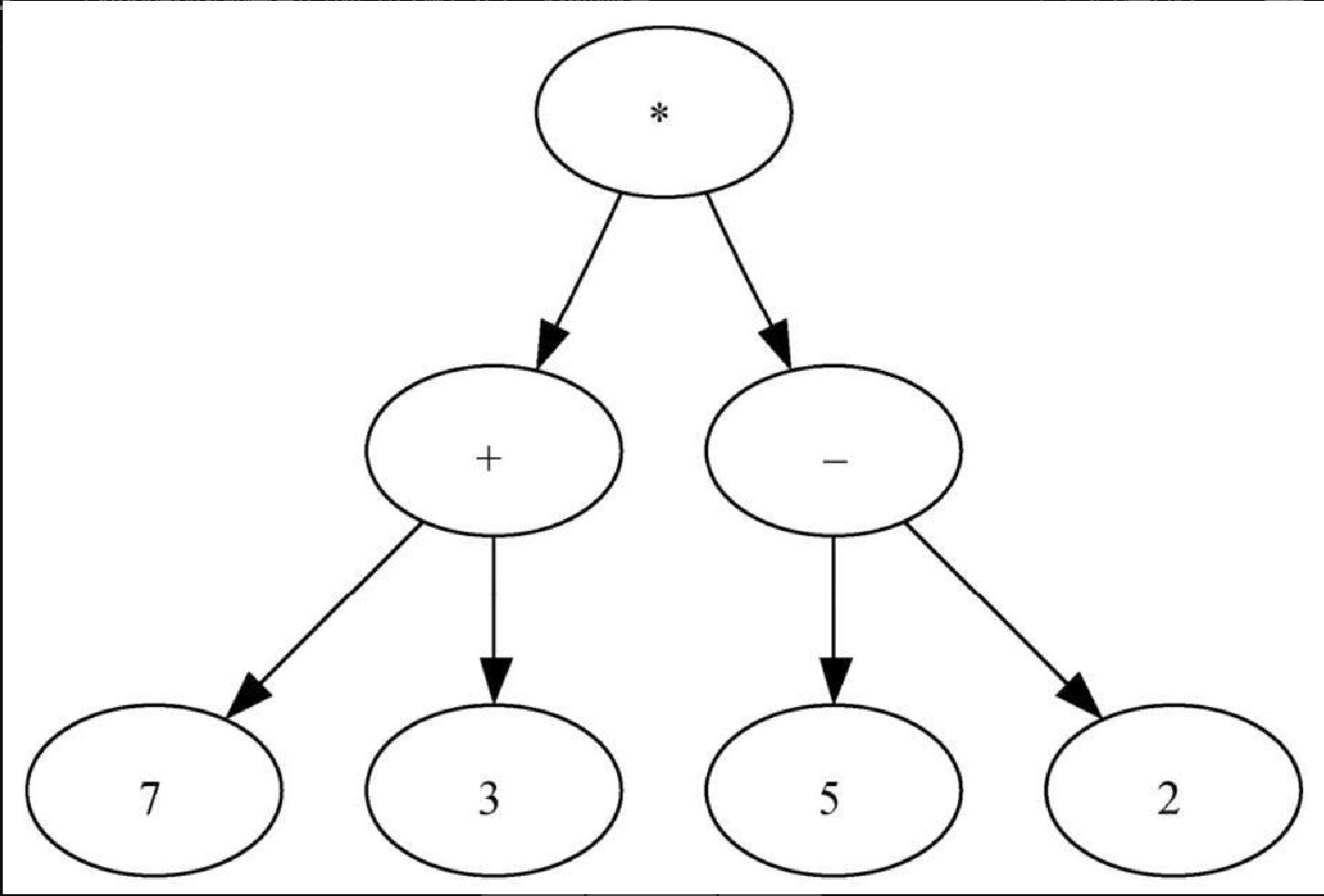
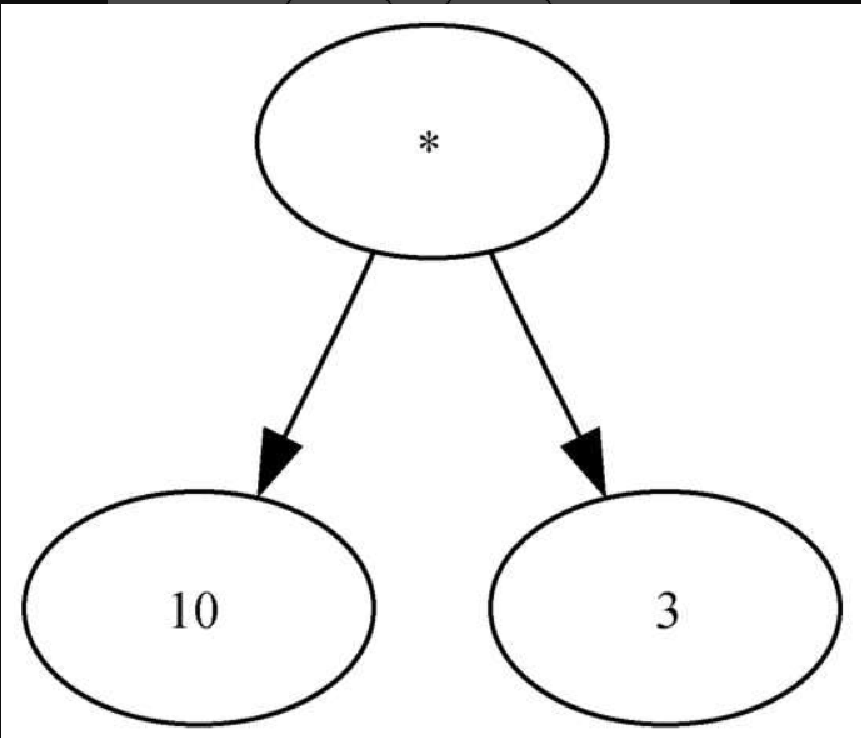
我们也可以将 7 + 3) ∗ (5 - 2 这样的数学表达式表示成解析树，如图6-10 所示。这是完全括号表达式，乘法的优先级高于加法和减法，但因为有括号，所以在做乘法前必须先做括号内的加法和减法。树的层次性有助于理解整个表达式的计算次序。在计算顶层的乘法前，必须先计算子树中的加法和减法。加法（左子树）的结果是 10，减法（右子树）的结果是 3。利用树的层次结构，在计算完子树的表达式后，只需用一个节点代替整棵子树即可。应用这个替换过程后，便得到如图 6-11 所示的简化树。

Figure 2. 图6-10 7 + 3) ∗ (5-2的解析树

Figure 3. 图6-11 7 + 3) ∗ (5-2的简化解析树

本节的剩余部分将仔细考察解析树，重点如下：

如何根据完全括号表达式构建解析树；
如何计算解析树中的表达式；
如何将解析树还原成最初的数学表达式。

构建解析树的第一步是将表达式字符串拆分成标记列表。需要考虑4种标记：左括号、右括号、运算符和操作数。我们知道，左括号代表新表达式的起点，所以应该创建一棵对应该表达式的新树。反之，遇到右括号则意味着到达该表达式的终点。我们也知道，操作数既是叶子节点，也是其运算符的子节点。此外，每个运算符都有左右子节点。

有了上述信息，便可以定义以下4条规则：

如果当前标记是 (，就为当前节点添加一个左子节点，并下沉至该子节点；
如果当前标记在列表 ['+', '-', '/', '*'] 中，就将当前节点的值设为当前标记对应的运算符；为当前节点添加一个右子节点，并下沉至该子节点；
如果当前标记是数字，就将当前节点的值设为这个数并返回至父节点；
如果当前标记是 )，就跳到当前节点的父节点。

编写 Python 代码前，我们先通过一个例子来理解上述规则。将表达式 (3 + (4 ∗ 5)) 拆分成标记列表 ['(', '3', '+', '(', '4', '*', '5', ')', ')']。起初，解析树只有一个空的根节点，随着对每个标记的处理，解析树的结构和内容逐渐充实，如图 6-12 所示。

Figure 4. 图6-12 一步步地构建解析树

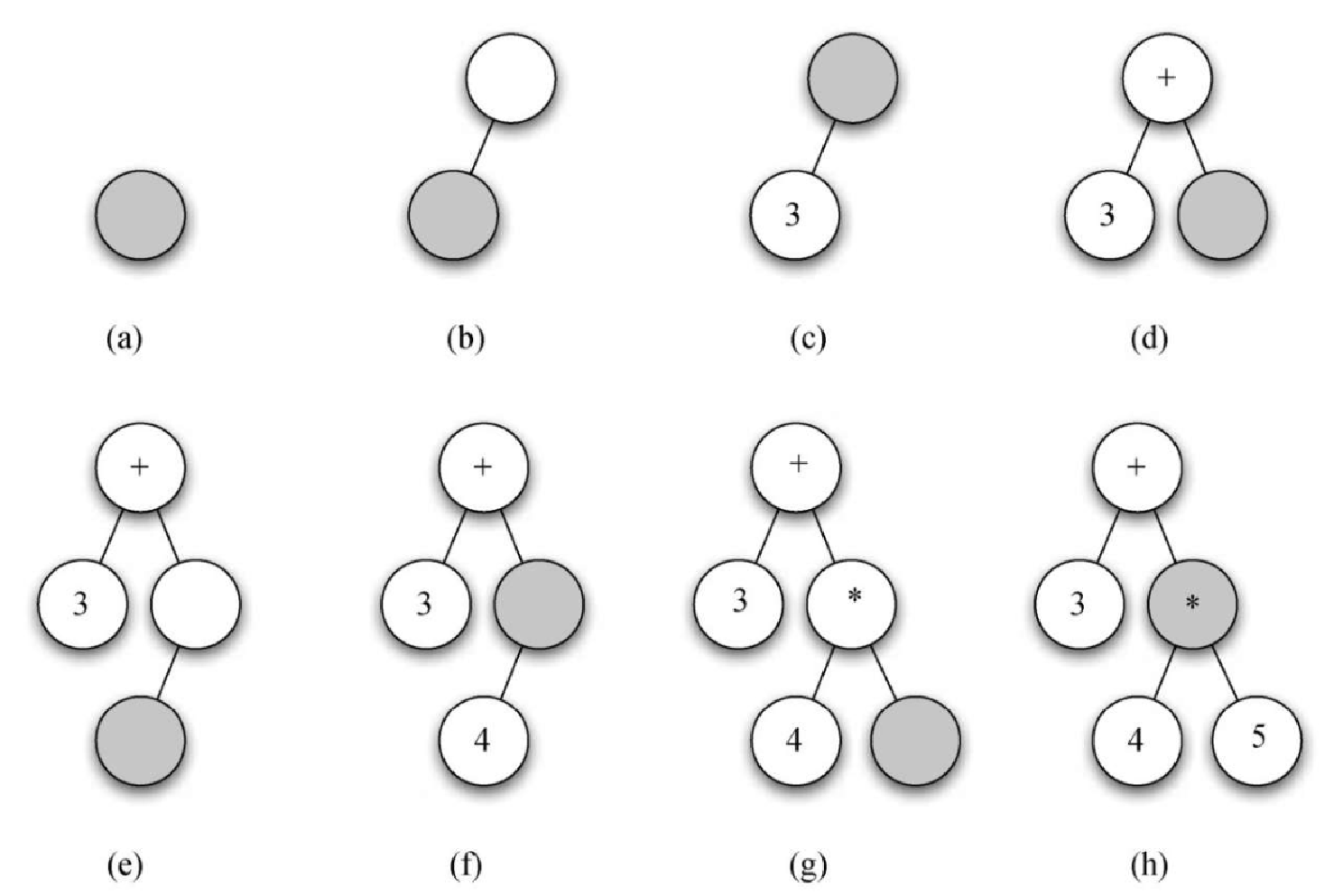
以图 6-12 为例，我们来一步步地构建解析树。

创建一棵空树。
读入第一个标记 (。根据规则 1，为根节点添加一个左子节点。
读入下一个标记 3。根据规则 3，将当前节点的值设为 3，并回到父节点。
读入下一个标记 +。根据规则 2，将当前节点的值设为 +，并添加一个右子节点。新节点成为当前节点。
读入下一个标记 (。根据规则 1，为当前节点添加一个左子节点，并将其作为当前节点。
读入下一个标记 4。根据规则 3，将当前节点的值设为 4，并回到父节点。
读入下一个标记 *。根据规则 2，将当前节点的值设为 *，并添加一个右子节点。新节点成为当前节点。
读入下一个标记 5。根据规则 3，将当前节点的值设为 5，并回到父节点。
读入下一个标记 )。根据规则 4，将 * 的父节点作为当前节点。
读入下一个标记 )。根据规则 4，将 + 的父节点作为当前节点。因为 + 没有父节点，所以工作完成。

本例表明，在构建解析树的过程中，需要追踪当前节点及其父节点。可以通过 getLeftChild 与 getRightChild 获取子节点，但如何追踪父节点呢？一个简单的办法就是在遍历这棵树时使用栈记录父节点。每当要下沉至当前节点的子节点时，先将当前节点压到栈中。当要返回到当前节点的父节点时，就将父节点从栈中弹出来。

利用前面描述的规则以及 Stack 和 BinaryTree，就可以编写创建解析树的 Python 函数。代码清单 6-9 给出了解析树构建器的代码。

代码清单6-9 解析树构建器

from pythonds.basic import Stack
from pythonds.trees import BinaryTree

def buildParseTree(fpexp):
    fplist = fpexp.split()
    pStack = Stack()
    eTree = BinaryTree('')
    pStack.push(eTree)
    currentTree = eTree

    for i in fplist:
        if i == '(':
            currentTree.insertLeft('')
            pStack.push(currentTree)
            currentTree = currentTree.getLeftChild()

        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i)
            currentTree.insertRight('')
            pStack.push(currentTree)
            currentTree = currentTree.getRightChild()

        elif i == ')':
            currentTree = pStack.pop()

        elif i not in ['+', '-', '*', '/', ')']:
            try:
                currentTree.setRootVal(int(i))
                parent = pStack.pop()
                currentTree = parent

            except ValueError:
                raise ValueError("token '{}' is not a valid integer".format(i))

    return eTree

pt = buildParseTree("( ( 10 + 5 ) * 3 )")
pt.postorder()  #defined and explained in the next section

在代码清单 6-9 中，第 11、15、19 和 24 行的 if 语句体现了构建解析树的 4 条规则，其中每条语句都通过调用 BinaryTree 和 Stack 的方法实现了前面描述的规则。这个函数中唯一的错误检查在 else 从句中，如果遇到一个不能识别的标记，就抛出一个 ValueError 异常。

有了一棵解析树之后，我们能对它做些什么呢？作为第一个例子，我们可以写一个函数计算解析树，并返回计算结果。要写这个函数，我们将利用树的层次性。针对图 6-10 中的解析树，可以用图 6-11 中的简化解析树替换。由此可见，可以写一个算法，通过递归计算每棵子树得到整棵解析树的结果。

和之前编写递归函数一样，设计递归计算函数要从确定基本情况开始。就针对树进行操作的递归算法而言，一个很自然的基本情况就是检查叶子节点。解析树的叶子节点必定是操作数。由于像整数和浮点数这样的数值对象不需要进一步翻译，因此 evaluate 函数可以直接返回叶子节点的值。为了向基本情况靠近，算法将执行递归步骤，即对当前节点的左右子节点调用 evaluate 函数。递归调用可以有效地沿着各条边往叶子节点靠近。

若要结合两个递归调用的结果，只需将父节点中存储的运算符应用于子节点的计算结果即可。从图 6-11 中可知，根节点的两个子节点的计算结果就是它们自身，即 10 和 3。应用乘号，得到最后的结果 30。

递归函数 evaluate 的实现如代码清单 6-10 所示。首先，获取指向当前节点的左右子节点的引用。如果左右子节点的值都是 None，就说明当前节点确实是叶子节点。第 7 行执行这项检查。如果当前节点不是叶子节点，则查看当前节点中存储的运算符，并将其应用于左右子节点的递归计算结果。

代码清单6-10 计算二叉解析树的递归函数

import operator
def evaluate(parseTree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}

    leftC = parseTree.getLeftChild()
    rightC = parseTree.getRightChild()

    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        return fn(evaluate(leftC),evaluate(rightC))
    else:
        return parseTree.getRootVal()

我们使用具有键 +、-、* 和 / 的字典实现。字典中存储的值是 operator 模块的函数。该模块给我们提供了常用运算符的函数版本。在字典中查询运算符时，对应的函数对象被取出。既然取出的对象是函数，就可以用普通的方式 function(param1,param2) 调用。因此，opers['+'](2, 2) 等价于 operator.add(2, 2)。

最后，让我们通过图 6-12 中的解析树构建过程来理解 evaluate 函数。第一次调用 evaluate 函数时，将整棵树的根节点作为参数 parseTree 传入。然后，获取指向左右子节点的引用，检查它们是否存在。第 9 行进行递归调用。从查询根节点的运算符开始，该运算符是 +，对应 operator.add 函数，要传入两个参数。和普通的 Python 函数调用一样，Python 做的第一件事是计算入参的值。本例中，两个入参都是对 evaluate 函数的递归调用。由于入参的计算顺序是从左到右，因此第一次递归调用是在左边。对左子树递归调用 evaluate 函数，发现节点没有左右子节点，所以这是一个叶子节点。处于叶子节点时，只需返回叶子节点的值作为计算结果即可。本例中，返回整数 3。

至此，我们已经为顶层的 operator.add 调用计算出一个参数的值了，但还没完。继续从左到右的参数计算过程，现在进行一个递归调用，计算根节点的右子节点。我们发现，该节点不仅有左子节点，还有右子节点，所以检查节点存储的运算符——是 *，将左右子节点作为参数调用函数。这时可以看到，两个调用都已到达叶子节点，计算结果分别是 4 和 5。算出参数之后，返回 operator.mul(4, 5) 的结果。至此，我们已经算出了顶层运算符（+）的操作数，剩下的工作就是完成对 operator.add(3, 20) 的调用。因此，表达式 (3 + (4 ∗ 5)) 的计算结果就是 23。

树的遍历

我们已经了解了树的基本功能，现在是时候看看一些附加的使用模式了。这些使用模式可以按节点的访问方式分为 3 种。我们将对所有节点的访问称为 “遍历”，共有3种遍历方式，分别为前序遍历、中序遍历和后序遍历。接下来，我们先仔细地定义这 3 种遍历方式，然后通过一些例子看看它们的用法。

前序遍历: 在前序遍历中，先访问根节点，然后递归地前序遍历左子树，最后递归地前序遍历右子树。
中序遍历: 在中序遍历中，先递归地中序遍历左子树，然后访问根节点，最后递归地中序遍历右子树。
后序遍历: 在后序遍历中，先递归地后序遍历右子树，然后递归地后序遍历左子树，最后访问根节点。

让我们通过几个例子来理解这 3 种遍历方式。首先看看前序遍历。我们将一本书的内容结构表示为一棵树，整本书是根节点，每一章是根节点的子节点，每一章中的每一节是这章的子节点，每小节又是这节的子节点，依此类推。图 6-13 展示了一本书的树状结构，它包含两章。注意，遍历算法对每个节点的子节点数没有要求，但本例只针对二叉树。

Figure 5. 图6-13 一本书的树状结构

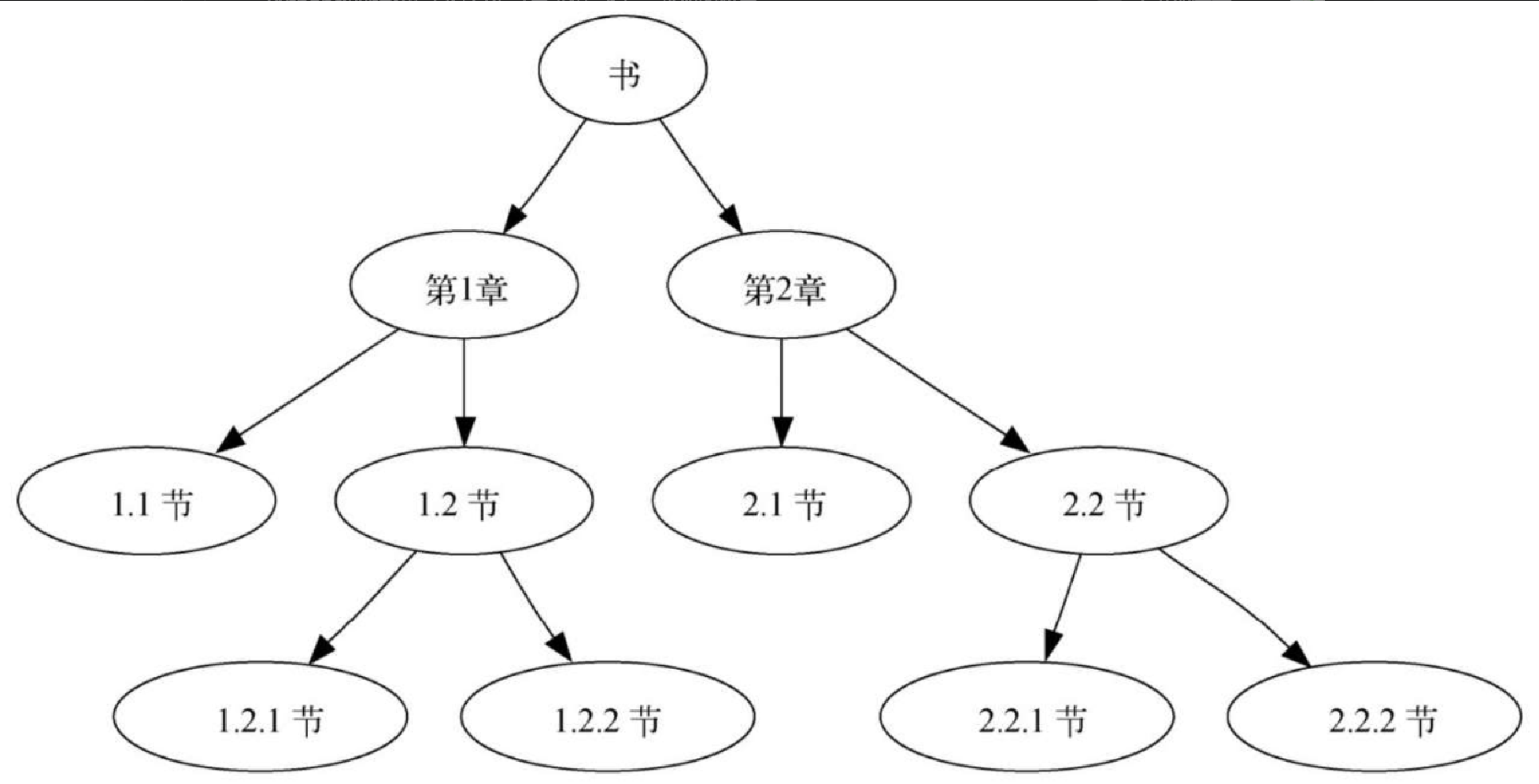
假设我们从前往后阅读这本书，那么阅读顺序就符合前序遍历的次序。从根节点 “书” 开始，遵循前序遍历指令，对左子节点 “第1章” 递归调用 preorder 函数。然后，对 “第1章” 的左子节点递归调用 preorder 函数，得到节点 “1.1节”。由于该节点没有子节点，因此不必再进行递归调用。沿着树回到节点 “第1章”，接下来访问它的右子节点，即 “1.2节”。和前面一样，先访问左子节点 “1.2.1节”，然后访问右子节点 “1.2.2节”。访问完 “1.2节” 之后，回到 “第1章”。接下来，回到根节点，以同样的方式访问节点 “第2章”。

遍历树的代码格外简洁，这主要是因为遍历是递归的。

你可能会想，前序遍历算法的最佳实现方式是什么呢？是一个将树用作数据结构的函数，还是树本身的一个方法？代码清单 6-11 给出了前序遍历算法的外部函数版本，该函数将二叉树作为参数，其代码尤为简洁，这是因为算法的基本情况仅仅是检查树是否存在。如果参数 tree 是 None，函数直接返回。

代码清单6-11 将前序遍历算法实现为外部函数

def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild())

我们也可以将 preorder 实现为 BinaryTree 类的方法，如代码清单 6-12 所示。请留意将代码从外部移到内部后有何变化。通常来说，不仅需要用 self 代替 tree，还需要修改基本情况。内部方法必须在递归调用 preorder 前，检查左右子节点是否存在。

代码清单6-12 将前序遍历算法实现为BinaryTree类的方法

def preorder(self):
    print(self.key)
    if self.leftChild:
        self.leftChild.preorder()
    if self.rightChild:
        self.rightChild.preorder()

哪种实现方式更好呢？在本例中，将 preorder 实现为外部函数可能是更好的选择。原因在于，很少会仅执行遍历操作，在大多数情况下，还要通过基本的遍历模式实现别的目标。在下一个例子中，我们就会通过后序遍历来计算解析树。所以，我们在此采用外部函数版本。

在代码清单 6-13 中，后序遍历函数 postorder 与前序遍历函数 preorder 几乎相同，只不过对 print 的调用被移到了函数的末尾。

代码清单6-13 后序遍历函数

def postorder(tree):
    if tree != None:
        postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
        print(tree.getRootVal())

我们已经见识过后序遍历的一个常见用途，那就是计算解析树。回顾代码清单 6-10，我们所做的就是先计算左子树，再计算右子树，最后通过根节点运算符的函数调用将两个结果结合起来。假设二叉树只存储一个表达式的数据。让我们来重写计算函数，使之更接近于代码清单 6-13 中的后序遍历函数。

代码清单6-14 后序求值函数

def postordereval(tree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}
    res1 = None
    res2 = None
    if tree:
        res1 = postordereval(tree.getLeftChild())
        res2 = postordereval(tree.getRightChild())
        if res1 and res2:
            return opers[tree.getRootVal()](res1,res2)
        else:
            return tree.getRootVal()

注意，代码清单 6-14 与代码清单 6-13 在形式上很相似，只不过求值函数最后不是打印节点，而是返回节点。这样一来，就可以保存从第 7 行和第 8 行的递归调用返回的值，然后在第 10 行使用这些值和运算符进行计算。

最后来了解中序遍历。中序遍历的访问顺序是左子树、根节点、右子树。代码清单 6-15 给出了中序遍历函数的代码。注意，3 个遍历函数的区别仅在于 print 语句与递归调用语句的相对位置。

代码清单6-15 中序遍历函数

def inorder(tree):
  if tree != None:
      inorder(tree.getLeftChild())
      print(tree.getRootVal())
      inorder(tree.getRightChild())

通过中序遍历解析树，可以还原不带括号的表达式。接下来修改中序遍历算法，以得到完全括号表达式。唯一要做的修改是：在递归调用左子树前打印一个左括号，在递归调用右子树后打印一个右括号。代码清单 6-16 是修改后的函数。

代码清单6-16 修改后的中序遍历函数，它能还原完全括号表达式

def printexp(tree):
  sVal = ""
  if tree:
      sVal = '(' + printexp(tree.getLeftChild())
      sVal = sVal + str(tree.getRootVal())
      sVal = sVal + printexp(tree.getRightChild())+')'
  return sVal

以下 Python 会话展示了 printexp 和 postordereval 的用法。

>>> from pythonds.trees import BinaryTree
>>> x = BinaryTree('*')
>>> x.insertLeft('+')
>>> l = x.getLeftChild()
>>> l.insertLeft(4)
>>> l.insertRight(5)
>>> x.insertRight(7)
>>>
>>> print(printexp(x))
(((4) + (5)) * (7))
>>>
>>> print(postordereval(x))
63
>>>

注意，printexp 函数给每个数字都加上了括号。尽管不能算错误，但这些括号显然是多余的。在章末的练习中，请修改 printexp 函数，移除这些括号。