小结

本章介绍了树这一数据结构。有了树，我们可以写出很多有趣的算法。我们用树做了以下这些事。

  • 用二叉树解析并计算表达式。

  • 用二叉树实现映射。

  • 用平衡二叉树（AVL 树）实现映射。

  • 用二叉树实现最小堆。

  • 用最小堆实现优先级队列。

讨论题

  1. 画出下列函数调用后的树结构。

    >>> r = BinaryTree(3)
>>> insertLeft(r, 4)
[3, [4, [], []], []]
>>> insertLeft(r, 5)
[3, [5, [4, [], []], []], []]
>>> insertRight(r, 6)
[3, [5, [4, [], []], []], [6, [], []]]
>>> insertRight(r, 7)
[3, [5, [4, [], []], []], [7, [], [6, [], []]]]
>>> setRootVal(r, 9)
>>> insertLeft(r, 11)
[9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]

  2. 为表达式 (4 * 8) / 6-3 创建对应的表达式树。

  3. 针对整数列表 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]，给出插入列表中整数得到的二叉搜索树。

  4. 针对整数列表 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]，给出插入列表中整数得到的二叉搜索树。

  5. 生成一个随机整数列表。给出插入列表中整数得到的二叉堆。

  6. 将前一道题得到的列表作为 buildHeap 方法的参数，给出得到的二叉堆。以树和列表两种形式展示。

  7. 画出按次序插入这些键之后的二叉搜索树：68、88、61、89、94、50、4、76、66、82。

  8. 生成一个随机整数列表。画出插入列表中整数得到的二叉搜索树。

  9. 针对整数列表 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]，给出插入列表中整数得到的二叉堆。

  10. 针对整数列表 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]，给出插入列表中整数得到的二叉堆。

  11. 考虑本章实现二叉树的两种方式。在实现为方法时，为什么必须在调用 preorder 前检查，而在实现为函数时，可以在调用内部检查？

  12. 给出构建下面这棵二叉树所需的函数调用。

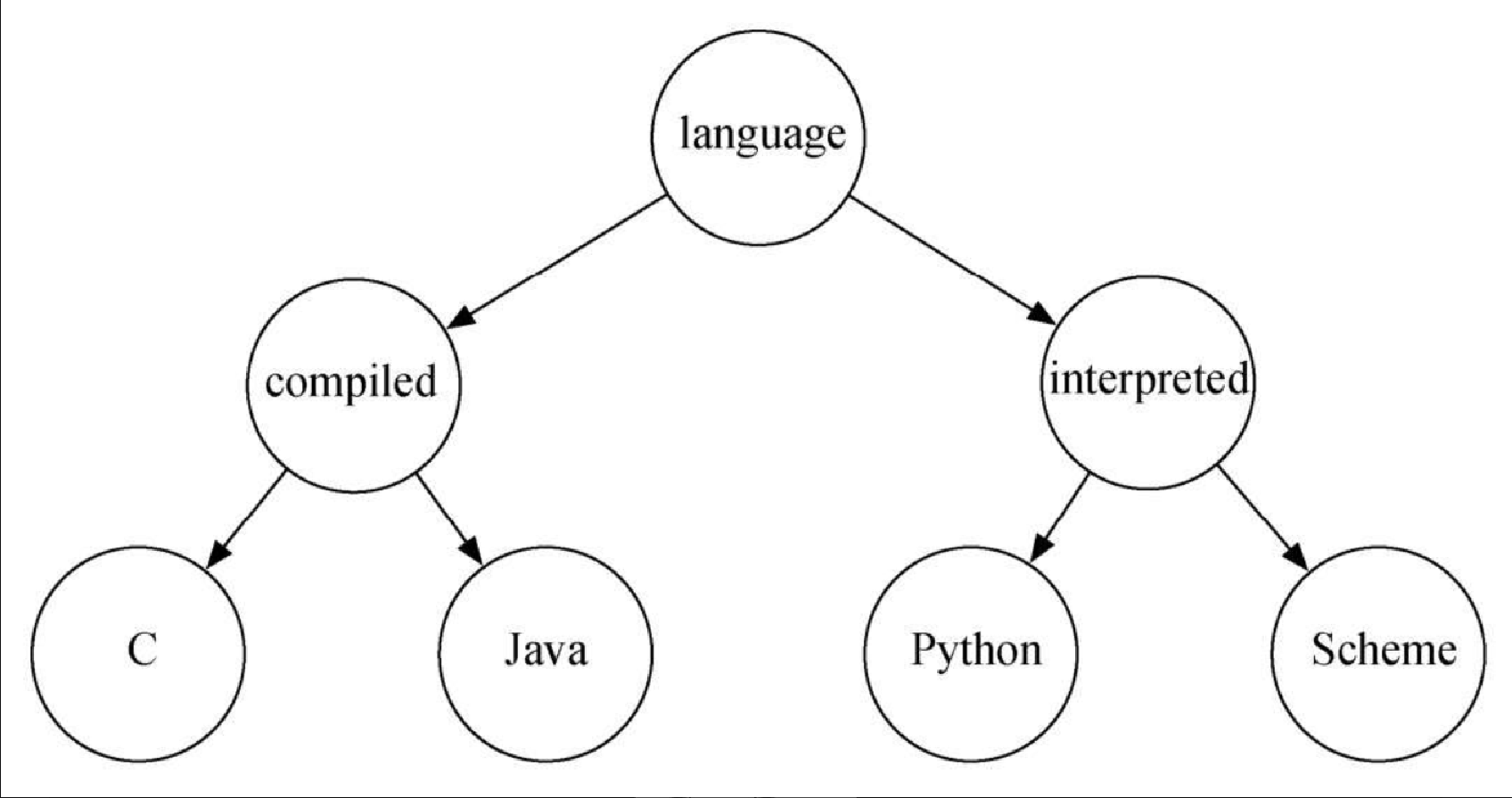
    image 2023 12 13 21 57 31 174

  13. 对下面这棵树，实施恢复平衡所需的旋转操作。

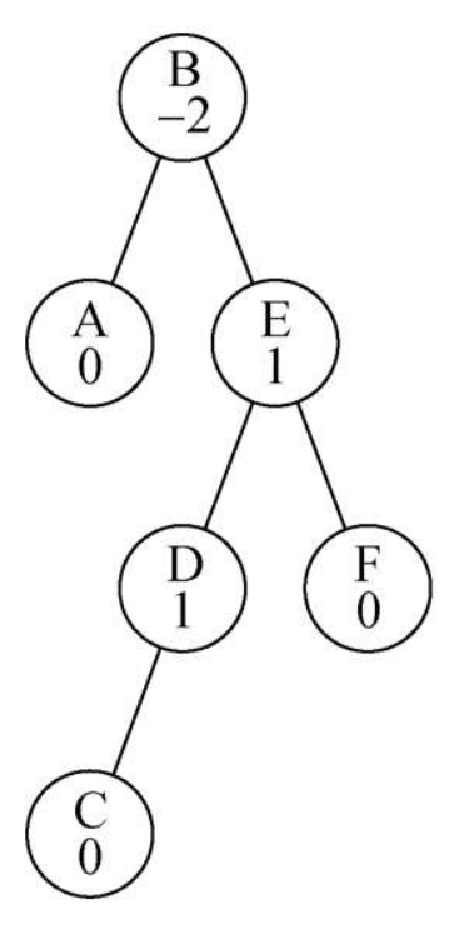
    image 2023 12 13 21 58 01 769

  14. 以图 6-30 作为出发点，推导出节点 D 在更新后的平衡因子等式。

编程练习

  1. 扩展 buildParseTree 方法，使其能处理字符间没有空格的数学表达式。

  2. 修改 buildParseTree 和 evaluate，使它们支持逻辑运算符（and、or、not）。注意，not 是一元运算符，这会让代码有点复杂。

  3. 使用 findSuccessor 方法，写一个非递归的二叉搜索树中序遍历方法。

  4. 修改二叉搜索树的实现代码，从而实现线索二叉搜索树。为线索二叉搜索树写一个非递归的中序遍历方法。线索二叉搜索树为其中的每个节点都维护着指向后继节点的引用。

  5. 修改二叉搜索树的实现代码，以正确处理重复的键。也就是说，如果键已在树中，就替换有效载荷，而不是用同一个键插入一个新节点。

  6. 创建限定大小的二叉堆。也就是说，堆只保持 n 个最重要的元素。如果堆的大小超过了 n，就会舍弃最不重要的元素。

  7. 整理 printexp 函数，去掉数字周围多余的括号。

  8. 使用 buildHeap 方法，针对列表写一个时间复杂度为 \$O(nlogn)\$ 的排序函数。

  9. 写一个函数，以数学表达式解析树为参数，计算各变量的导数。

  10. 将二叉堆实现为最大堆。

  11. 使用 BinaryHeap 类，实现一个叫作 PriorityQueue 的新类。为 PriorityQueue 类实现构造方法，以及 enqueue 方法和 dequeue 方法。

  12. 实现 AVL 树的 delete 方法。