拓扑排序
为了展示计算机科学家可以将几乎所有问题都转换成图问题,让我们来考虑如何制作一批松饼。配方十分简单:一个鸡蛋、一杯松饼粉、一勺油,以及 3/4 杯牛奶。为了制作松饼,需要加热平底锅,并将所有原材料混合后倒入锅中。当出现气泡时,将松饼翻面,继续煎至底部变成金黄色。在享用松饼之前,还会加热一些枫糖浆。图7-18 用图的形式展示了整个过程。
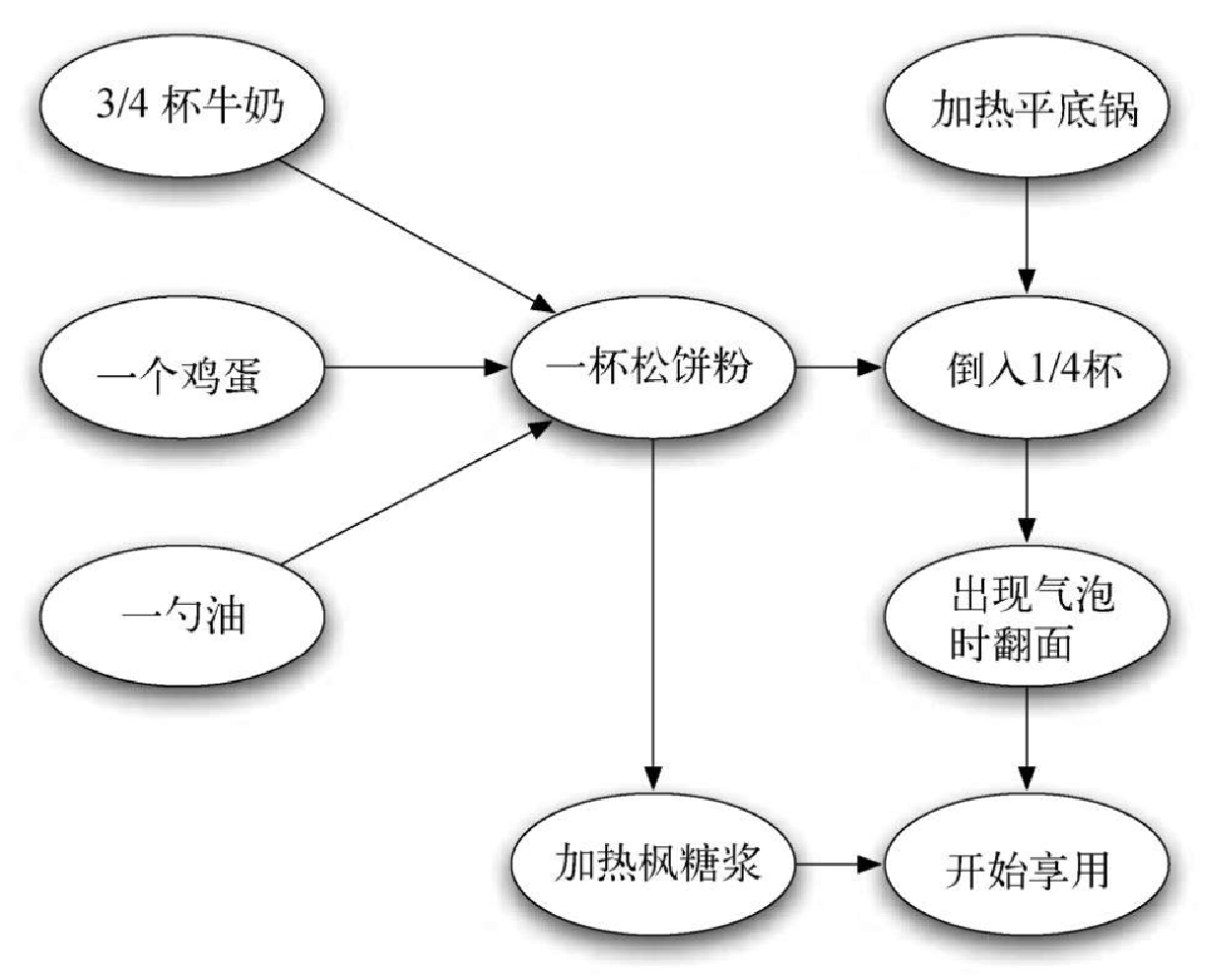
Figure 1. 图7-18 松饼的制作步骤
制作松饼的难点在于知道先做哪一步。从图7-18 可知,可以首先加热平底锅或者混合原材料。我们借助拓扑排序这种图算法来确定制作松饼的步骤。
拓扑排序根据有向无环图生成一个包含所有顶点的线性序列,使得如果图 G 中有一条边为 (v, w),那么顶点 v 排在顶点 w 之前。在很多应用中,有向无环图被用于表明事件优先级。制作松饼只是其中一个例子,其他例子还包括软件项目调度、优化数据库查询的优先级表,以及矩阵相乘。
拓扑排序是对深度优先搜索的一种简单而强大的改进,其算法如下。
-
对图 g调用 dfs(g)。之所以调用深度优先搜索函数,是因为要计算每一个顶点的结束时间。
-
基于结束时间,将顶点按照递减顺序存储在列表中。
-
将有序列表作为拓扑排序的结果返回。
图7-19 展示了 dfs 根据如图7-18 所示的松饼制作步骤构建的深度优先森林。
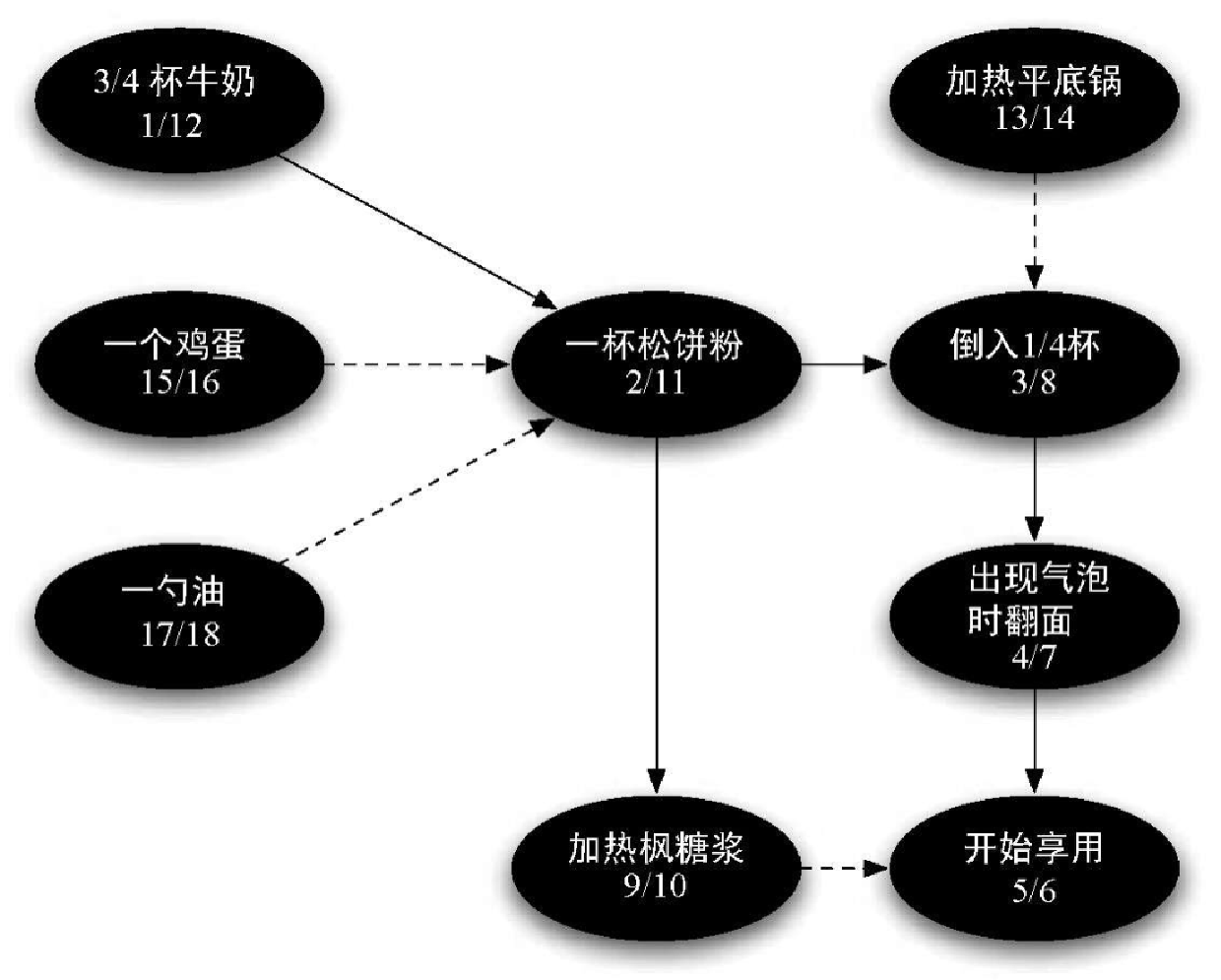
Figure 2. 图7-19 根据松饼制作步骤构建的深度优先森林
图7-20 展示了拓扑排序结果。现在,我们明确地知道了制作松饼所需的步骤。

Figure 3. 图7-20 对有向无环图的拓扑排序结果